Lecture Notes Week 4 Chapter 6 Methods 1





![Introduction to Methods Public static void main(String[]args) { System. out. println("Sum from 1 to Introduction to Methods Public static void main(String[]args) { System. out. println("Sum from 1 to](https://slidetodoc.com/presentation_image_h2/28a737eb1d55e8c626cb908698b19058/image-6.jpg)









![Pass by Value – an Example public class Increment { public static void main(String[] Pass by Value – an Example public class Increment { public static void main(String[]](https://slidetodoc.com/presentation_image_h2/28a737eb1d55e8c626cb908698b19058/image-19.jpg)








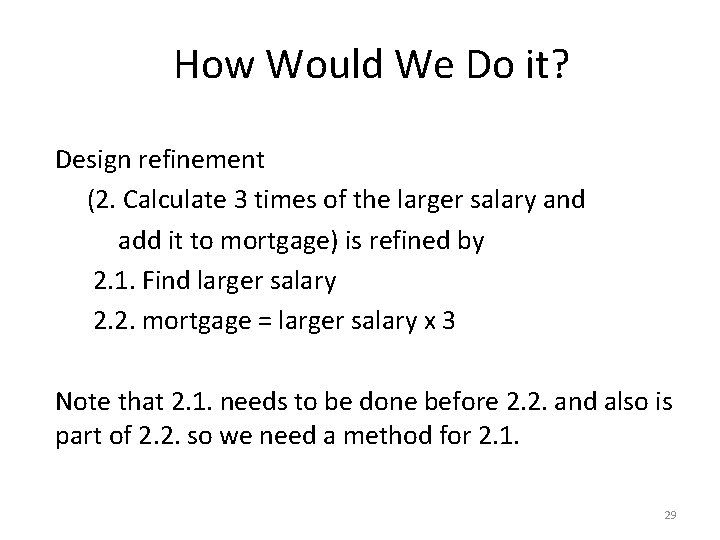











![Top-down Implementation – Top Level public class Prime. Number { public static void main(String[] Top-down Implementation – Top Level public class Prime. Number { public static void main(String[]](https://slidetodoc.com/presentation_image_h2/28a737eb1d55e8c626cb908698b19058/image-43.jpg)


- Slides: 45

Lecture Notes – Week 4 Chapter 6 (Methods) 1

Outline • • • Introduction to methods How to define and invoke methods Top-down design with methods Program structure charts Case studies To do list 2

Introduction to Methods • Motivating example: – Problem: Find the sums of integers from 1 to 10, from 20 to 30, and from 35 to 45, respectively. – How would we do it? – Intuitive solution: Write three loops for the three sums? – Better solution: Write a generalised program, called method, to do each of the three sums as specified? 3

Introduction to Methods int sum = 0; for (int i = 1; i <= 10; i++) sum += i; System. out. println("Sum from 1 to 10 is " + sum); sum = 0; for (int i = 20; i <= 30; i++) sum += i; System. out. println("Sum from 20 to 30 is " + sum); sum = 0; for (int i = 35; i <= 45; i++) sum += i; System. out. println("Sum from 35 to 45 is " + sum); 4

Introduction to Methods int sum = 0; for (int i = 1; i <= 10; i++) sum += i; System. out. println("Sum from 1 to 10 is " + sum); sum = 0; for (int i = 20; i <= 30; i++) sum += i; System. out. println("Sum from 20 to 30 is " + sum); sum = 0; for (int i = 35; i <= 45; i++) sum += i; System. out. println("Sum from 35 to 45 is " + sum); 5
![Introduction to Methods Public static void mainStringargs System out printlnSum from 1 to Introduction to Methods Public static void main(String[]args) { System. out. println("Sum from 1 to](https://slidetodoc.com/presentation_image_h2/28a737eb1d55e8c626cb908698b19058/image-6.jpg)
Introduction to Methods Public static void main(String[]args) { System. out. println("Sum from 1 to 10 is " + sum(1, 10); System. out. println("Sum from 20 to 30 is " + sum(20, 30); System. out. println("Sum from 35 to 45 is " + sum(35, 45); } public static int sum(int i 1, int i 2) { int sum = 0; for (int i = i 1; i <= i 2; i++) sum += i; return sum; } 6

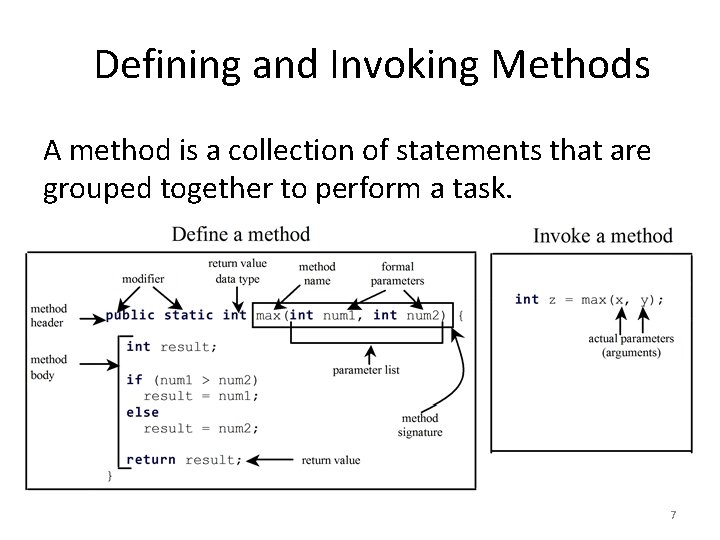
Defining and Invoking Methods A method is a collection of statements that are grouped together to perform a task. 7

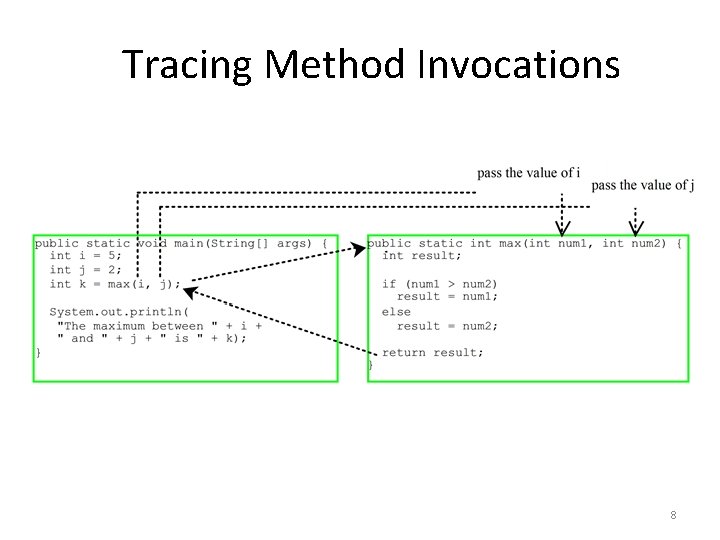
Tracing Method Invocations 8

Tracing Method Invocations i is now 5 9

Tracing Method Invocations j is now 2 10

Tracing Method Invocations Invoke max(i, j) 11

Tracing Method Invocations Invoke max(i, j) Pass the value of i to num 1 and Pass the value of j to num 2 12

Tracing Method Invocations (num 1 > num 2) is true since num 1 is 5 and num 2 is 2 13

Tracing Method Invocations result is 5. 14

Tracing Method Invocations Return the value of result, 5. 15

Tracing Method Invocations Return the value of the method invocation, 5, and assign it to k. 16

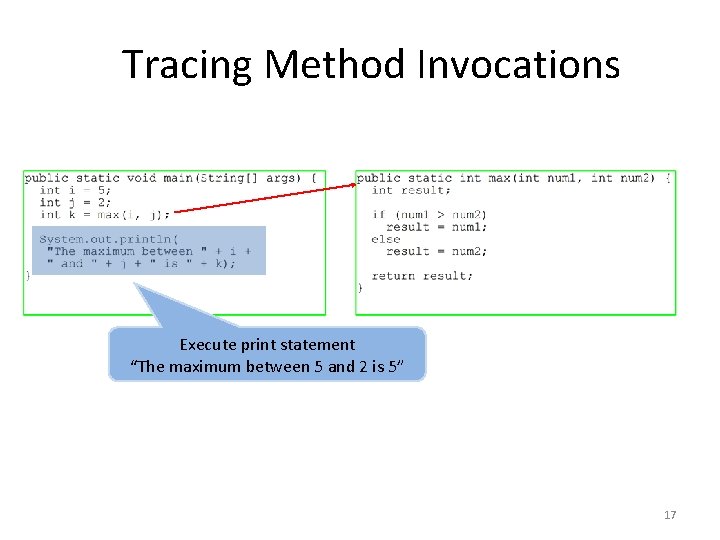
Tracing Method Invocations Execute print statement “The maximum between 5 and 2 is 5” 17

Pass by Value • When a method is invoked with an argument, the value of the argument is passed to the parameter. This is referred to as pass-byvalue. • If the argument is a variable, the value of the variable is passed to the parameter. The variable itself is not affected, regardless of the changes made to the parameter inside the method. 18
![Pass by Value an Example public class Increment public static void mainString Pass by Value – an Example public class Increment { public static void main(String[]](https://slidetodoc.com/presentation_image_h2/28a737eb1d55e8c626cb908698b19058/image-19.jpg)
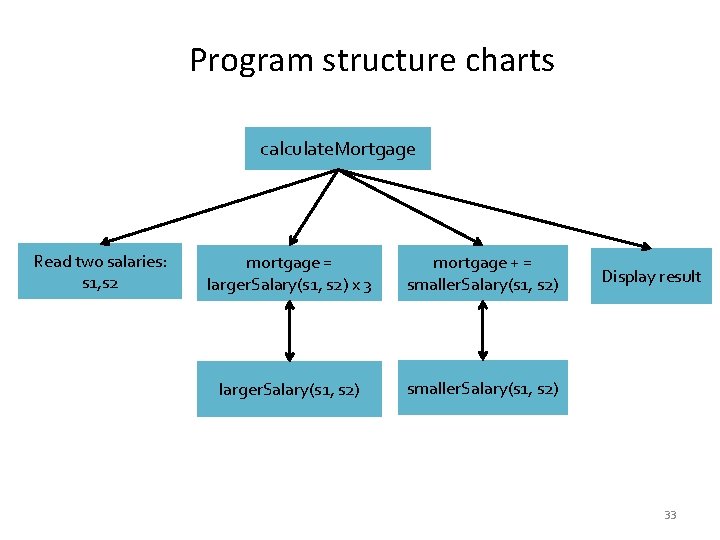
Pass by Value – an Example public class Increment { public static void main(String[] args) { int x = 1; System. out. println("Before the call, x is " + x); increment(x); System. out. println("After the call, x is " + x); } public static void increment(int n) { n++; System. out. println("n inside the method is " + n); } } 19

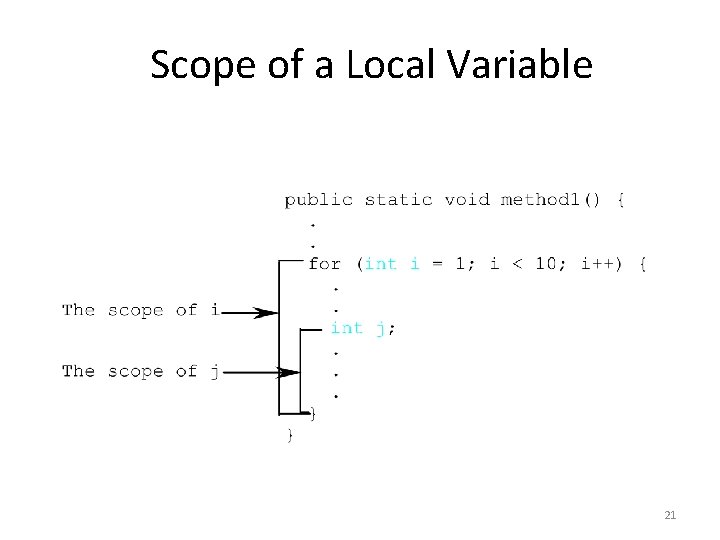
Scope of a Local Variable • Local variables: those defined within a method. • Scope of a local variable – starting from its declaration and until the end of the program block that contains the variable. • Local variables must be declared in a method before they are used in the method. 20

Scope of a Local Variable 21

Scope of a Local Variable 22

Scope of a Local Variable // Fine with no errors public static void correct. Method() { int x = 1; int y = 1; // i is declared for (int i = 1; i < 10; i++) { x += i; } // i is declared again for (int i = 1; i < 10; i++) { y += i; } } 23

Scope of a Local Variable // With errors public static void incorrect. Method() { int x = 1; int y = 1; for (int i = 1; i < 10; i++) { int x = 0; x += i; } } 24

Benefits of Methods • Reuse – a defined method can be repeatedly used. • Information hiding – think of a method as a black box of which you don’t need to know the implementation details. • Complexity reduction – divide a complex problem into a set of simpler problems to be solved by a set of methods. 25

Case Study 1 – Calculate Mortgages In this case study, we learn: • how to design a solution for a given problem, • how to divide a problem into a set of simpler problems to be solved by a set of methods, and • how to write, compile, run and test a program to implement the designed solution. 26

Problem Specification • The problem is to design, implement, run and test a program that calculates the maximum size of mortgage that the bank will lead you and your partner. • Suppose that this generally equates to 3 times the larger salary plus 1 times the smaller salary. 27

How Would We Do it? Top-level design 1. Read in two salaries 2. Calculate 3 times of the larger salary and add it to mortgage 3. Calculate the smaller salary and add it to mortgage 4. Display mortgage 28
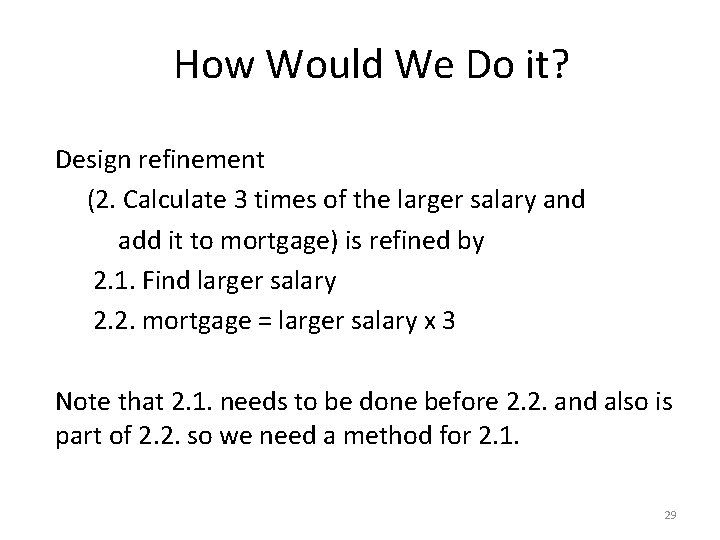
How Would We Do it? Design refinement (2. Calculate 3 times of the larger salary and add it to mortgage) is refined by 2. 1. Find larger salary 2. 2. mortgage = larger salary x 3 Note that 2. 1. needs to be done before 2. 2. and also is part of 2. 2. so we need a method for 2. 1. 29

How Would We Do it? Design refinement (2. 1. Find larger salary) is refined by 2. 1. 1. If (salary 1 > salary 2) Then 2. 1. 2 larger. Salary = salary 1 Else 2. 1. 3 larger. Salary = salary 2 30

How Would We Do it? Design refinement (3. Calculate the smaller salary and add it to mortgage) is refined by 3. 1. Find smaller salary 3. 2. mortgage = mortgage + smaller salary Note that 3. 1. needs to be done before 3. 2. and also is part of 3. 2. so we need a method for 3. 1. 31

How Would We Do it? Design refinement (3. 1. Find smaller salary) is refined by 3. 1. 1. If (salary 1 > salary 2) Then 3. 1. 2 smaller. Salary = salary 2 Else 3. 1. 3 smaller. Salary = salary 1 32

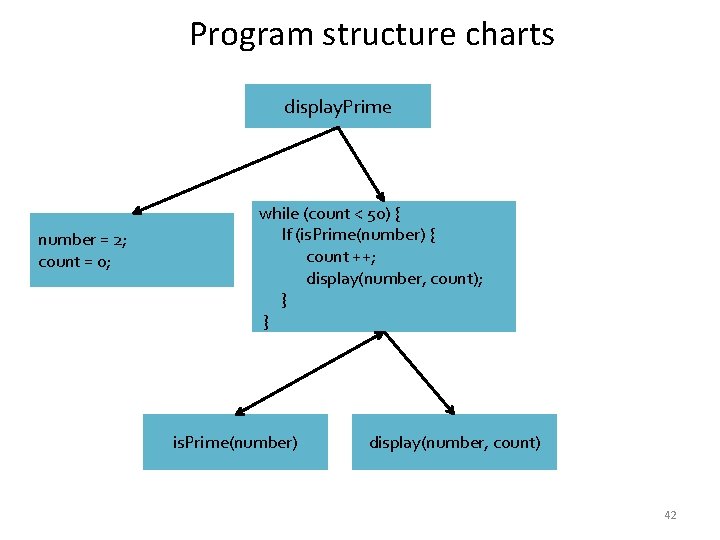
Program structure charts calculate. Mortgage Read two salaries: s 1, s 2 mortgage = larger. Salary(s 1, s 2) x 3 mortgage + = smaller. Salary(s 1, s 2) larger. Salary(s 1, s 2) smaller. Salary(s 1, s 2) Display result 33

Implementation with methods Implementation strategies: Given a program structure chart, how do we implement it? • Top-down strategy – start with the top level program with method stubs and gradually replace these method stubs with complte ones level by level • Bottom-up strategy – start with the methods on the bottom level and gradually move up to higher level methods and eventually top-level main method. 34

Top-down implementation – top level /* This program calculates a mortgage. */ import java. util. Scanner; public class Calculate. Mortgage { public static void main(String[] args) { Scanner input = new Scanner(system. in); double salary 1, salary 2, mortgage; // Read in two salaries, salary 1, salary 2 System. out. print("Enter two salaries separated by a space: "); double salary 1 = input. next. Double(); double salary 2 = input. next. Double(); // Calculate mortgage = larger. Salary(Salary 1, Salary 2) * 3; mortgage += smaller. Salary(Salary 1, Slary 2); System. out. println(”The maximum size of mortgage is: ” + mortgage); public static double larger. Salary(double salary 1, double salary 2) { return 1; // method stub } public static double smaller. Salary(double salary 1, double salary 2) { return 1; // method stub } 35

Top-down implementation – with method implementations public static double larger. Salary(double salary 1, double salary 2) { if (salary 1 > salary 2) return salary 1; else return salary 2; } public static double smaller. Salary(double salary 1, double salary 2) { if (salary 1 > salary 2) return salary 2; else return salary 1; } Note: Those method stubs will now need to be replaced by these complete method implementations. 36

Bottom-up implementation – with bottomlevel implementations /* This program calculates a mortgage. */ public class Calculate. Mortgage { public static void main(String[] args) { double larger = larger. Salary(1, 2); double smaller = smaller. Salary(1, 2); System. out. println(”The larger and smaller are: ” + larger + smaller); } public static double larger. Salary(double salary 1, double salary 2) { if (salary 1 > salary 2) return salary 1; else return salary 2; } public static double smaller. Salary(double salary 1, double salary 2) { if (salary 1 > salary 2) return salary 2; else return salary 1; } } 37

Case Study 2 – Displaying Prime Numbers with Methods • The problem: Display the first fifty prime numbers in five lines, each containing ten numbers. 38

Algorithm Design - Pseudocode 1. Set count to 0; 2. Set number to 2; 3. While count < 50 { 3. 1. Find if is. Prime(number) is true 3. 2. If is. Prime(number) { 3. 2. 1. Increment count by 1; 3. 2. 2. display(number, count); } 3. 3. Increment number by 1; } 39

Algorithm Refinement with Methods (find if Is. Prime(number) is true) is refined by 3. 1. 1. Set is. Prime to true; 3. 1. 2. for divisor = 2 to number/2 { if (number % divisor == 0) { Set is. Prime to false; Exit the loop; } } 40

Algorithm Refinement with Methods (3. 2. 2. display(number, count)) is refined by 3. 2. 2. 1. if (count % 10 == 0) { Display number and new line; else Display number; 41

Program structure charts display. Prime number = 2; count = 0; while (count < 50) { If (is. Prime(number) { count ++; display(number, count); } } is. Prime(number) display(number, count) 42
![Topdown Implementation Top Level public class Prime Number public static void mainString Top-down Implementation – Top Level public class Prime. Number { public static void main(String[]](https://slidetodoc.com/presentation_image_h2/28a737eb1d55e8c626cb908698b19058/image-43.jpg)
Top-down Implementation – Top Level public class Prime. Number { public static void main(String[] args) { int count = 0; // number of primes so far int number = 2; // A number to be tested System. out. println("The first 50 prime numbers are n"); // Repeatedly find prime numbers while (count < 50) { if (is. Prime(number)) { count++; // Increase the count display. Prime(number, count); } number++; // Check if the next number is prime } } public static boolean is. Prime(int number) { return true; // stub } public static void display. Prime(int number, int count) { } // stub } 43

Top-down Implementation with Method Implementations // Test whether number is prime public static boolean is. Prime(int number) { boolean is. Prime = true; for (int divisor = 2; divisor <= number / 2; divisor++) { if (number % divisor == 0) { // If true, not prime is. Prime = false; // number is not a prime break; // Exit the for loop – no further test } } return is. Prime; } // Display a prime public static void display. Prime(int number, int count) { if (count % 10 == 0) { // Display the number and advance to the new line System. out. println(number); } else System. out. print(number + " "); } 44

To Do List Before Next Lectures • Read Week 4 lecture slides. • Read and run Week 4 program examples. • Selectively read those sections in Chapter 6 that cover the topics in this lecture. • Attend your practical session in Week 5. • Glance through those sections in Chapters 7 and 8 that cover the topics in Week 5’s lecture. 45