Lecture for M Sc Bioinformatics Sem2 nd Course

Lecture for M. Sc. Bioinformatics Sem-2 nd Course code: MSBIS 2002 C 04 Course Name: Biomolecular Modelling and simulation

Outline of the lecture v v v v v Neighbor list PBC(Periodic Boundary Condition) Constraints MD steps Time step And practical aspects of MD And remaining topics Topology Water maodel Membrane model CARMM GUI etc

Periodic Boundary condition • Computing the non bonded contribution to the interatomic forces in an MD simulation involves large number of pair wise calculations. • We Consider each atom i interact all other atoms j • Let us assume that the interaction potential are of short range, v(rij)=0 if rij >rcut, the potential cutoff. • In this case, the programme skips the force calculations and considers the next candidate j. • Time to examine all pair separations is proportional to the number of distinct pairs, 1/2 N(N-1) in an N atom System, and for every pair must compute at least r 2 ij; this still consume lot of time

• Verlet suggested a technique for improving the speed of programme that is the use of lists of nearby pairs of atoms. • The potential cutoff sphere, of radius of rcut, around particular atom surrounded by a definite boundary, to give a larger sphere of radius rlist as in figure. • At the first step of simulation a list is constructed of all the neighbors of each atom, for which the pair separations is within rlist. • Over the next few MD steps, only pairs appearing in the list are checked in the force routine.

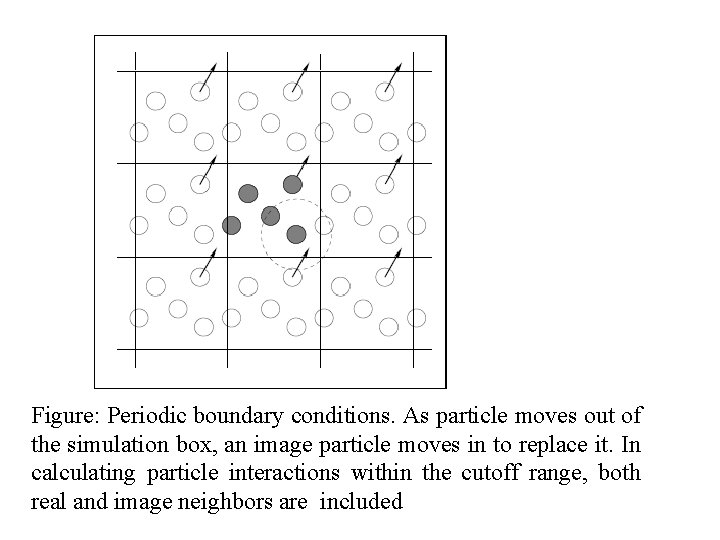
Figure: Periodic boundary conditions. As particle moves out of the simulation box, an image particle moves in to replace it. In calculating particle interactions within the cutoff range, both real and image neighbors are included

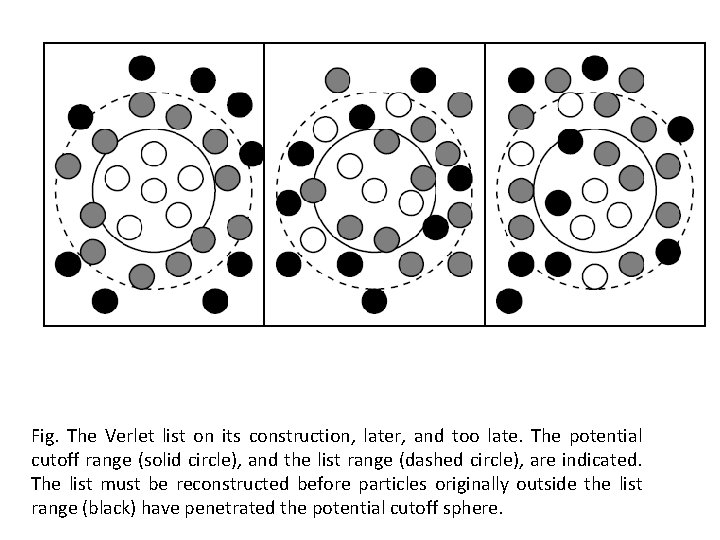
Fig. The Verlet list on its construction, later, and too late. The potential cutoff range (solid circle), and the list range (dashed circle), are indicated. The list must be reconstructed before particles originally outside the list range (black) have penetrated the potential cutoff sphere.

v Time to time the list is reconstructed: it is important to do this before any unlisted pairs have crossed the safety zone and come within interaction range. v It is possible to trigger the list reconstruction automatically, if a record is kept of the distance travelled by each atom since the last update. v The choice of list cutoff distance rlist is a compromise: larger lists will need to be reconstructed less frequently, but will not give as much of a saving on cpu time as smaller lists. This choice can easily be made by experimentation.

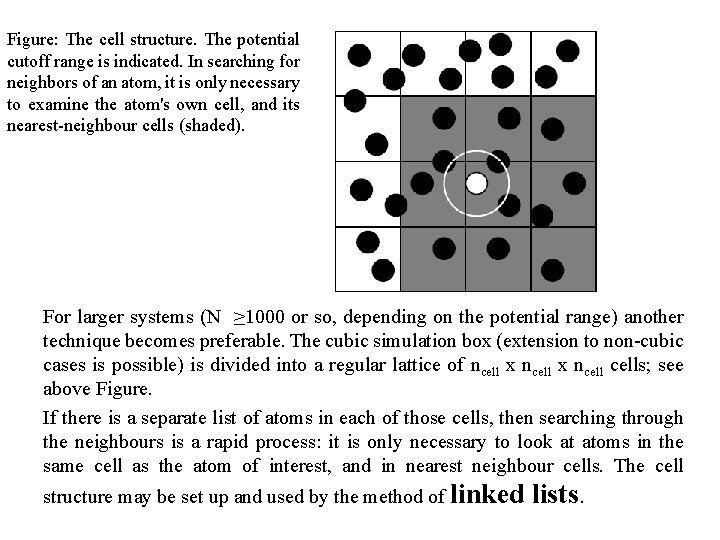
Figure: The cell structure. The potential cutoff range is indicated. In searching for neighbors of an atom, it is only necessary to examine the atom's own cell, and its nearest-neighbour cells (shaded). For larger systems (N ≥ 1000 or so, depending on the potential range) another technique becomes preferable. The cubic simulation box (extension to non-cubic cases is possible) is divided into a regular lattice of ncell x ncells; see above Figure. If there is a separate list of atoms in each of those cells, then searching through the neighbours is a rapid process: it is only necessary to look at atoms in the same cell as the atom of interest, and in nearest neighbour cells. The cell structure may be set up and used by the method of linked lists.

• The first part of the method involves sorting all the atoms into their appropriate cells. • This sorting is rapid, and may be performed every step. Then, within the force routine, pointers are used to scan through the contents of cells, and calculate pair forces. • This approach is very efficient for large systems with shortrange forces. • A certain amount of unnecessary work is done because the search region is cubic, not (as for the Verlet list) spherical.

MD further comments Constraints and shake • If certain motions are considered unimportant, constrained MD can be more efficient e. g. SAKE algorithm –bond length constraints • Rigid bodies can be used e. g. Eulers methods and quaternion algorithms

Key Stages in MD Simulation More Elaborated steps in Next Slide

• Remaining Topics will see you in Next Lecture