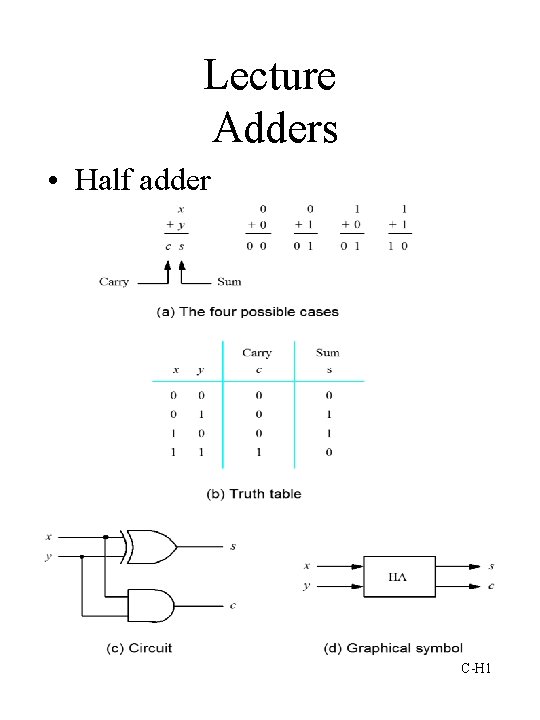
Lecture Adders Half adder CH 1 Full Adder

Lecture Adders • Half adder C-H 1

Full Adder si is the modulo 2 sum of ci, xi, yi. C-H 2

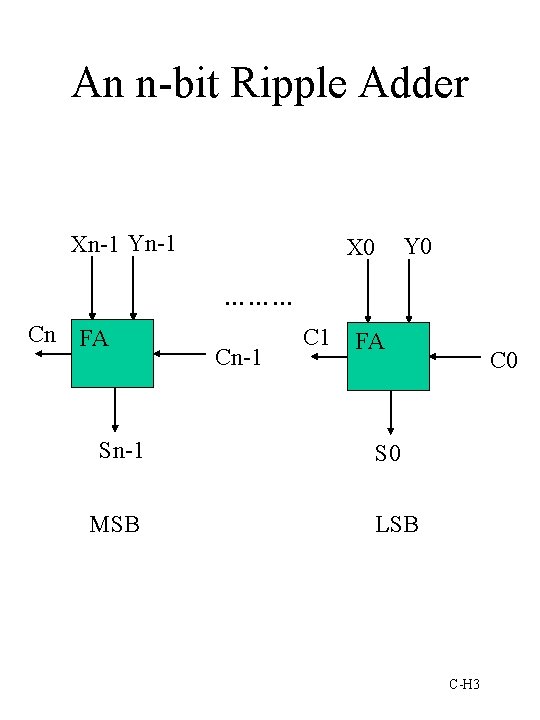
An n-bit Ripple Adder Xn-1 Yn-1 X 0 Y 0 ……… Cn FA Sn-1 MSB Cn-1 C 1 FA C 0 S 0 LSB C-H 3

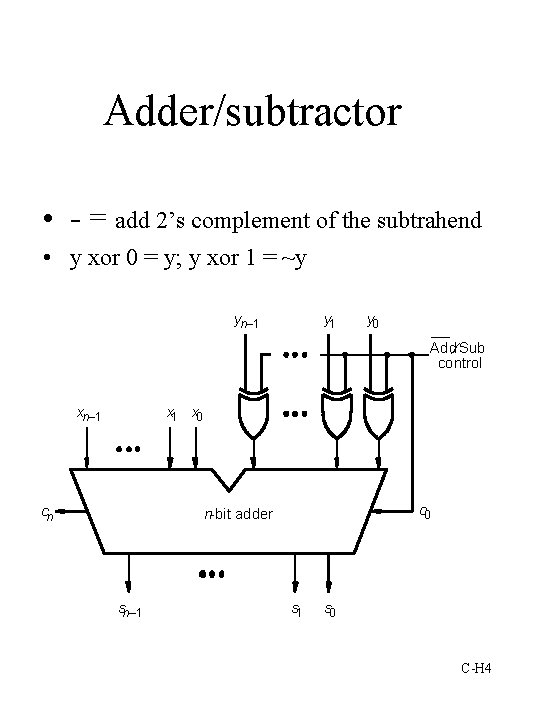
Adder/subtractor • - = add 2’s complement of the subtrahend • y xor 0 = y; y xor 1 = ~y yn– 1 y 0 Add¤ Sub control xn– 1 x 0 cn c 0 n-bit adder sn– 1 s 0 C-H 4

Overflow v. s. Carry-out • n-bit signed number: -2 n-1 to 2 n-1 -1 Detect overflow for signed number: Overflow = Cn-1 ⊕ Cn Overflow = Xn-1 Yn-1 ~Sn-1 (110) + ~Xn-1 ~Yn-1 Sn-1 (001) where X and Y represent the 2’s complement numbers, S = X+Y. (sign bits 0, 0 ≠ 1 ) 0111 1111 Carry-out: for unsigned number C-H 5

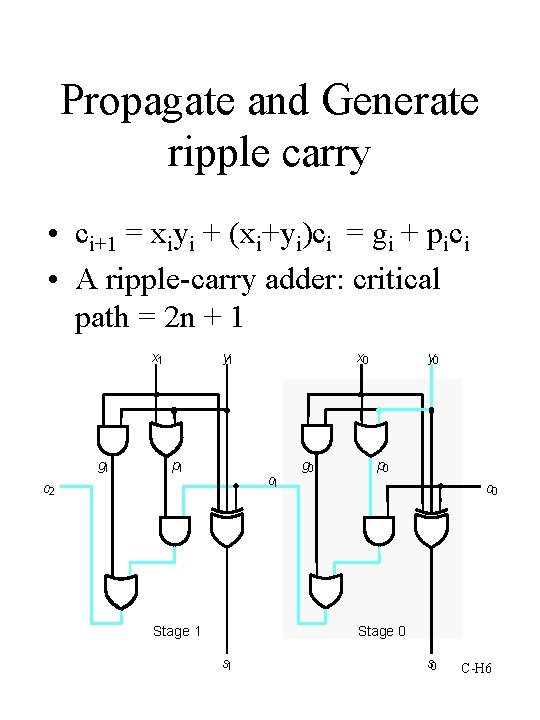
Propagate and Generate ripple carry • ci+1 = xiyi + (xi+yi)ci = gi + pici • A ripple-carry adder: critical path = 2 n + 1 x 1 g 1 y 1 p 1 x 0 c 1 c 2 Stage 1 g 0 y 0 p 0 c 0 Stage 0 s 1 s 0 C-H 6

Problem: ripple carry adder is slow

Carry-lookahead adder • Motivation: – If we didn't know the value of carry-in, what could we do? – When would we always generate a carry? gi is true. g i = a i bi – When would we propagate the carry? pi is true. pi = a i + b i ci+1 = (bi. ci)+(ai. ci) +(ai. bi) = (ai. bi) + (ai+ bi). ci c 2 = g 1 + p 1. c 1 c 3 = g 2 + p 2. c 2 c 4 is computed once inputs (a 0 -a 3, b 0 to b 3, and c 0) are valid.

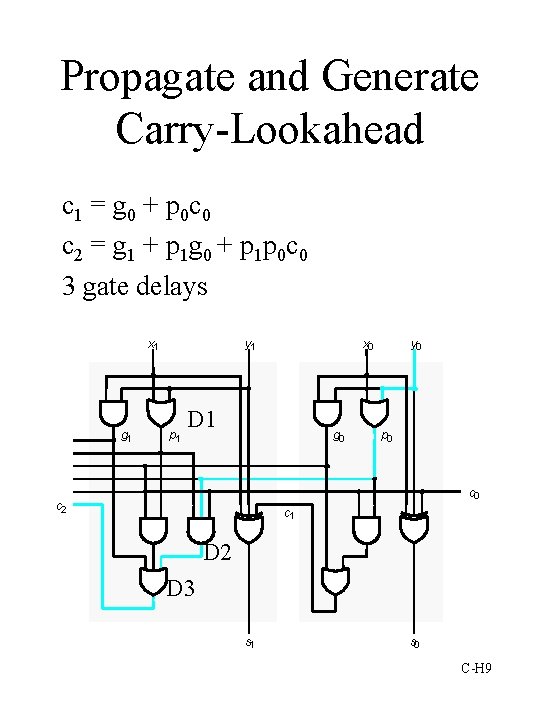
Propagate and Generate Carry-Lookahead c 1 = g 0 + p 0 c 0 c 2 = g 1 + p 1 g 0 + p 1 p 0 c 0 3 gate delays x 1 y 1 x 0 g 1 p 1 D 1 y 0 g 0 p 0 c 2 c 1 D 2 D 3 s 1 s 0 C-H 9

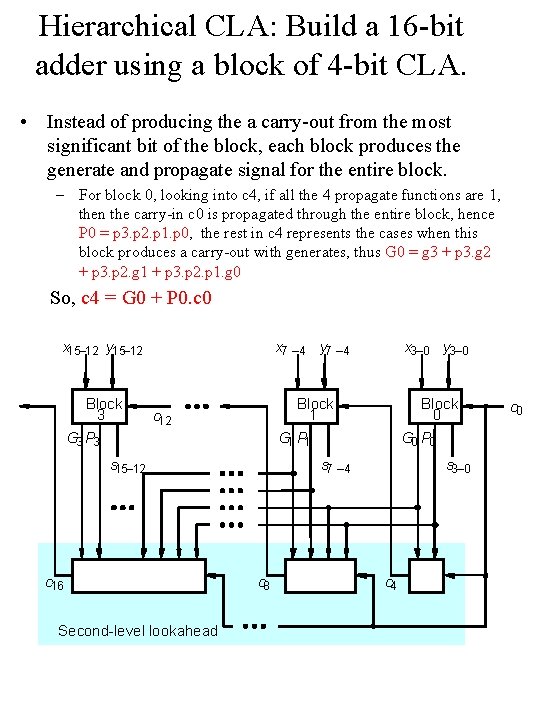
Hierarchical CLA: Build a 16 -bit adder using a block of 4 -bit CLA. • Instead of producing the a carry-out from the most significant bit of the block, each block produces the generate and propagate signal for the entire block. – For block 0, looking into c 4, if all the 4 propagate functions are 1, then the carry-in c 0 is propagated through the entire block, hence P 0 = p 3. p 2. p 1. p 0, the rest in c 4 represents the cases when this block produces a carry-out with generates, thus G 0 = g 3 + p 3. g 2 + p 3. p 2. g 1 + p 3. p 2. p 1. g 0 So, c 4 = G 0 + P 0. c 0 x 15– 12 y 15– 12 Block 3 c 12 G 3 P 3 x 7 – 4 y 7 – 4 x 3– 0 y 3– 0 Block 1 Block 0 G 1 P 1 s 15– 12 c 16 Second-level lookahead G 0 P 0 s 7 – 4 c 8 s 3– 0 c 4 c 0

Second Level Equation • • The same principle as in the first level is used in the second level. The result of the second level is computed as soon as its inputs are valid. c 4 = G 0 + (P 0. c 0) c 8 = G 1 + (P 1. G 0) + (P 1. P 0. c 0) c 12 = G 2 + (P 2. G 1) + (P 2. P 1. G 0) +(P 2. P 1. P 0. c 0) c 16 = G 3 + (P 3. G 2) +(P 3. P 2. G 1) + (P 3. P 2. P 1. G 0) +(P 3. P 2. P 1. P 0. c 0) In block 0

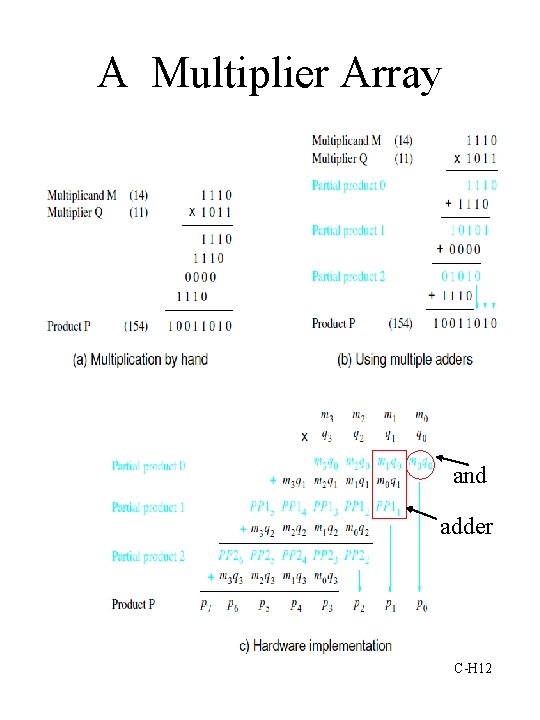
A Multiplier Array and adder C-H 12

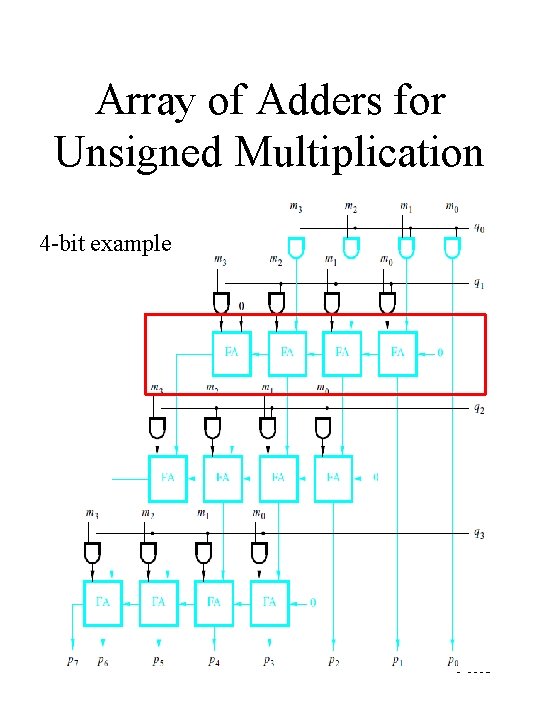
Array of Adders for Unsigned Multiplication 4 -bit example C-H 13