Lecture 9 Structure for DiscreteTime System XILIANG LUO

Lecture 9: Structure for Discrete-Time System XILIANG LUO 2014/11 1

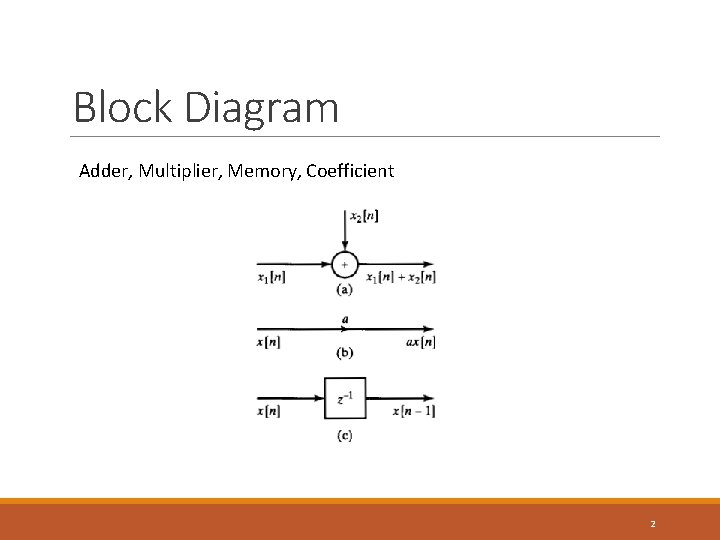
Block Diagram Adder, Multiplier, Memory, Coefficient 2

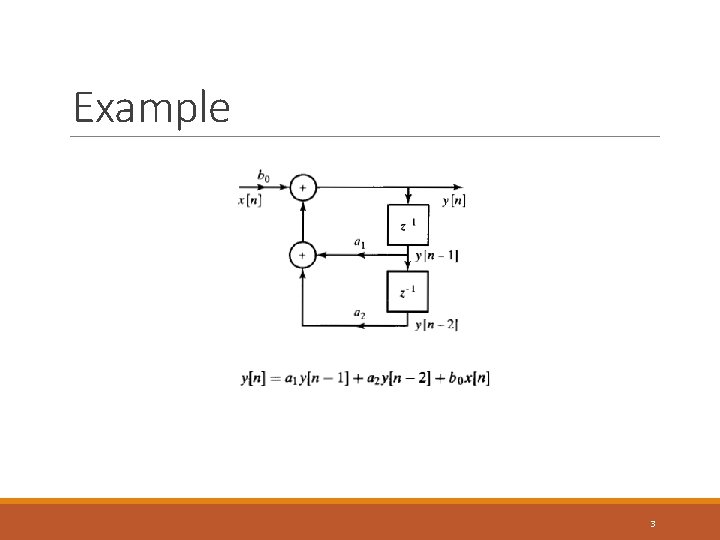
Example 3

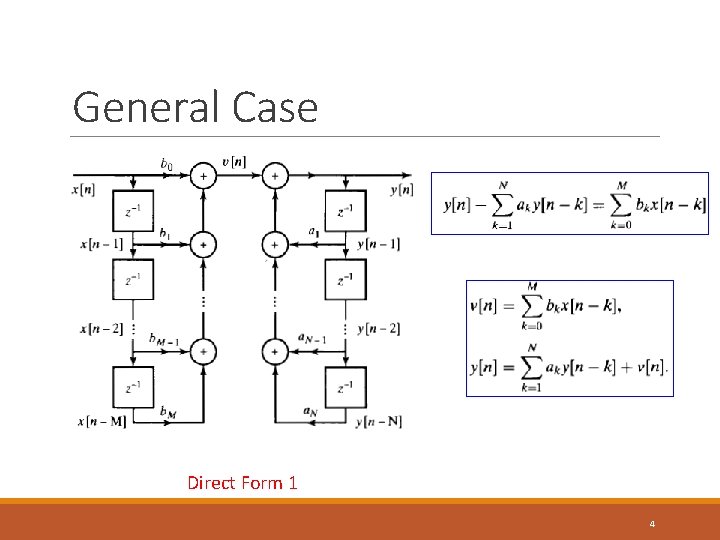
General Case Direct Form 1 4

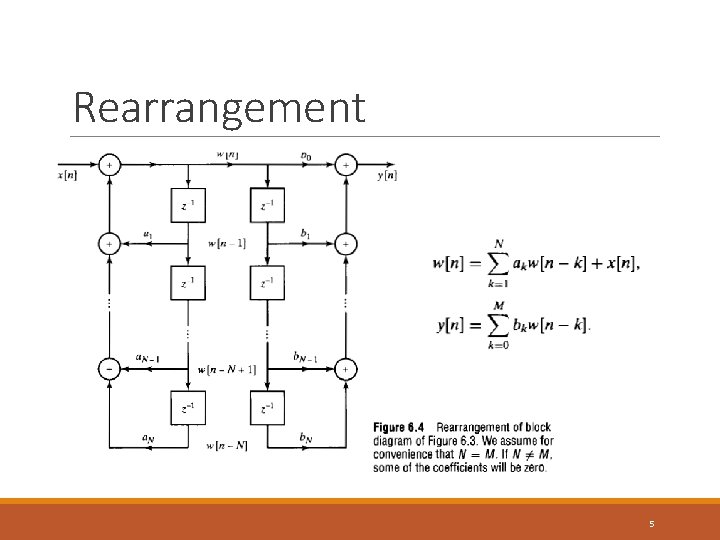
Rearrangement 5

Rearrangement Zeros 1 st Poles 1 st 6

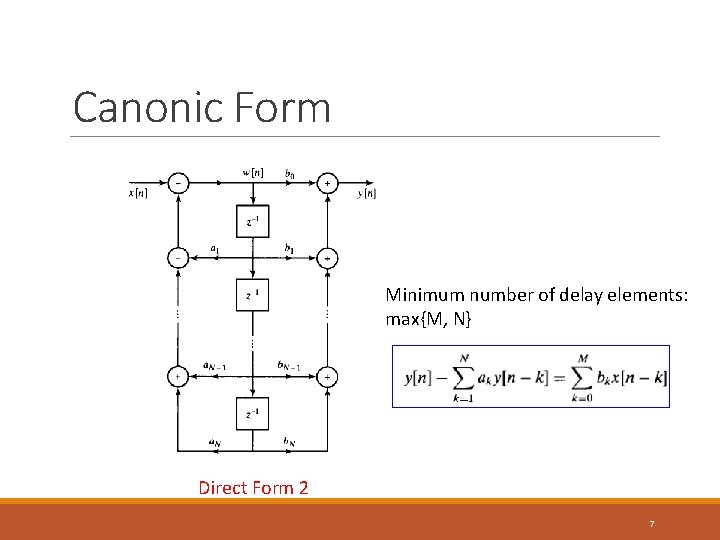
Canonic Form Minimum number of delay elements: max{M, N} Direct Form 2 7

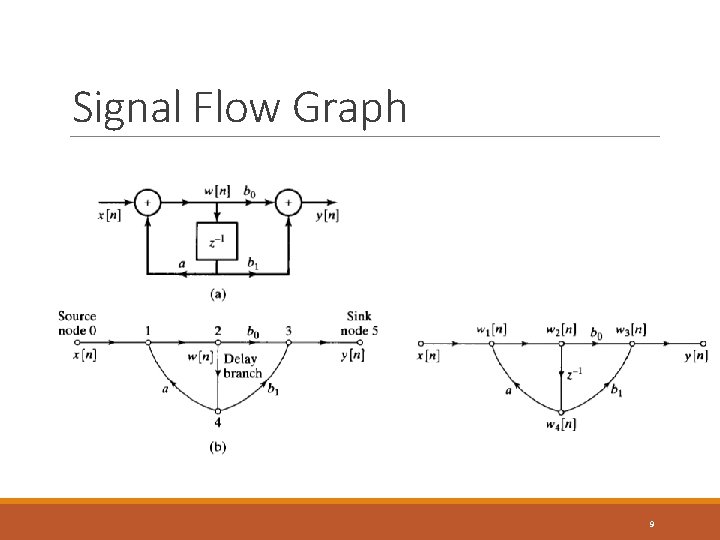
Signal Flow Graph A directed graph with each node being a variable or a node value. The value at each node in a graph is the sum of the outputs of all the branches entering the node. Source node: no entering branches Sink node: no outputs 8

Signal Flow Graph 9

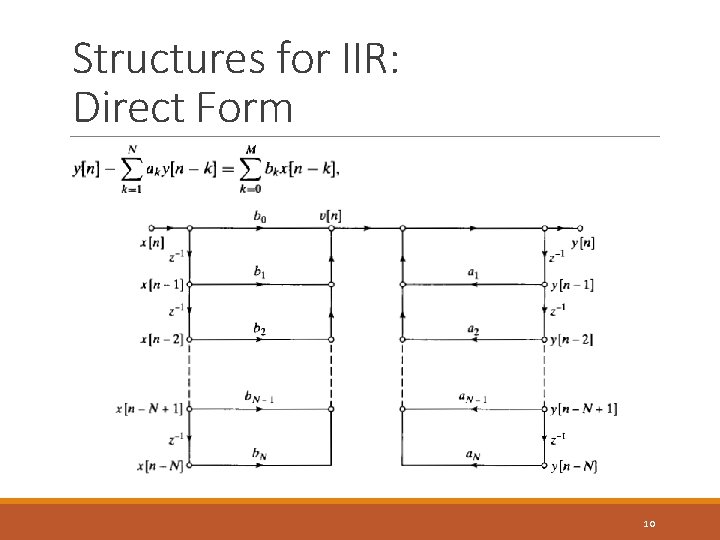
Structures for IIR: Direct Form 10

Structures for IIR: Direct Form 11

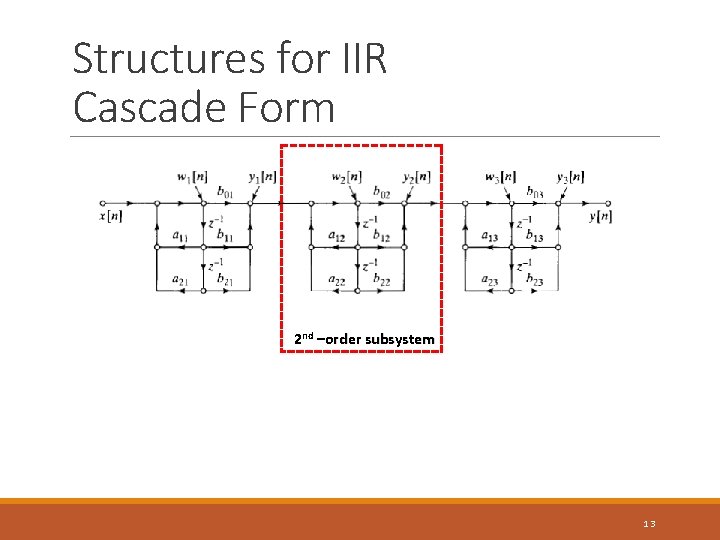
Structures for IIR: Cascade Form Real coefs: Combine pairs of real factors/ complex conjugate pairs 12

Structures for IIR Cascade Form 2 nd –order subsystem 13

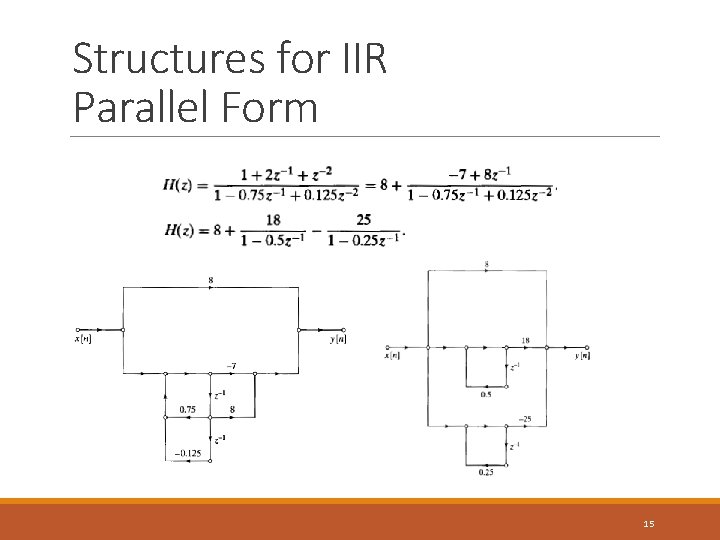
Structures for IIR Parallel Form Partial fraction expansion: Group real poles in pairs: 14

Structures for IIR Parallel Form 15

Feedback Loops Loop: closed path starting at a node and returning to same node by traversing branches in the direction allowed, which is defined by the arrowheads If a network has no loops, then the system function has only zeros and the impulse response has finite duration! Loops are necessary to generate infinitely long impulse responses! input unit impulse, the output is: 16

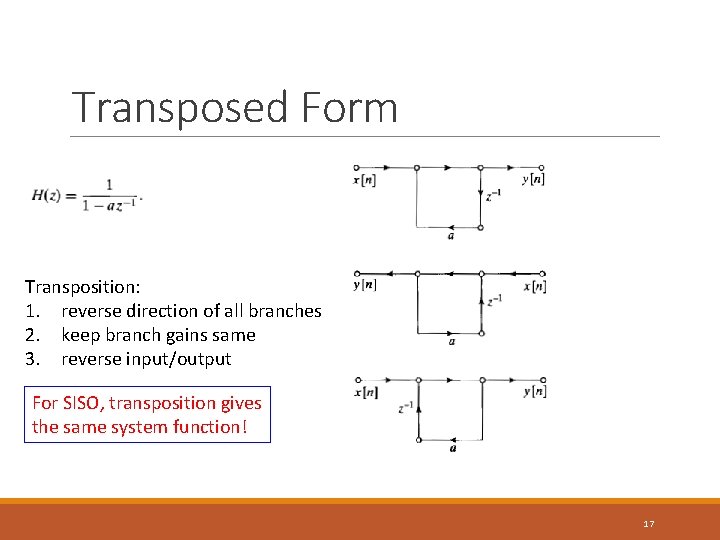
Transposed Form Transposition: 1. reverse direction of all branches 2. keep branch gains same 3. reverse input/output For SISO, transposition gives the same system function! 17

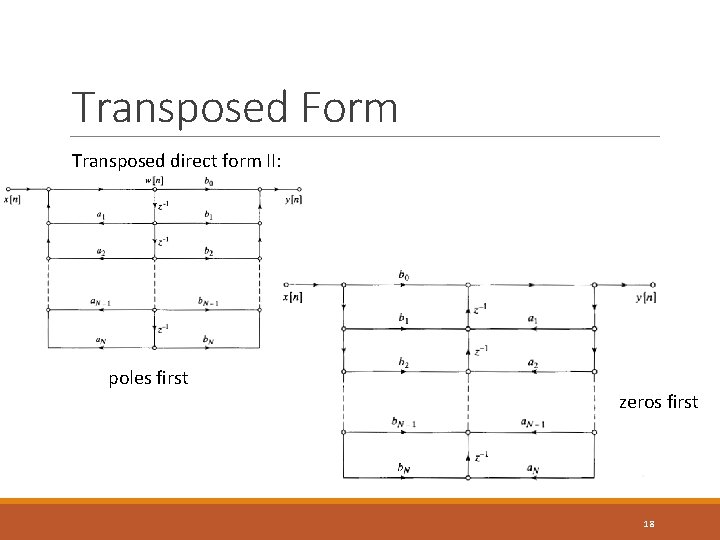
Transposed Form Transposed direct form II: poles first zeros first 18

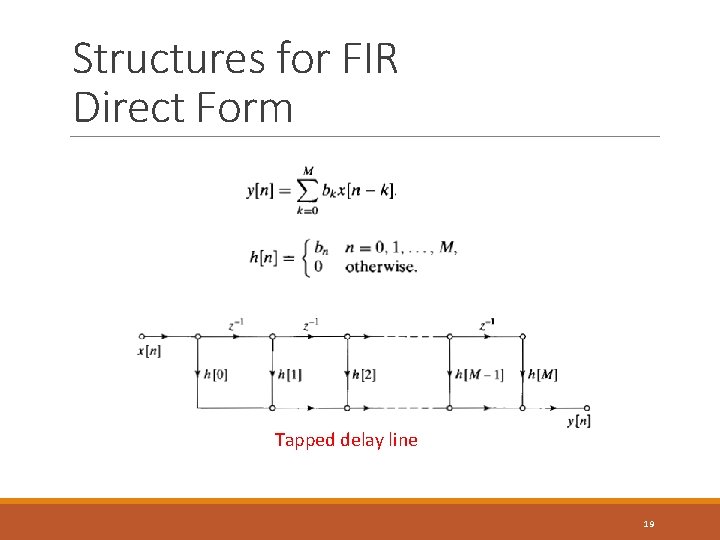
Structures for FIR Direct Form Tapped delay line 19

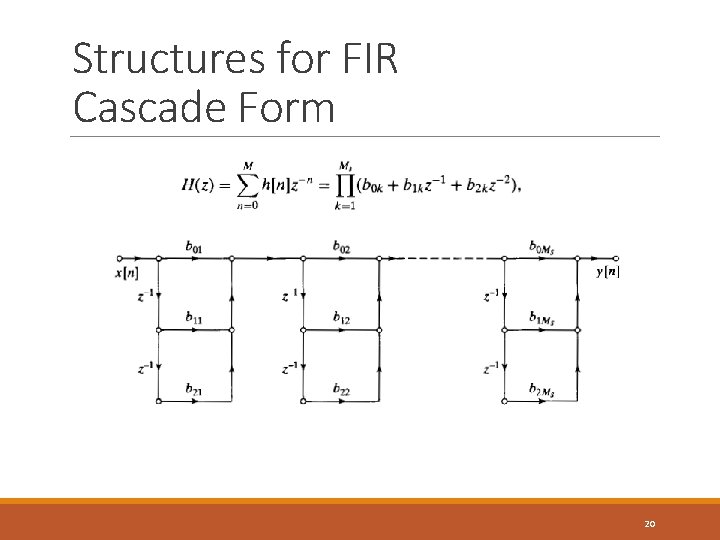
Structures for FIR Cascade Form 20

Structures for FIR with Linear Phase Impulse response satisfies the following symmetry condition: or So, the number of coefficient multipliers can be essentially halved! Type-1: 21

Lattice Filters 2 -port flow graph 22

Lattice Filters: FIR 23

Lattice Filters: FIR Input to i-th nodes: Recursive computation of transfer functions! 24

Lattice Filters: FIR To obtain a direct recursive relationship for the coefficients, or the impulse response, we use the following definition: 25

Lattice Filters: FIR From k-parameters to FIR impulse response: 26

Lattice Filters: FIR From FIR impulse response to k-parameters: 27

Lattice Filters: FIR From FIR impulse response to k-parameters: 28

Lattice Filters: FIR Direct Form Lattice Form 29

Lattice Filters: IIR Invert the computations in the following figure: 30

Lattice Filters: IIR Derive from FIR: IIR: 31

Lattice Filters: IIR Derive from 32

Lattice Filters: IIR 33