Lecture 9 Recursive Programming Hanoi Tower Solving Prefix

Lecture 9 Recursive Programming Hanoi Tower Solving Prefix expression evaluation 軟體實作與計算實驗 1

Multiple Stacks Hanoi Tower Play Panel 軟體實作與計算實驗 2

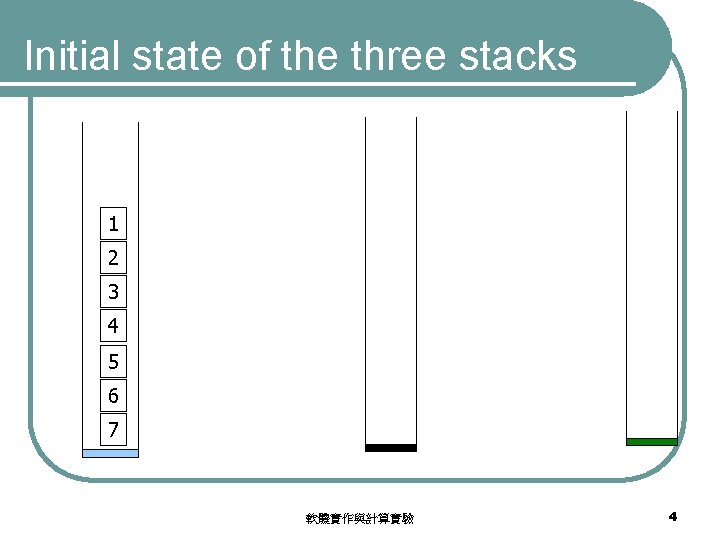
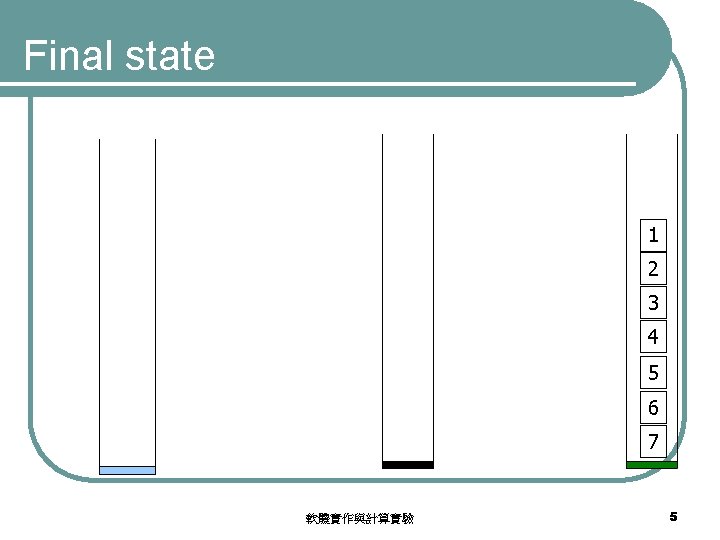
Problem statement l Three stacks l The first stack contains n disks, numbered from 1, …, n l Move all disks from the first stack to the third stack. l A disk is never on the top of a smaller disk 軟體實作與計算實驗 3

Initial state of the three stacks 1 2 3 4 5 6 7 軟體實作與計算實驗 4

Final state 1 2 3 4 5 6 7 軟體實作與計算實驗 5

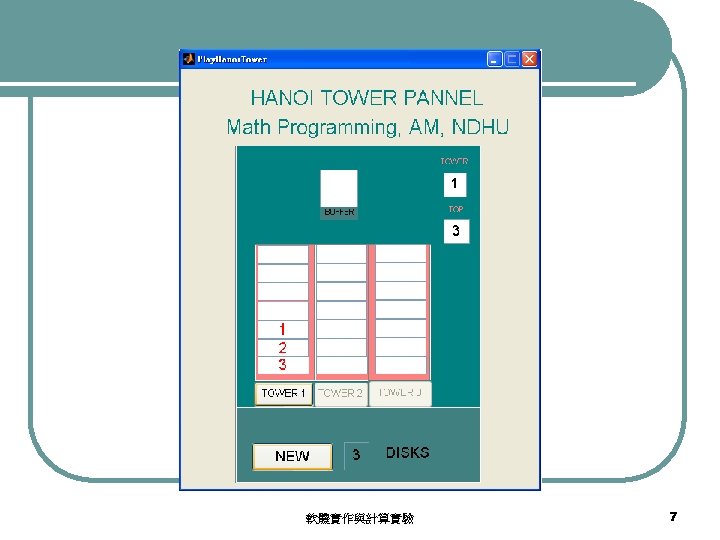
A Hanoi Tower Panel Play. Hanoi. Tower. rar 軟體實作與計算實驗 6

Three steps for auto-play Move n-1 objects from stack 1 to stack 2 l Move 1 object from stack 1 to stack 3 l Move n-1 objects from stack 2 to stack 3 l 軟體實作與計算實驗 8

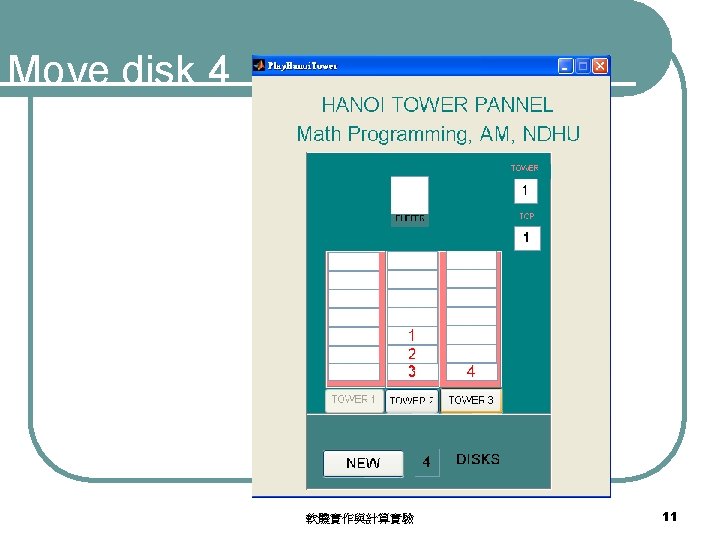
Initial state of 4 -disk problem 軟體實作與計算實驗 9

Move 3 disks from stack 1 to 2 軟體實作與計算實驗 10

Move 3 disks from stack 2 to 3 軟體實作與計算實驗 12

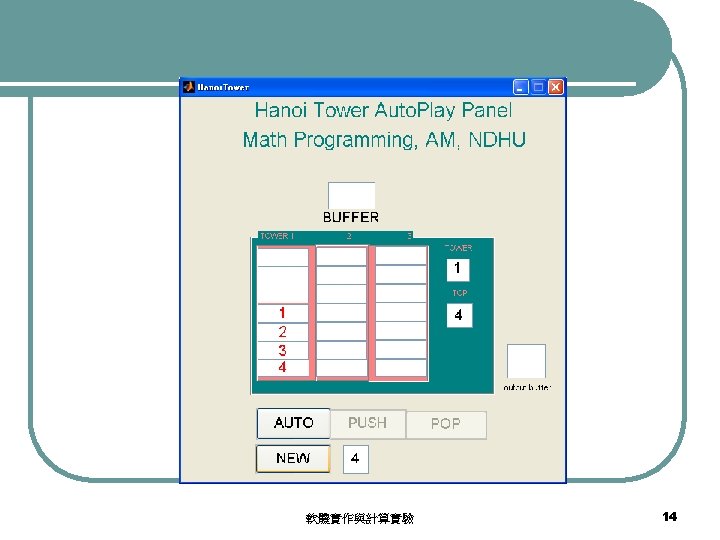
Hanoi-tower auto-play panel Hanoi. Tower. rar 軟體實作與計算實驗 13

Hanoi Tower Play Panel Play. Hanoi. Tower. rar 軟體實作與計算實驗 15

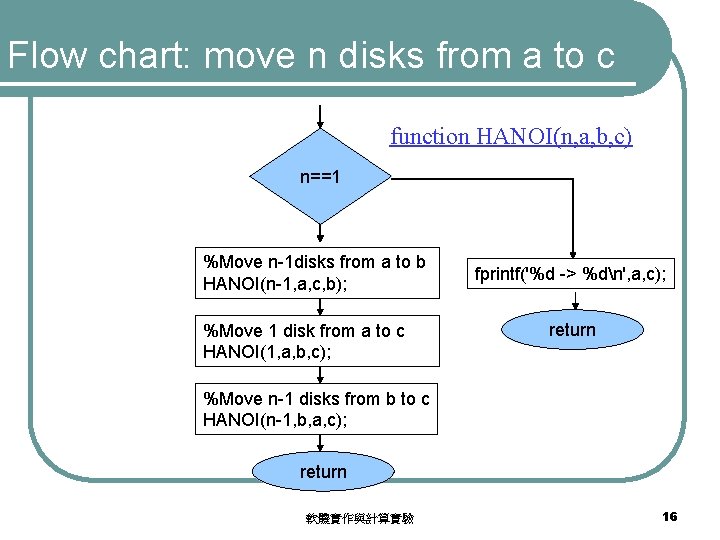
Flow chart: move n disks from a to c function HANOI(n, a, b, c) n==1 %Move n-1 disks from a to b HANOI(n-1, a, c, b); %Move 1 disk from a to c HANOI(1, a, b, c); fprintf('%d -> %dn', a, c); return %Move n-1 disks from b to c HANOI(n-1, b, a, c); return 軟體實作與計算實驗 16

HANOI TOWER HANOI. m 軟體實作與計算實驗 17

Application Evaluation of prefix notations 軟體實作與計算實驗 18

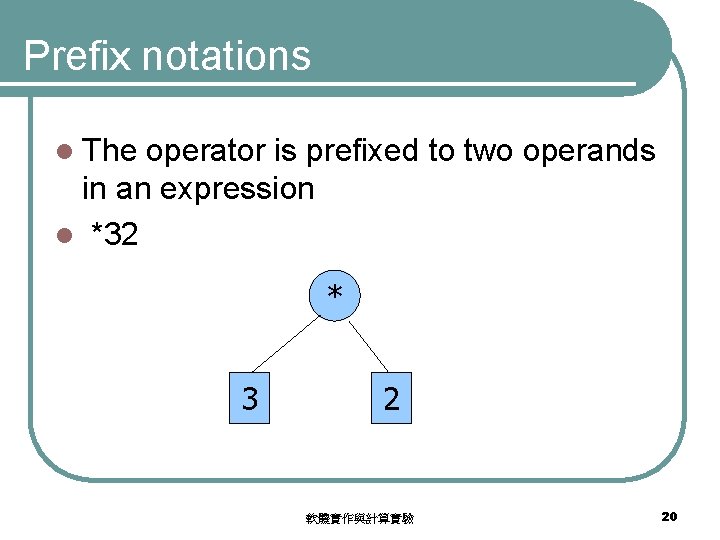
Prefix notations l The operator is prefixed to two operands in an expression l *32 * 3 2 軟體實作與計算實驗 20

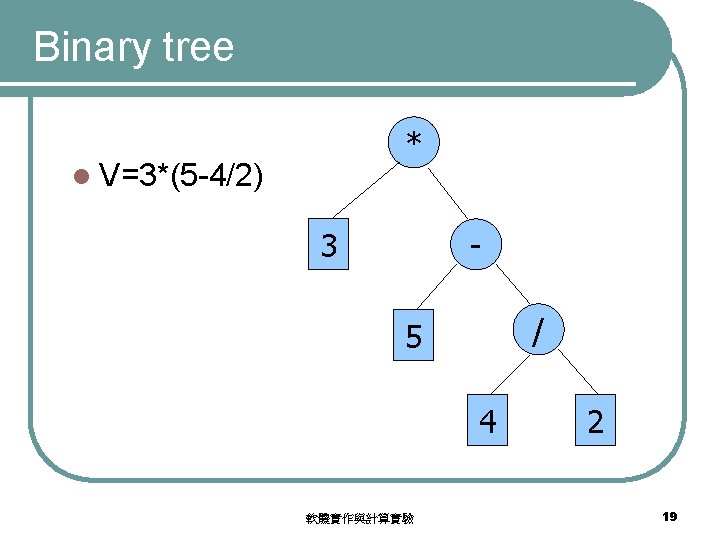
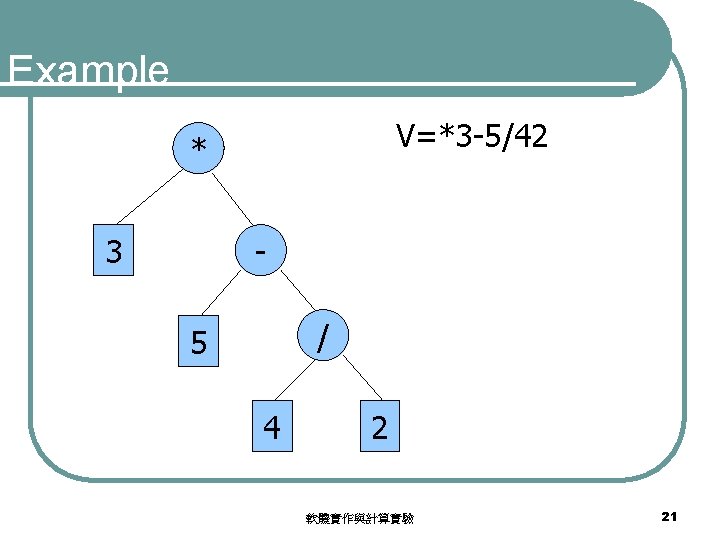
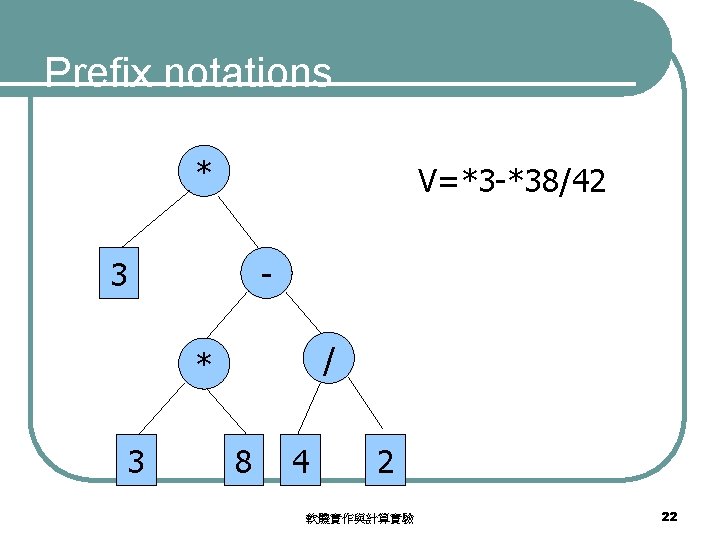
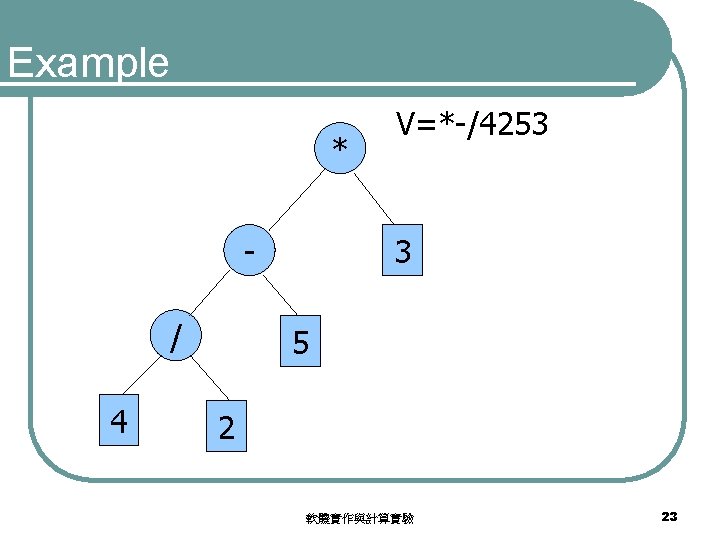
Prefix notations * V=*3 -*38/42 - 3 / * 3 8 4 2 軟體實作與計算實驗 22

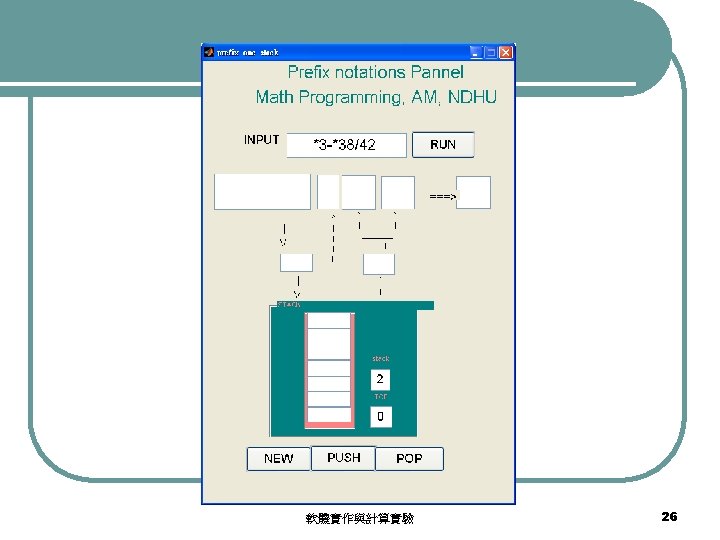
A simulator l Prefix notations simulated here are constrained by Operands in an expression are positive integers within {1, 2, …, 9} l Operators are within {+, -, *, /} l /ab is realized by floor(a/b) l 軟體實作與計算實驗 24

Evaluation of Prefix notations prefix_one_stack. rar 軟體實作與計算實驗 25

n=length(ss) stack= []; top=0; function v = prefix(ss) for i=n: -1: 1 ss(i) –'0' <10 ss(i) –'0' >0 T top=top+1; stack(top)= ss(i)- '0'; top < 2 T v=Na. N; return 軟體實作與計算實驗 c 2= stack(top); c 1=stack(top-1); v=evaluate(ss(i), c 2, c 1); top=top-1; stack(top)= v; 28

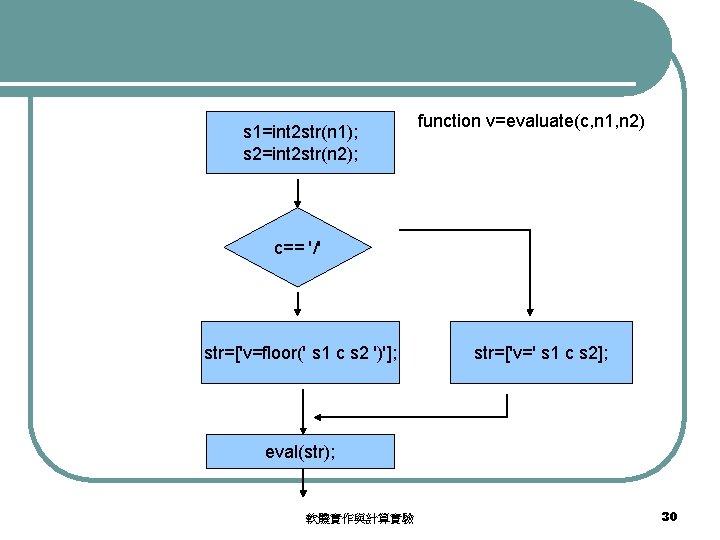
Function evaluate l Apply an operator to two operands. function v=evaluate(c, s 1, s 2) if c=='/' str=['v=floor(' s 1 c s 2 ')']; else str=['v=' s 1 c s 2]; end eval(str); 軟體實作與計算實驗 29

s 1=int 2 str(n 1); s 2=int 2 str(n 2); function v=evaluate(c, n 1, n 2) c== '/' str=['v=floor(' s 1 c s 2 ')']; str=['v=' s 1 c s 2]; eval(str); 軟體實作與計算實驗 30