Lecture 9 Instantaneous velocity If the velocity can

Lecture 9

“Instantaneous” velocity If the velocity can change as time goes on, then we should be able to speak of the velocity at a particular instant of time. The average velocity is measured over a finite time interval ∆t. The instantaneous velocity is in principle the average velocity measured over an infinitesimal time interval dt.

Example An object in free frictionless fall can be modelled by an equation y = 4. 9 t 2, where y=0 is the point where the object was released & down is the +ve y direction. t y dy/dt 0 1 0 4. 9 0 9. 8 2 20 20 3 44 29 4 5 6 7 8 9 10 78 123 176 240 314 397 490 39 49 59 69 78 88 98 600 500 distance 400 300 200 velocity 100 0 1 2 3 4 5 6 7 8 9 10 11 What is the velocity • at time t=4 s? • at time t=8 s? • at time t=12 s? v=dy/dt = 2 x 4. 9 t

Acceleration Rate at which velocity changes with time. Average acceleration: Instantaneous acceleration:

Acceleration e. g. A car can go from rest to 100 km/h in 10 seconds. What is its average acceleration? Use, average acceleration: 100000/60 x 60 =2. 8 m/s 10 e. g. An object has position given by y = 4. 9 t 2. What is its acceleration at t =1? d 2 y/dt 2 = 2 x 4. 9 = 9. 8 m/s 2

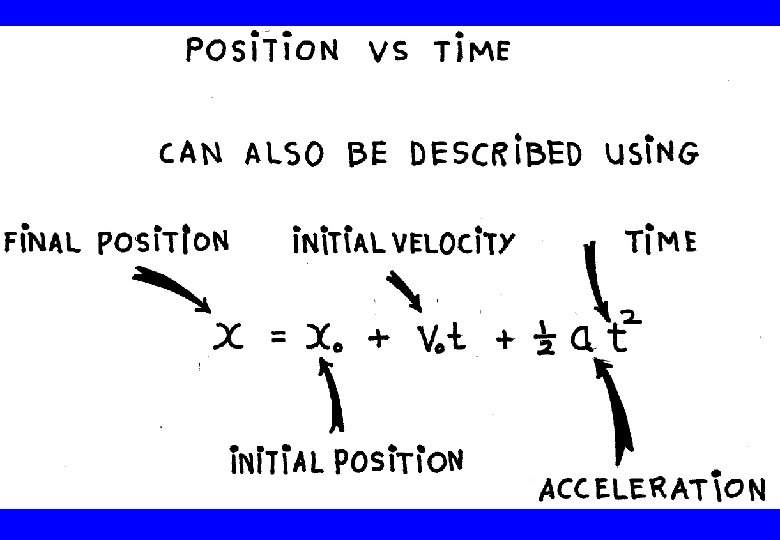
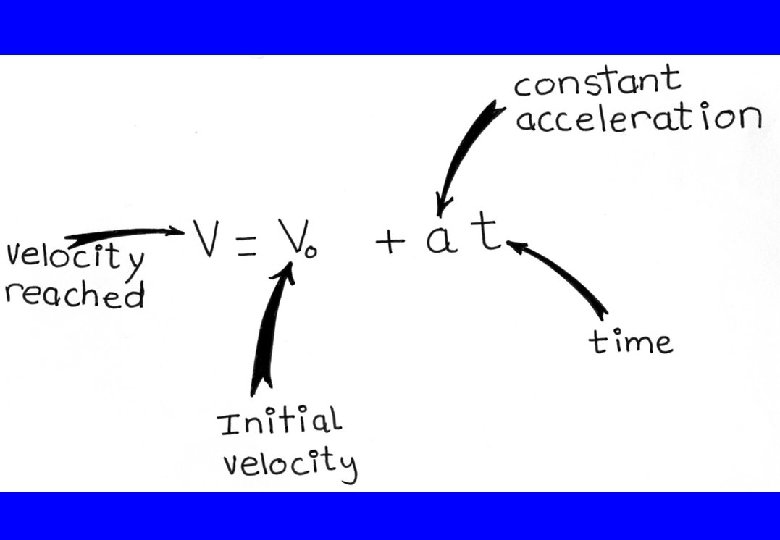
1 -D kinematic models Constant velocity is easy to deal with: x = xi + vt (equivalently ∆x = v∆t) Next step up is dealing with velocity which is changing uniformly, i. e. constant acceleration v=vi + at (or ∆v = a∆t) a= ∆v/ ∆t

Kinematic Model (1 -D, const a) Constant velocity: ∆x = v∆t v Position, ∆x = Area under v vs. t graph Constant ∆t t 0 t acceleration: ∆x = v 0 t + 1/2 at 2 ∆x = Area 1 + Area 2 = v 0 ∆ t + ½ ∆ v ∆t v We know a= ∆ v/ ∆t; so ∆ v=a ∆t So ∆x = v 0 ∆ t + ½ a ∆t ∆t v 0 ∆x = v 0 ∆ t + ½ a ∆t 2 at 2 1 t 0 t

Example An object falls from a height of 100 m and is of a shape where air friction can be ignored. How long does it take to reach the ground? What is its velocity just before impact? ∆y = v 0 t + 1/2 at 2 a = -9. 8 m/s 2 v 0 = 0 ∆y = -100 t = √ 2∆y/a = 4. 5 s v = v 0 + at = 0 - 9. 8 4. 5 = -44 m/s

BUZZ Question A world’s land speed record was set by Colonel John P. Stapp when, on March 19, 1954, he rode a rocket-propelled sled that moved down a track at 1020 km/h. He and the sled were brought to a stop in 1. 4 s. What acceleration did he experience? Express your answer in g units.

Travelling down a track at 1020 km/h. Brought to a stop in 1. 4 s. What acceleration did he experience? Express your answer in g units. Hint: use a=Δv/t=(vf -v 0)/t a=[0 -(1, 020, 000 m/60 x 60 s )]/1. 4 s = -202. 38 m/s 2 in g units, means divide by 9. 8 m/s 2 Answer: about -21 g (decelerating)

Horizontal axis g-force Untrained humans are able to tolerate 17 g “eyeballs-in” (acceleration) and about 12 g “eyeballs-out” (deceleration) for several minutes without loss of consciousness or apparent long-term harm. Stapp survived a peak “eyeballs-out” force of 46. 2 g, and more than 25 g for 1. 1 sec. Stapp lived another 45 years to age 89, but suffered lifelong damage to his vision.

Another example (buzz) An object is projected vertically upwards at a velocity of 20 m/s. (Ignore air friction) How high does it get to? How long before it falls back to ground? What is its velocity just before impact? What is its velocity and acceleration at the topmost point of its trajectory?

Another example An object is projected vertically upwards at a velocity of 20 m/s. (Ignore air friction) How high does it get to? Consider first time to get to top: We have v 0 = 20 m/s and vf = 0 m/s And we know a=-9. 8 m/s 2 Use vf = v 0 + at, solve for t t= 20/9. 8 = 2. 04 s

Another example An object is projected vertically upwards at a velocity of 20 m/s. (Ignore air friction) How high does it get to? We have t= 2. 04 s Use y=y 0 + v 0 t + ½ a t 2 y=0 + 20 x 2. 04 + ½ (-9. 8) (2. 04)2 = 40. 8 -20. 39 =20. 4 m

Another example An object is projected vertically upwards at a velocity of 20 m/s. (Ignore air friction) How long before it falls back to ground? Again use y=y 0 + v 0 t + ½ a t 2 0=20. 4 + 0 + ½ (-9. 8) t 2 t= (2 x 20. 4/9. 8 ) =2. 04 s

Another example An object is projected vertically upwards at a velocity of 20 m/s. (Ignore air friction) What is its velocity just before impact? vf = v 0 + at, = 0 + (-9. 8) 2. 04 = -20 m/s What is its velocity and acceleration at the topmost point of its trajectory? Velocity (top)= 0 m/s Acceleration = -9. 8 m/s 2

Off the Line So far we’ve developed the tools to model motion restricted to a line (“ 1 -dimensional”) -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 The 5 6 7 next step in being able to model realistic motion is to be restricted to a plane (“ 2 -d. . ”) y x

Vectors In 1 -D motion displacement, velocity and acceleration all have one of two directions, represented by their arithmetic sign (+ or -) In 2 -D motion these quantities can have directions ranging over 360°, so simple signs won’t work. They will actually, but we have to get cunning.

Vector Addition Displacements can be added as vectors placed in a “tail-to-head” sequence. y d 1 d 2 d 1 + d 2 The vector sum of a series of displacements is just the resultant displacement. x

Example (buzz) A boat sails a course 3 km due North, then 3 km due East then 5 km 45° East of North. What is the sum of these displacements? y N d 2 d 1 d 3 At the end of the second leg, x = 3000 m, y = 3000 m or d 1 + d 2 + d 3 distance r = √ 1. 8 x 107 m 2 = 4240 m x bearing = 45°

Example A boat sails a course 3 km due North, then 3 km due East then 5 km 45° East of North. What is the sum of these displacements? y N d 2 d 1 d 3 d 1 + d 2 + d 3 x The third leg is a further 5000 m at bearing 45°, so the total displacement is 9240 m at = 45°

Example The third leg in this journey is equivalent to a sequence of two movements, one North (∆y) and the other East (∆x) [order unimportant]. ∆x = d sin ∆y = d cos d ∆x = 5000 sin 45° = 3536 m ∆y = 5000 cos 45° = 3536 m

Recap We’ve done two things: Added vectors to give a resultant Worked out equivalent components of a vector These operations can be represented: graphically, using a scale diagram algebraically, using components (more later) These operations look pretty straightforward for displacement, but apply equally well to velocity and acceleration

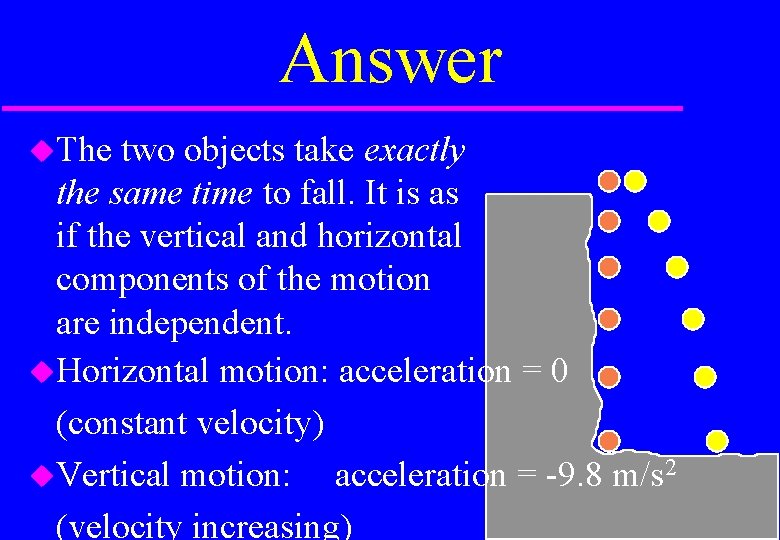
Question If an object was thrown horizontally over a cliff, would you expect it to take longer to hit the ground below than if it was just dropped over?

DEMMO

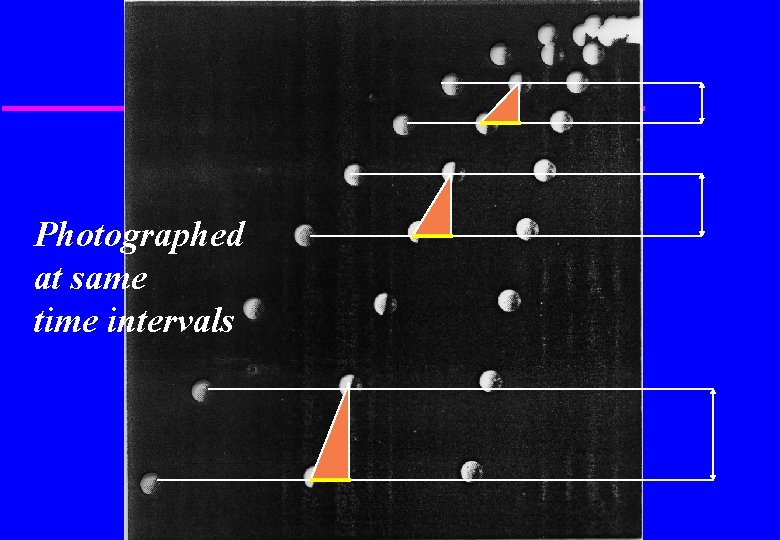
Answer The two objects take exactly the same time to fall. It is as if the vertical and horizontal components of the motion are independent. Horizontal motion: acceleration = 0 (constant velocity) Vertical motion: acceleration = -9. 8 m/s 2 (velocity increasing)

Photographed at same time intervals

Just before impact the yellow ball has a velocity v vx vx is constant throughout vy v ∆x = v 0 x t vy increases with time ∆y = v 0 y t + 1/2 at 2

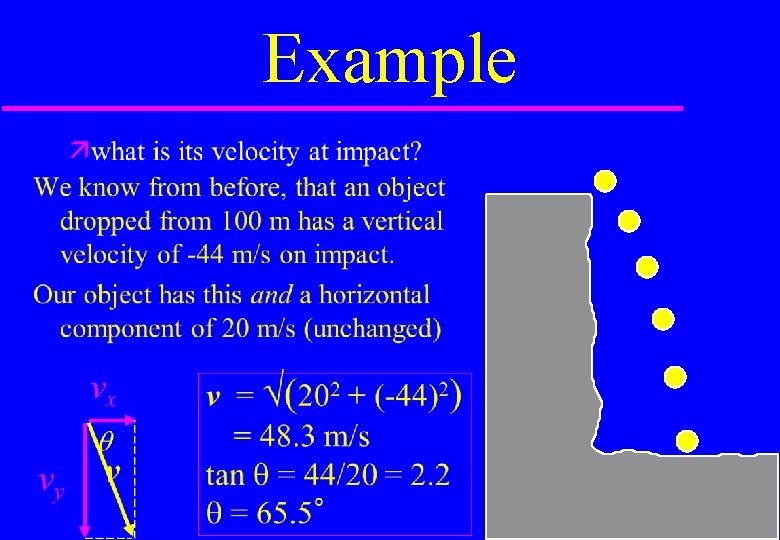
Example (buzz) an object is thrown over a 100 m cliff with an initially horizontal velocity of 20 m/s x If how far out does it land? what is its velocity at impact? y

Example If an object is thrown over a 100 m cliff with an initially horizontal velocity of 20 m/s how far out does it land? what is its velocity at impact? We know from before, that an object dropped from 100 m takes 4. 5 s to land. In this time the horizontal distance travelled is ∆x = v 0 x t =20 m/s x 4. 5 s = 90 m x y

Example