Lecture 9 FIR and IIR Filter design using

Lecture 9 FIR and IIR Filter design using Matlab 2007/11/16 Prof. C. M Kyung

FIR and IIR Filter o GOAL l Linear-Time-Invariant (LTI) system and Impulse response l z-Transform l Characteristics of FIR and IIR filters l Design procedure of FIR and IIR filters

FIR and IIR Filter o LTI System l Input (x(t) or x[n]) and Output (y(t) or y[n]) is defined first n l Linearity n l For a given system, it can be either LTI or non-LTI depending on how we define the input and output. For arbitrary and is the sum the output for , the output of the system for and. (superposition) Time-invariance n Time-shift in input results in time-shift in output by same amount for timeinvariant systems.

FIR and IIR Filter o Impulse Response l Definition n l Impulse response is the output of the system when impulse signal or is applied as the input of the system. Importance n n Impulse response “fully describes” the system if the system is LTI. – Why and how? – Why the impulse response CANNOT fully describe a non-LTI system? Fourier transform of the impulse response shows the characteristic of the system is frequency domain.

FIR and IIR Filter o z-Transform l Definition n l The z-transform of a sequence is defined as Example n For , , l Note n n n z-transform is reduced to discrete-time Fourier transform (DTFT) if is substituted by. This means that z-transform on the unit-circle on the complex plain is same as DTFT. Laplace Transform CTFT ~ z-Transform DTFT

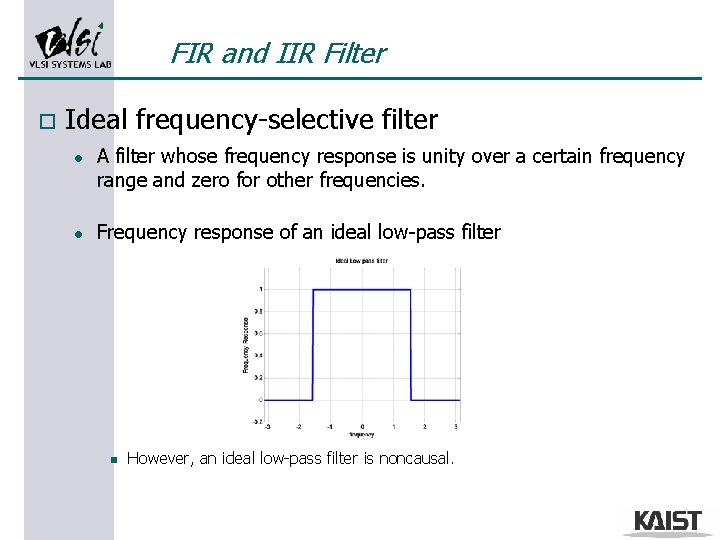
FIR and IIR Filter o Ideal frequency-selective filter l l A filter whose frequency response is unity over a certain frequency range and zero for other frequencies. Frequency response of an ideal low-pass filter n However, an ideal low-pass filter is noncausal.

FIR and IIR Filter o FIR / IIR filter l Definition n l FIR n n l IIR n n If the length of the impulse response is finite, the filter is an FIR (finite impulse response) filter. Otherwise, the filter is an IIR (infinite impulse response) filter. Inherently BIBO (bounded-input, bounded-output) stable Nonzero pole does not exist in its transfer function Easy to implement Can be designed to have linear phase property Sometimes unstable Nonzero pole exists in its transfer function Lower filter order than a corresponding FIR filter Usually have nonlinear phase property

FIR and IIR Filter o Filter Design Procedure l Design continuous-time IIR filter n l Obtain desired using Butterworth, Chebyshev methods Convert it to discrete-time IIR filter using impulse invariance n Impulse invariance : if l , , Obtain discrete-time FIR filter by windowing the IIR filter n n n Windowing : Commonly used windows : rectangular, Bartlett, Hanning, Hamming, Blackman, Kaiser, … However, windowing does not give the optimum solution and other approaches can be used.

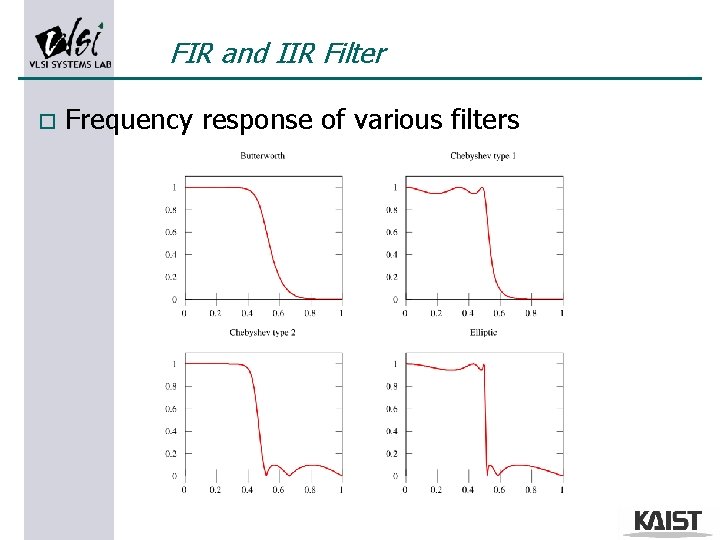
FIR and IIR Filter o Frequency response of various filters

FIR and IIR Filter o Problem Statements l Design several types of FIR and IIR filters n n l Remove the noise in acoustic signal using the filters n l IIR – butterworth, chebyshev type 1, chebyshev type 2, … FIR – using different windows ( Hamming, Hanning, Bartlett, … ) What are the differences between the filters ? Understand the effect of sampling frequency on the sampled signal distortion (aliasing)

FIR and IIR Filter o Experiment Requirements l l PC Matlab software (with signal processing toolbox)

FIR and IIR Filter o References l l l Fundamentals of Signal & System using the web and matlab - Edward W. Kamen, Bonnie S. Heck Discrete-Time Signal Processing - Alan V. Oppenheim, Ronald W. Schafer http: //www. mathworks. com/access/helpdesk/help/toolbox/signal/fi lterde. html