Lecture 9 Divide and Conquer Solving Recurrences Cp

Lecture 9. Divide and Conquer, Solving Recurrences Cp. Sc 212: Algorithms and Data Structures Brian C. Dean School of Computing Clemson University Fall, 2012

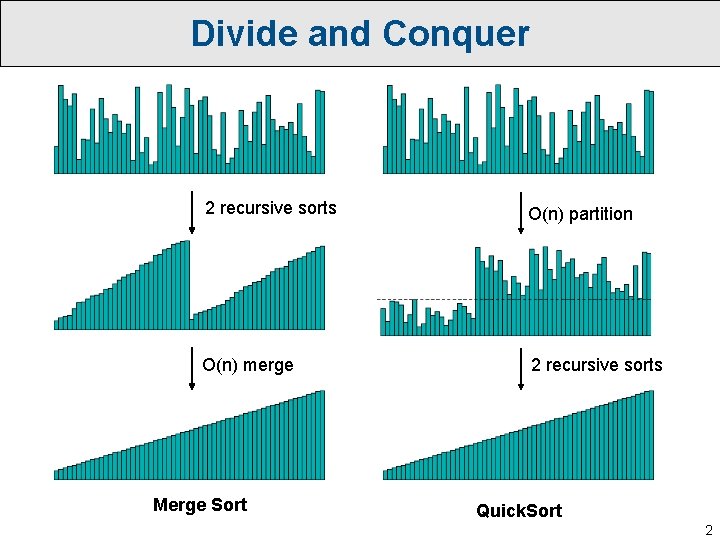
Divide and Conquer 2 recursive sorts O(n) partition O(n) merge 2 recursive sorts Merge Sort Quick. Sort 2

Describing Running Time: Recurrences • To merge sort an array of size n… – We recursively sort two smaller arrays of size n/2. – Then we spend Θ(n) time merging the results. • If T(n) denotes the running time of merge sort on an input of size n, we can therefore write a recurrence (recursive formula) for T(n): T(n) = 2 T(n/2) + Θ(n) As a base case, T(n) = O(1) for n = O(1). • The goal is now to solve the recurrence to produce an explicit (non-recursive) formula for T(n): T(n) = Θ(n log n). 3

Quick Simplifications • Actual merge sort recurrence: • However, since we only care about an asymptotic solution, we can always ignore floors, ceilings, and any other small additive terms (e. g. , T(n/2 + 7) in our recursive calls). • We can also replace the Θ(n) with just n, as this will only change our solution by a constant factor. • So we focus on solving T(n) = 2 T(n/2) + n. 4

Solving by Expansion… • A useful way to solve (or guess the solution to) any recurrence is to simply expand it out a few levels: T(n) = n + 2 T(n/2) = n + 2[n/2 + 2 T(n/4)] = n + 4 T(n/4) = n + 4[n/4 + 2 T(n/8)] = n + n + 8 T(n/8) … = n + n + … + n. T(1) n log n + nΘ(1) = Θ(n log n). 5

Solving Recurrences • Let’s start by considering “divide and conquer” recurrences of the form: T(n) = a. T(n/b) + f(n) with T(n) = O(1) for n = O(1) as a base case. • I. e. , to solve a problem of size n, we recursively solve a subproblems of size n/b, and spend f(n) time during the “division” and “recombination” steps of the algorithm. • The simple form above covers nearly all of the recurrences we’ll encounter in this course… 6

Quick Aside: Asymptotic Behavior of a Geometric Series • Anyone remember how to sum a geometric series? S = n 2 + (3/4)2 n 2 + … + (3/4)k n 2 = n 2 [1 + (3/4)2 + … + (3/4)k] ≤ n 2 [1 + (3/4)2 + …] 7

Quick Aside: Asymptotic Behavior of a Geometric Series • Anyone remember how to sum a geometric series? S = n 2 + (3/4)2 n 2 + … + (3/4)k n 2 = n 2 [1 + (3/4)2 + … + (3/4)k] ≤ n 2 [1 + (3/4)2 + …] = 4 n 2. • A decreasing geometric series behaves asymptotically just like its 1 st term: S = Θ(n 2). • By symmetry, if S were increasing, it would behave asymptotically like its final term: T = n 2 + 2 n 2 + … + 2 kn 2 = Θ(2 kn 2). 8

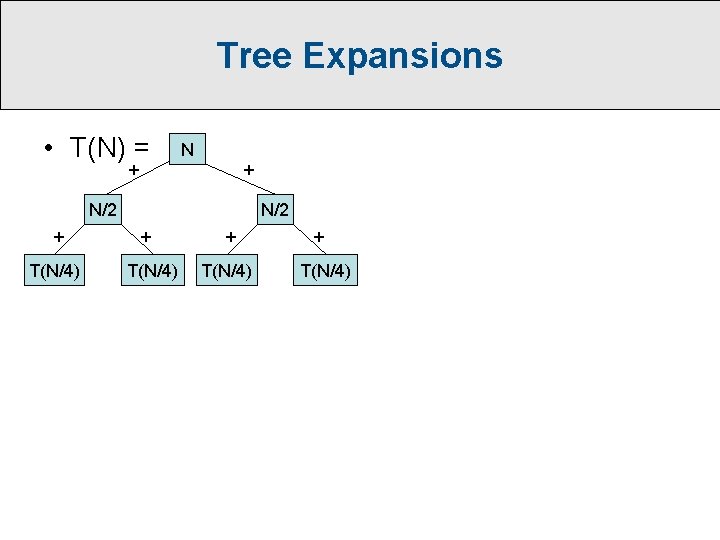
Tree Expansions • T(N) = N + 2 T(N/2)

Tree Expansions • T(N) = + T(N/2) N + T(N/2)

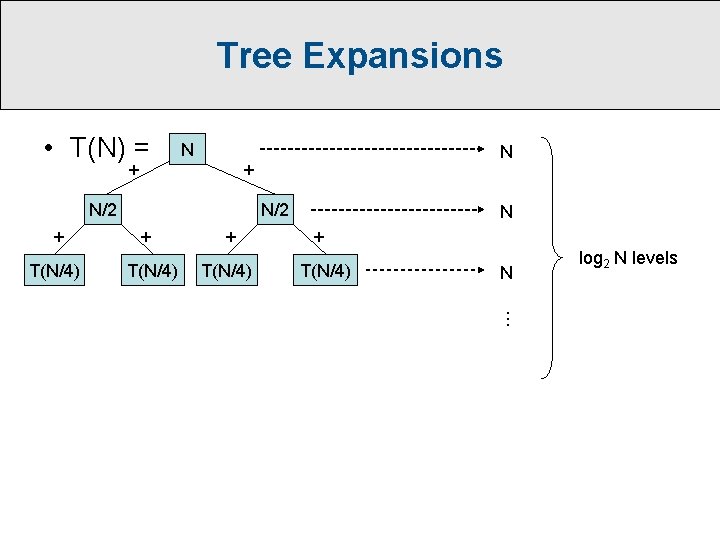
Tree Expansions • T(N) = N + + N/2 + T(N/4)

Tree Expansions • T(N) = N + + N/2 + T(N/4) N + T(N/4) N log 2 N levels …

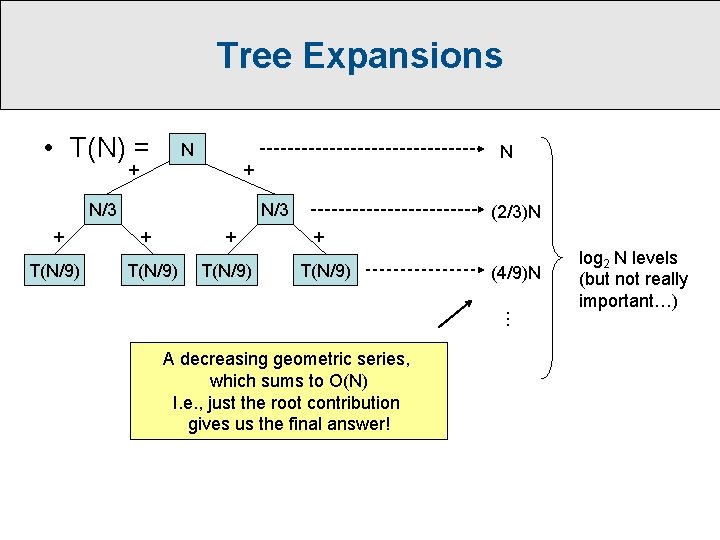
What about… • T(N) = N + 2 T(N/3)

Tree Expansions • T(N) = N + + N/3 + T(N/9) N N/3 + + T(N/9) (2/3)N + T(N/9) (4/9)N … A decreasing geometric series, which sums to O(N) I. e. , just the root contribution gives us the final answer! log 2 N levels (but not really important…)

Quick Practice • T(N) = N + 17 T(N / 17) • T(N) = N + 16 T(N / 17)

Quick Practice • T(N) = N + 17 T(N / 17) • T(N) = N + 16. 99999 T(N / 17)

Quick Practice • • T(N) = N + 17 T(N / 17) T(N) = N + 16. 99999 T(N / 17) T(N) = N + 18 T(N / 17) (!? !? !)

The “Master Method” • Consider T(n) = a. T(n/b) + nα. • There are logb n levels in the tree, and our branching factor is a, so the total # of leaves is alogb n = nlogb a. • Since each leaf contributes Θ(1), the total leaf contribution is Θ(np), where p = logb a. • We can now say that T(n) = Θ(nα) Θ(nα log n) Θ(np) if α > p if α = p if α < p (decreasing series) (unchanging series) (increasing series) • This formula is sometimes called the master method for solving a divide-and conquer recurrence. (don’t forget the tree expansion intuition though!) 18

Practice • Let’s solve the following recurrences: T(n) = 2 T(n/2) + Θ(n) T(n) = Θ(n log n) T(n) = 3 T(n/2) + Θ(n) T(n) = Θ(nlog(2) 3) T(n) = 3 T(n/2) + Θ(n 2) T(n) = 4 T(n/2) + Θ(n 2) T(n) = Θ(n 2 log n) T(n) = 8 T(n/3) + Θ(n 2) T(n) = 81 T(n/3) + Θ(n 4) T(n) = Θ(n 4 log n) T(n) = 1023 T(n/2) + Θ(n 10) T(n) = T(n/2 - 6) + T(n/2 + 10) + Θ(n) T(n) = T(n/2) + T(n/3) + T(n/6) + Θ(n) T(n) = 2 T(n/2) + Θ(n log n) 19

Maximum Subarray • Given an array A[1…n] of numbers, find a subarray A[i…j] whose elements have maximum sum. 20

Maximum Subarray • Given an array A[1…n] of numbers, find a subarray A[i…j] whose elements have maximum sum. • Trivial approach: spend O(n) time checking all (n 2) subarrays, for a total of O(n 3). • Slightly faster: use prefix sums to check each subarray in O(1) time, for a total of O(n 2). • Better yet: Use divide and conquer -- O(n log n). • Best: Dynamic programming gives an even simpler O(n) algorithm, which we’ll discuss later in the semester. 21

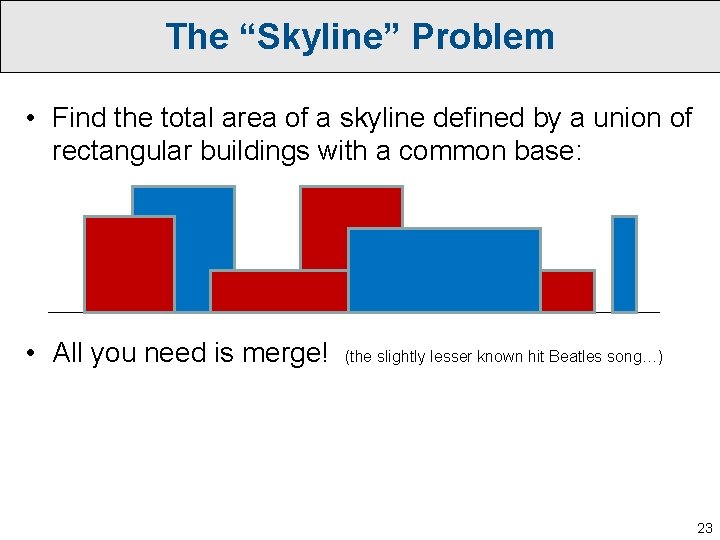
The “Skyline” Problem • Find the total area of a skyline defined by a union of rectangular buildings with a common base: 22

The “Skyline” Problem • Find the total area of a skyline defined by a union of rectangular buildings with a common base: • All you need is merge! (the slightly lesser known hit Beatles song…) 23

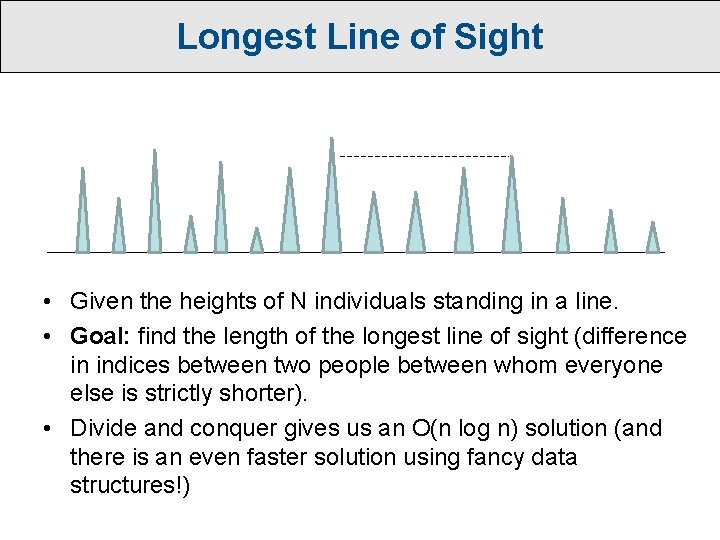
Longest Line of Sight • Given the heights of N individuals standing in a line. • Goal: find the length of the longest line of sight (difference in indices between two people between whom everyone else is strictly shorter). • Divide and conquer gives us an O(n log n) solution (and there is an even faster solution using fancy data structures!)

In-Place Perfect Shuffle • Start with two length-n arrays stored consecutively in 2 n memory locations like this: A[1] A[2] A[3] … A[n] B[1] B[2] B[3] … B[n] • We would like to rearrange it so it’s stored as: A[1] B[1] A[2] B[2] A[3] B[3] … A[n] B[n] • However, we want to rearrangement to happen “in place”, without allocating extra scratch space. 25

In-Place Perfect Shuffle A[1] A[2] … A[n/2] A[n/2+1] … A[n] B[1] B[2] … B[n/2] B[n/2+1] … B[n] O(n) A[1] A[2] … A[n/2] B[1] B[2] … B[n/2] T(n/2) A[1] B[1] A[2] B[2] … A[n/2] B[n/2] A[n/2+1] … A[n] B[n/2+1] … B[n] T(n/2) A[n/2+1] B[n/2+1] … A[n] B[n] 26

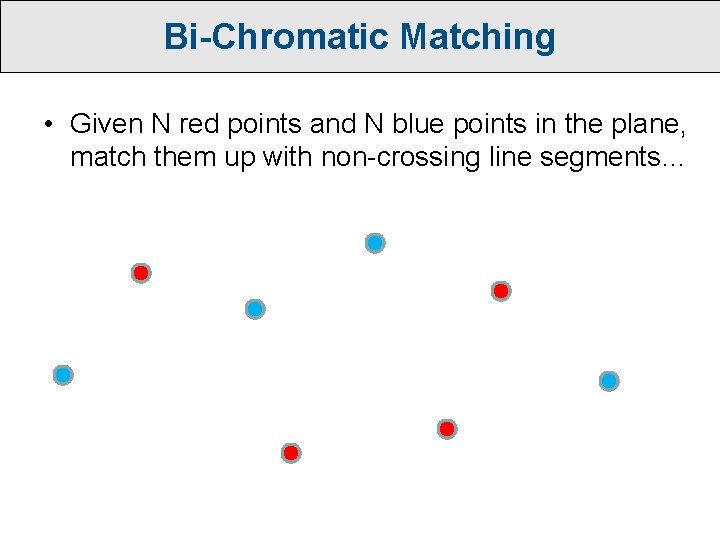
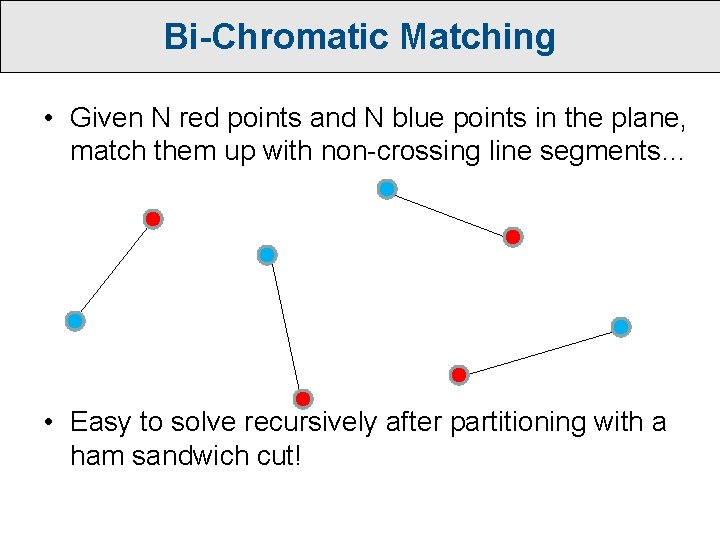
Bi-Chromatic Matching • Given N red points and N blue points in the plane, match them up with non-crossing line segments…

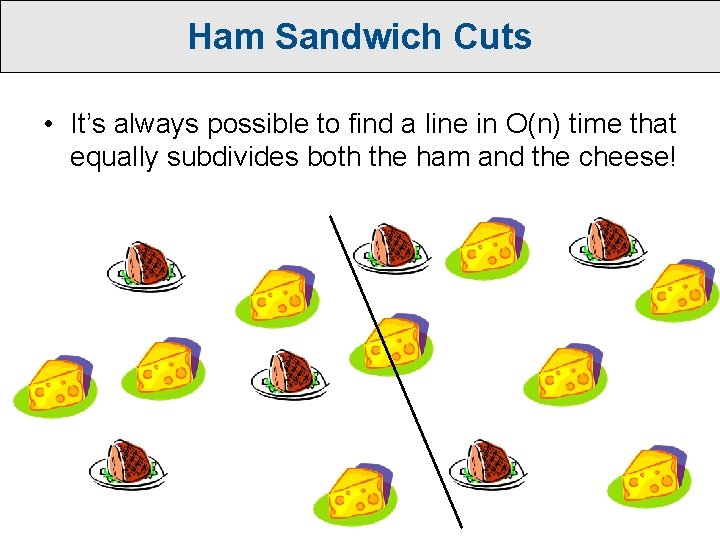
Ham Sandwich Cuts • It’s always possible to find a line in O(n) time that equally subdivides both the ham and the cheese!

Bi-Chromatic Matching • Given N red points and N blue points in the plane, match them up with non-crossing line segments… • Easy to solve recursively after partitioning with a ham sandwich cut!

Finding a Local Maximum • You are given the ability to evaluate some function F(x, y), defined for integer values of x and y in the range 1…n. • You are also told F(x, y) is different for every possible (x, y). • Goal: Find a point (x, y) that is a local max of F; that is, a point (x, y) for which F(x, y) is larger than F(x-1, y), F(x+1, y), F(x, y-1) and F(x, y+1). • Your algorithm should run in closer to O(n) time than O(n 2) time. 30

Linked List Ending in a Loop • You are given a pointer to the beginning of a linked list. • It either ends by pointing to NULL: NULL or it ends by pointing back into itself, forming a loop: • Goal: Determine as quickly as possible which of these two cases is occurring. • To make things interesting: You aren’t allowed to modify the list, or to use substantial amounts of extra memory…

The Firing Squad Problem • N parallel processors hooked together in a line: • Each processor doesn’t know N, and only has a constant number of bits of memory (so it can’t even count to N). • Processors synchronized to a global clock. In each time step, a processor can: – Perform some simple calculation. – Exchange messages with its neighbors. • At some point in time, we give the leftmost processor a “ready!” message. • Sometime in the future, we want all the processors to enter the same state “fire!” all in the same time step.

The Firing Squad Problem • N parallel processors hooked together in a line: • Each processor doesn’t know N, and only has a constant number of bits of memory (so it can’t even count to N). • Processors synchronized to a global clock. In each time step, a processor can: – Perform some simple calculation. – Exchange messages with its neighbors. • At some point in time, we give the leftmost processor a “ready!” message. • Sometime in the future, we want all the processors to enter the same state “fire!” all in the same time step.

Final Awesome Application: Detecting Infinite Loops • Can we tell if a program (running, say, in a virtual machine under our control) has entered an infinite loop? – I. e. , has the program reached a state where its memory contents is identical to that of some previous state? 34

Final Awesome Application: Detecting Infinite Loops • Can we tell if a program (running, say, in a virtual machine under our control) has entered an infinite loop? – I. e. , has the program reached a state where its memory contents is identical to that of some previous state? • Yes! Run two instances of the program, one twice as fast as the other, and use hashing to detect if they ever reach the same state. – Use a polynomial hash function to hash the entire memory contents; recall this can be updated quickly if just one memory cell changes. 35