Lecture 9 Control Engineering REVIEW SLIDES Reference Textbook

Lecture #9 Control Engineering REVIEW SLIDES Reference: Textbook by Phillips and Habor

Mathematical Modeling

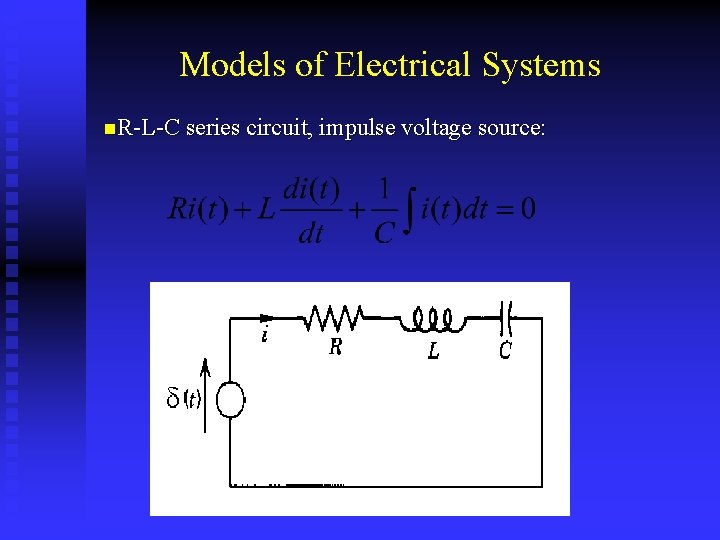
Models of Electrical Systems n. R-L-C series circuit, impulse voltage source:

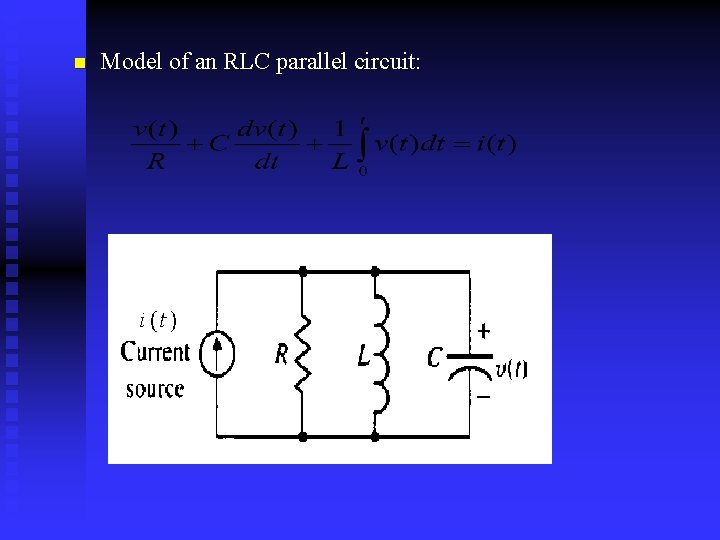
n Model of an RLC parallel circuit:

n Kirchhoff’ s voltage law: The algebraic sum of voltages around any closed loop in an electrical circuit is zero. n Kirchhoff’ s current law: The algebraic sum of currents into any junction in an electrical circuit is zero.

Models of Mechanical Systems Mechanical translational systems. n Newton’s second law: n Device with friction (shock absorber): n B is damping coefficient. Translational system to be defined is a spring (Hooke’s law): K is spring coefficient

n Model of a mass-spring-damper system: n Note that linear physical systems are modeled by linear differential equations for which linear components can be added together. See example of a mass-spring-damper system.

n Simplified automobile suspension system:

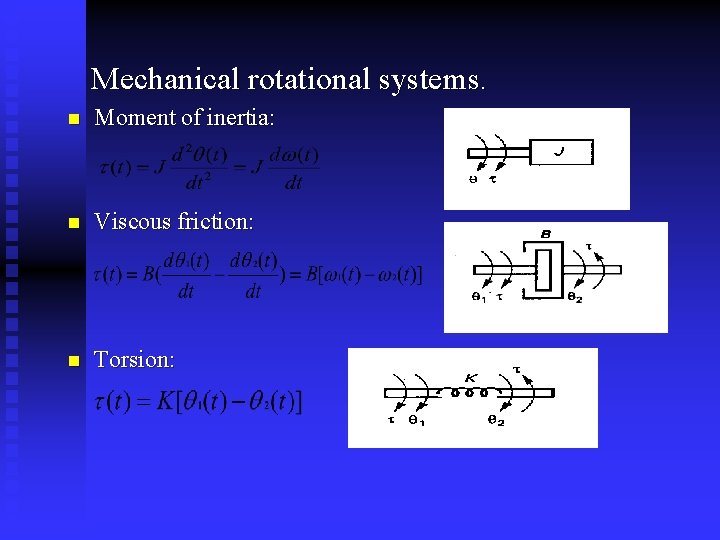
Mechanical rotational systems. n Moment of inertia: n Viscous friction: n Torsion:

n Model of a torsional pendulum (pendulum in clocks inside glass dome); Moment of inertia of pendulum bob denoted by J Friction between the bob and air by B Elastance of the brass suspension strip by K

n Differential equations as mathematical models of physical systems: similarity between mathematical models of electrical circuits and models of simple mechanical systems (see model of an RCL circuit and model of the mass-spring-damper system).

Laplace Transform

Name Unit Impulse Unit Step Unit ramp nth-Order ramp Exponential Time function f(t) u(t) t tn e-at nth-Order exponential t n e-at Sine sin(bt) Cosine cos(bt) Damped sine e-at sin(bt) Damped cosine e-at cos(bt) Diverging sine t sin(bt) Diverging cosine t cos(bt) Laplace Transform 1 1/s 2 n!/sn+1 1/(s+a) n!/(s+a)n+1 b/(s 2+b 2) s/(s 2+b 2) b/((s+a)2+b 2) (s+a)/((s+a)2+b 2) 2 bs/(s 2+b 2)2 (s 2 -b 2) /(s 2+b 2)2

Find the inverse Laplace transform of F(s)=5/(s 2+3 s+2). Solution:

Find inverse Laplace Transform of

Find the inverse Laplace transform of F(s)=(2 s+3)/(s 3+2 s 2+s). n Solution:

Laplace Transform Theorems

Transfer Function

Transfer Function n After Laplace transform we have X(s)=G(s)F(s) n We call G(s) the transfer function.

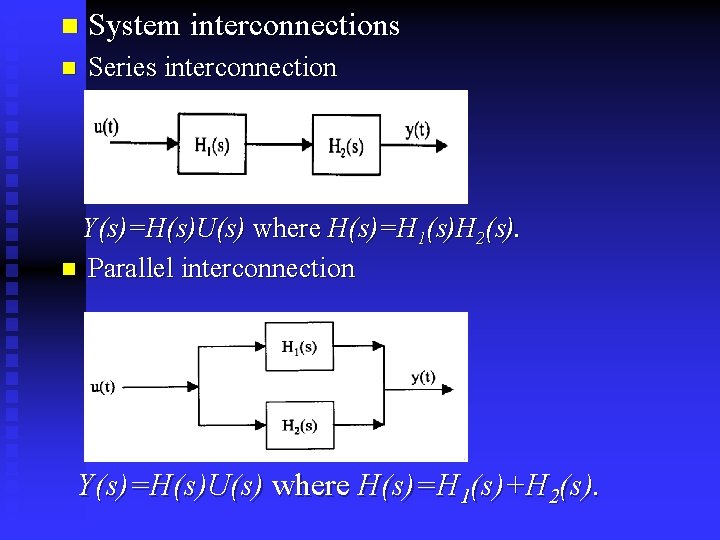
n System interconnections n Series interconnection Y(s)=H(s)U(s) where H(s)=H 1(s)H 2(s). n Parallel interconnection Y(s)=H(s)U(s) where H(s)=H 1(s)+H 2(s).

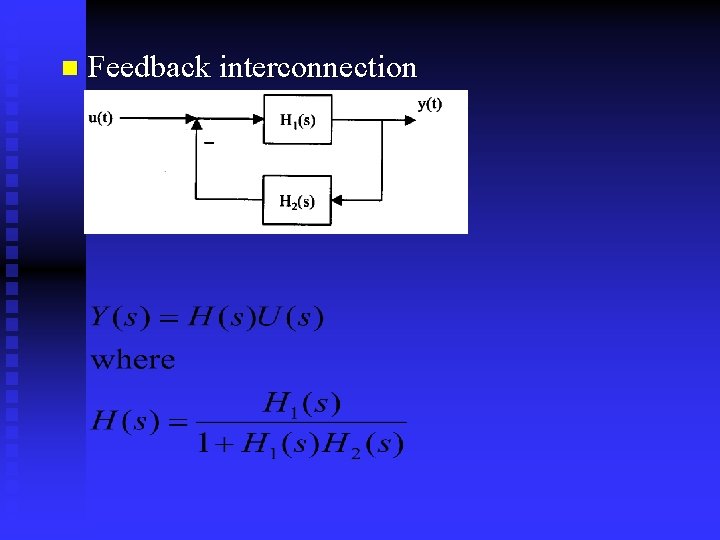
n Feedback interconnection

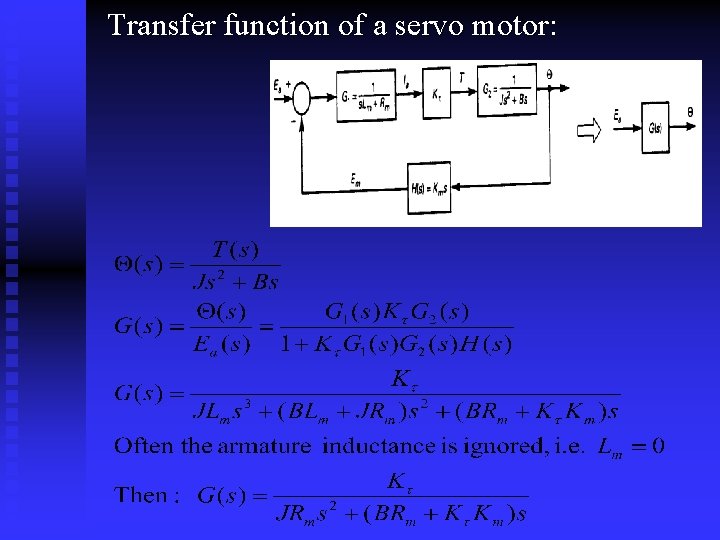
Transfer function of a servo motor:

Mason’s Gain Formula This gives a procedure that allows us to find the transfer function, by inspection of either a block diagram or a signal flow graph. n Source Node: signals flow away from the node. n Sink node: signals flow only toward the node. n Path: continuous connection of branches from one node to another with all arrows in the same direction. n

Loop: a closed path in which no node is encountered more than once. Source node cannot be part of a loop. n Path gain: product of the transfer functions of all branches that form the loop. n Loop gain: products of the transfer functions of all branches that form the loop. n Nontouching: two loops are non-touching if these loops have no nodes in common. n

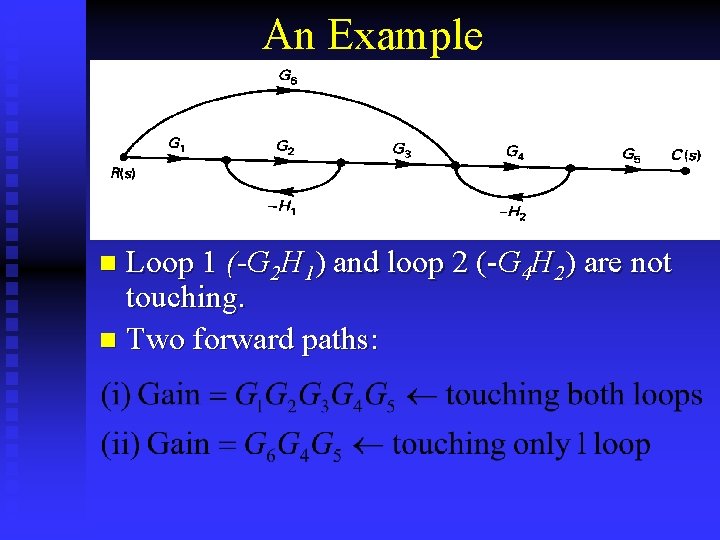
An Example Loop 1 (-G 2 H 1) and loop 2 (-G 4 H 2) are not touching. n Two forward paths: n

State Variable System:

n Solutions of state equations:

Responses

System Responses (Time Domain) n First order systems: Transient response Steady state response Step response Ramp response Impulse response n Second order systems Transient response Steady state response Step response Ramp response Impulse response

Time Responses of first order systems The T. F. for first order system:

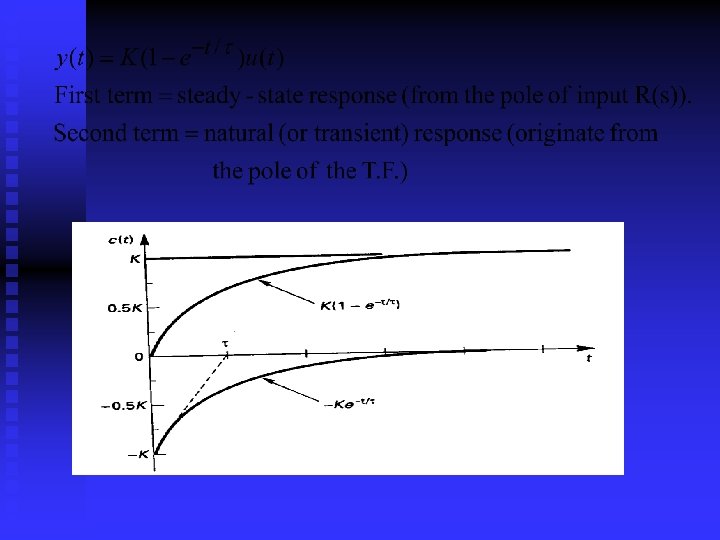
n n is called the time constant Ex. Position control of the pen of a plotter for a digital computer: is too slow, is faster.

System DC Gain n In general: