Lecture 9 Balanced Search Trees BongSoo Sohn Assistant

Lecture 9 : Balanced Search Trees Bong-Soo Sohn Assistant Professor School of Computer Science and Engineering Chung-Ang University

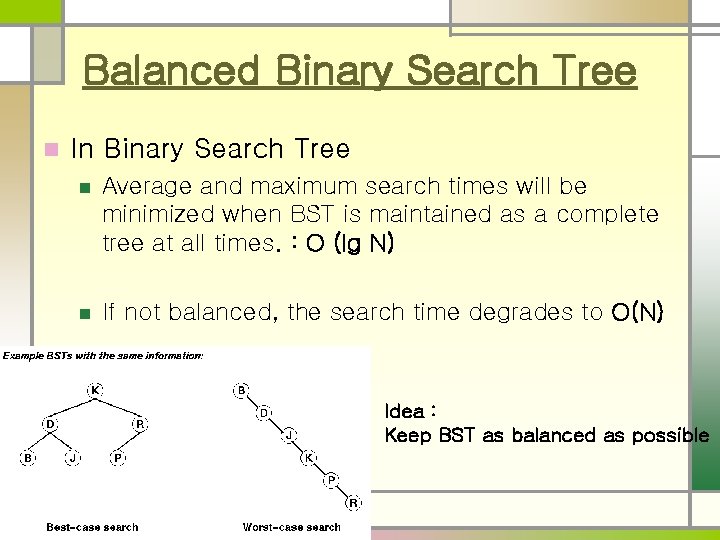
Balanced Binary Search Tree n In Binary Search Tree n Average and maximum search times will be minimized when BST is maintained as a complete tree at all times. : O (lg N) n If not balanced, the search time degrades to O(N) Idea : Keep BST as balanced as possible

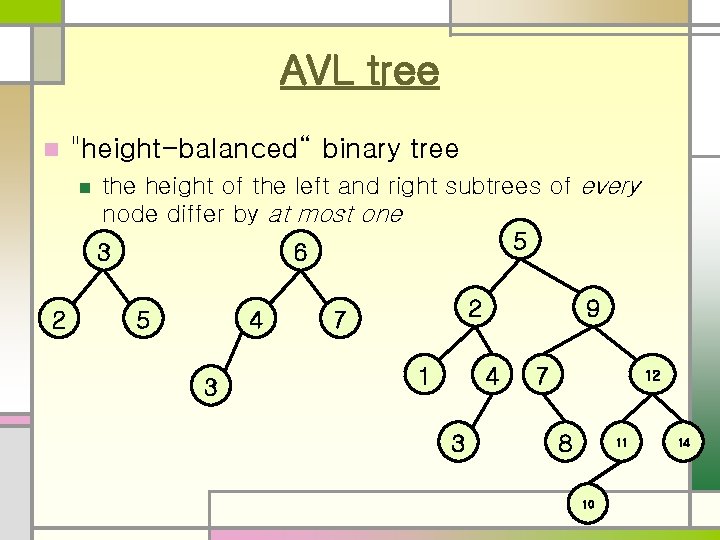
AVL tree n "height-balanced“ binary tree n 2 the height of the left and right subtrees of every node differ by at most one 5 3 6 5 4 3 2 7 1 9 4 3 7 12 8 11 10 14

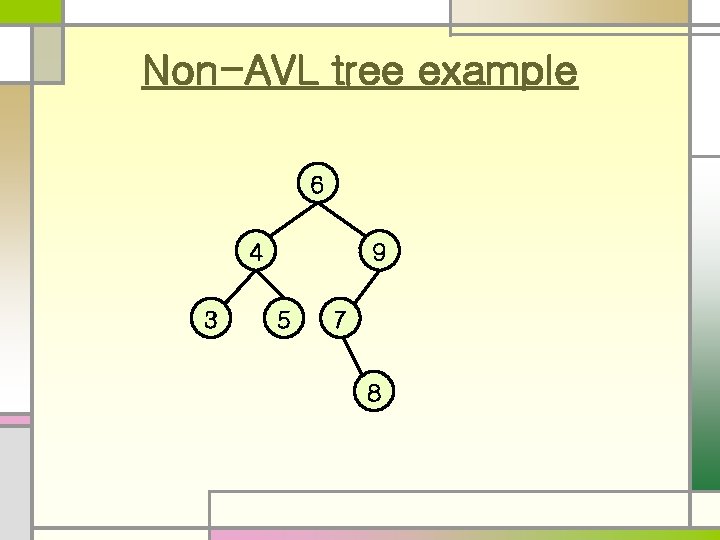
Non-AVL tree example 6 4 3 9 5 7 8

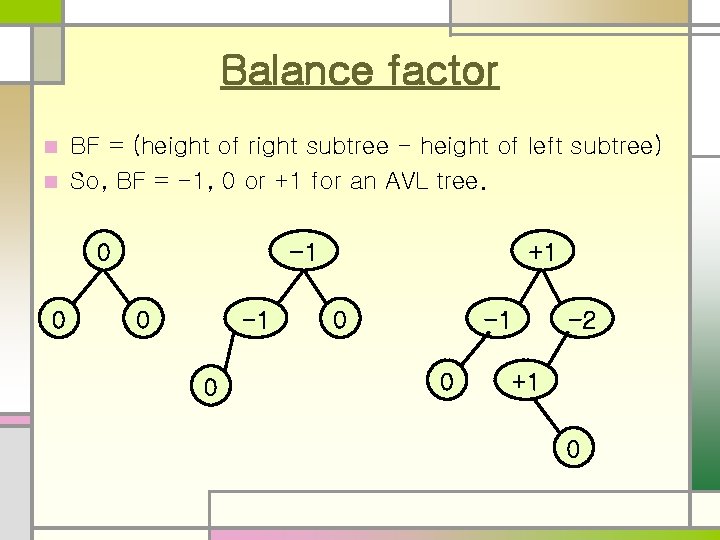
Balance factor BF = (height of right subtree - height of left subtree) n So, BF = -1, 0 or +1 for an AVL tree. n 0 0 -1 0 +1 0 -2 +1 0

AVL tree rebalancing n When the AVL property is lost we can rebalance the tree via one of four rotations n n Single right rotation Single left rotation Double right rotation

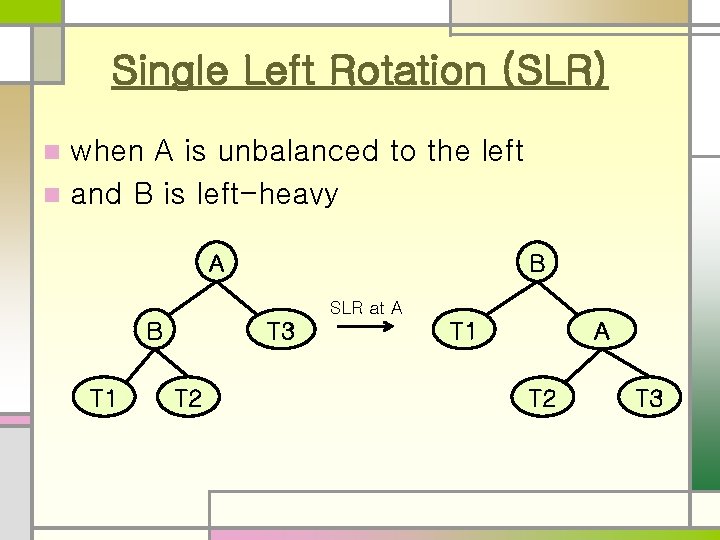
Single Left Rotation (SLR) when A is unbalanced to the left n and B is left-heavy n A B SLR at A B T 1 T 3 T 2 T 1 A T 2 T 3

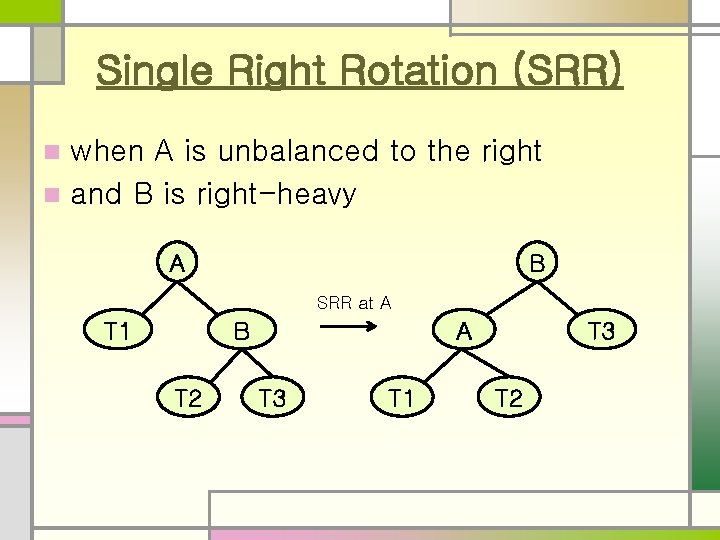
Single Right Rotation (SRR) when A is unbalanced to the right n and B is right-heavy n A B SRR at A T 1 B T 2 A T 3 T 1 T 3 T 2

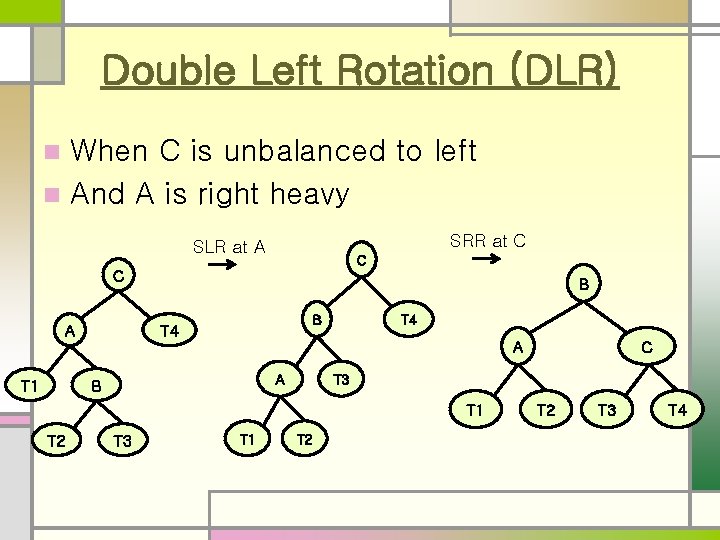
Double Left Rotation (DLR) When C is unbalanced to left n And A is right heavy n SRR at C SLR at A C C A B B T 4 A T 1 A B T 3 T 1 T 2 T 3 T 1 C T 2 T 3 T 4

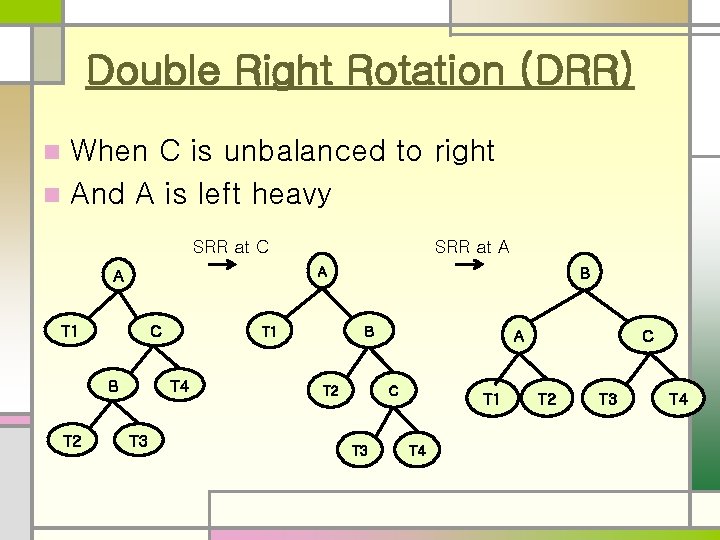
Double Right Rotation (DRR) When C is unbalanced to right n And A is left heavy n SRR at C A A T 1 C B T 2 SRR at A T 1 T 4 T 3 B B T 2 A C T 3 T 1 T 4 C T 2 T 3 T 4

Insertion in AVL tree n An AVL tree may become out of balance in two basic situations n n After inserting a node in the right subtree of the right child After inserting a node in the left subtree of the right child

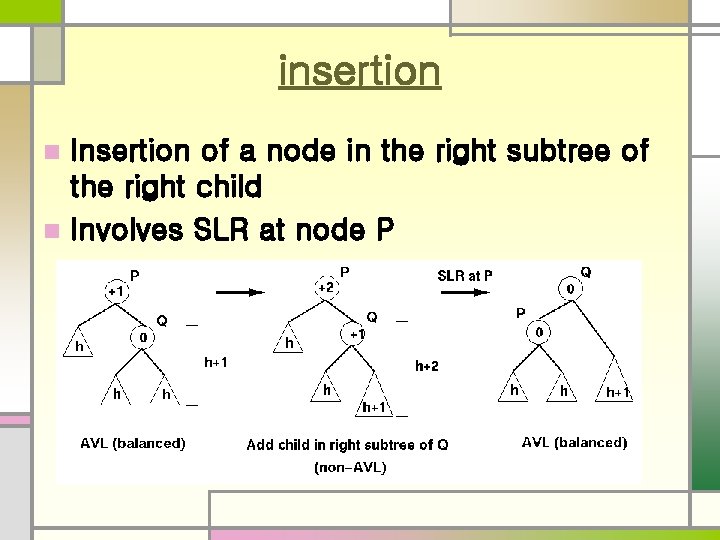
insertion Insertion of a node in the right subtree of the right child n Involves SLR at node P n

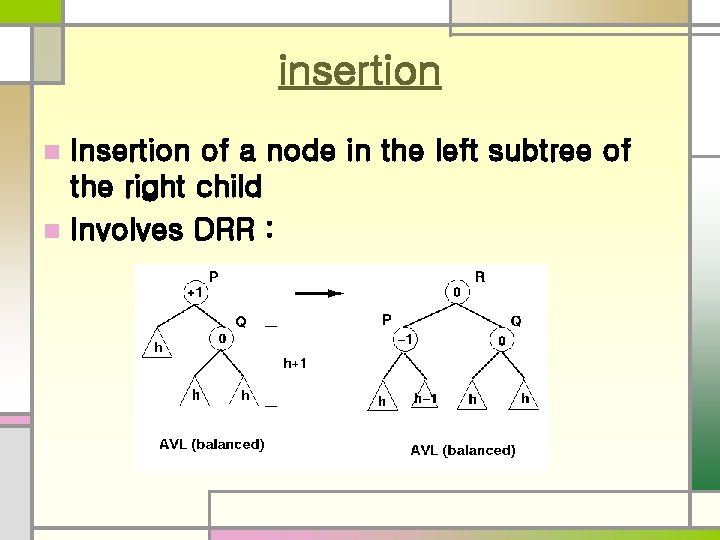
insertion Insertion of a node in the left subtree of the right child n Involves DRR : n

insertion In each case the tree is rebalanced locally n insertion requires one single or one double rotation n O(constant) for rebalancing n Cost of search for insert is still O(lg N) n n Experiments have shown that 53% of insertions do not bring the tree out of balance

Deletion in AVL tree Not covered here n Requires O(lg N) rotations in worst case n

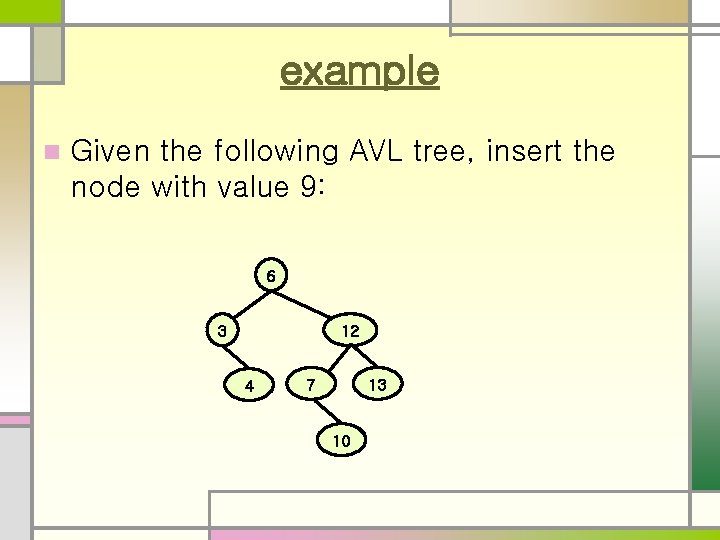
example n Given the following AVL tree, insert the node with value 9: 6 3 12 4 7 13 10