Lecture 9 2 Equilibrium Concentrations and Reaction Quotient

Lecture 9. 2 Equilibrium Concentrations and Reaction Quotient

I. ICE Tables Equilibrium Positions: Set of equilibrium []s Equilibrium [ ] depend on initial [ ]. Equil. constants (at a given temp. ) will stay the same.

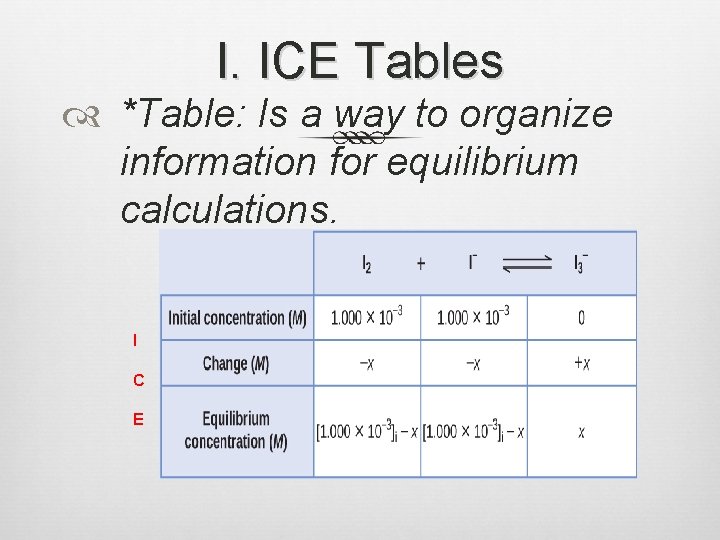
I. ICE Tables *Table: Is a way to organize information for equilibrium calculations. I C E

I. ICE Tables Ex #1: Initially, [CO] = 0. 27 M and [H 2] = 0. 49 M. At equilibrium, [CH 3 OH] is 0. 11 M. Find K at this temperature. CO(g) + 2 H 2(g) CH 3 OH(g)

Answer Ex #1 CO(g) + 2 H 2(g) CH 3 OH(g) 0. 27 M -x 0. 27 -x 0. 49 M -2 x +x 0. 49 -2 x 0. 11 K = [CH 3 OH]/[CO][H 2]2 = [0. 11]/[0. 16][0. 27]2 = 9. 4 +x 0. 27 –x= 0. 11 x= 0. 16

Ice Tables Ex: #2 Consider the following Reaction: CO(g) + 2 H 2(g) <--> CH 3 OH(g) A reaction mixture at 7800 C initially contains [CO]=0. 500 M and [H 2]=1. 00 M. At equilibrium, the CO concentration is found to be 0. 15 M. What is the value of the equilibrium constant, K?

Answer Ex: #2 CO(g) + 2 H 2(g) <--> CH 3 OH(g) I 0. 500 M C (-x) E 0. 15 1. 00 M (-2 x) (1. 00 -2 x) Find x: Therefore, 0. 500 - x = 0. 15 => x = 0. 35 (+x) x

Ex#2 Continued CO(g) + 2 H 2(g) I 0. 500 M C (-0. 35) E 0. 15 <--> CH 3 OH(g) 1. 00 M (-0. 70) (0. 35) 0. 30 0. 35 K = [CH 3 OH]/[CO][H 2]2 = (0. 35)/(0. 15) x (0. 30) 2 = 25. 9

II. Reaction Quotient The reaction quotient (Q) is based on [ ] at any point in the rxn, not just at equil.

II. Reaction Quotient If rxn contains only reactants, Q =0. If rxn contains only products, Q =∞. If rxn contains equal amounts of reactants and products, Q =1.

II. Reaction Quotient If: Q < K, rxn proceeds to the right. Q > K, rxn proceeds to the left. Q = K, rxn is at equil.

II. Reaction Quotient Ex #3: A reaction mixture contains [NO 2] = 0. 0255 M and [N 2 O 4] = 0. 0331 M. Find Q and determine in which direction the reaction will proceed. N 2 O 4(g) 2 NO 2(g) K = 5. 85 × 10 -3

III. Equilibrium Concentrations Given: K and initial [ ]. Unknown: equil. [ ]. Plan: Use an ICE table and algebra.

III. Equilibrium Concentrations Ex #4: Initially, [N 2 O 4] = 0. 0243 M and there is no product. Find the equilibrium concentrations of each when K = 0. 36 N 2 O 4(g) 2 NO 2(g)

Answer Ex #4: I N 2 O 4(g) 2 NO 2(g) 0. 0199=0. 004 0. 0243 M C (-x) E 0. 0243 -x +2 x [NO 2 O 4]= 0. 0243[NO 2]= 2(0. 0199)=0. 0398 (+2 x) 2 x K= [NO 2]2/[NO 2 O 4]= 2 x 2/0. 0243 -x=0. 36 4 x 2=(0. 36)(0. 0243 -x) 4 x 2=0. 008748 -0. 36 x

III. Equilibrium Concentrations When K is small, x (the equilibrium product concentration) is also small. Use the x is small approximation.

III. Equilibrium Concentrations Ex #5: Initially, [H 2 S] = 1. 00 × 10 -4 M and there are no products. Find the equilibrium concentrations when K =1. 67 × 10 -7. 2 H 2 S(g) 2 H 2(g) + S 2(g)

PS 9. 2 Read section 13. 5 -13. 6 Ch. 13: #33, 37, 39, 43, 55