Lecture 9 0 Silicon OxidationDiffusionImplantation Silicon Oxidation l





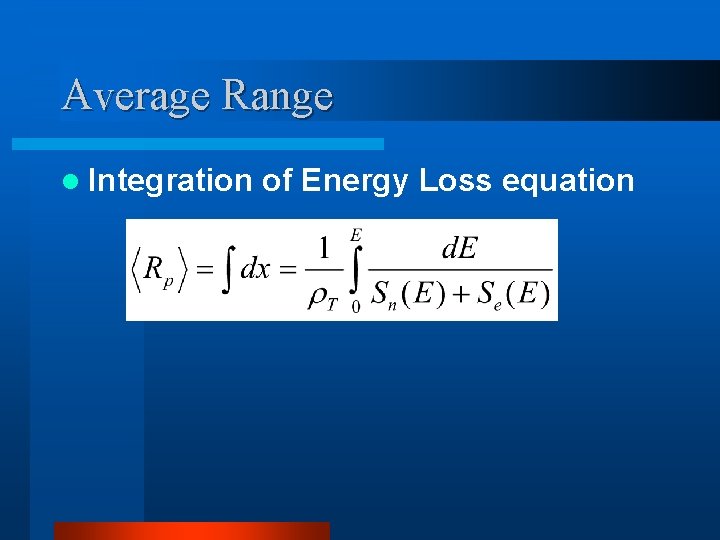



![Implantation Concentration Profile Probability Based l N(x)=Nmax exp[(x-xave)2/2 x 2] l Nmax=(Ndose/[ (2 ) Implantation Concentration Profile Probability Based l N(x)=Nmax exp[(x-xave)2/2 x 2] l Nmax=(Ndose/[ (2 )](https://slidetodoc.com/presentation_image/2e2929d0eb26369f10ec059a71c60d36/image-15.jpg)


![Mask Thickness l Transmission through mask – T=1/2 erfc[(x-xave)/ 2 x] l To stop Mask Thickness l Transmission through mask – T=1/2 erfc[(x-xave)/ 2 x] l To stop](https://slidetodoc.com/presentation_image/2e2929d0eb26369f10ec059a71c60d36/image-18.jpg)





- Slides: 24

Lecture 9. 0 Silicon Oxidation/Diffusion/Implantation

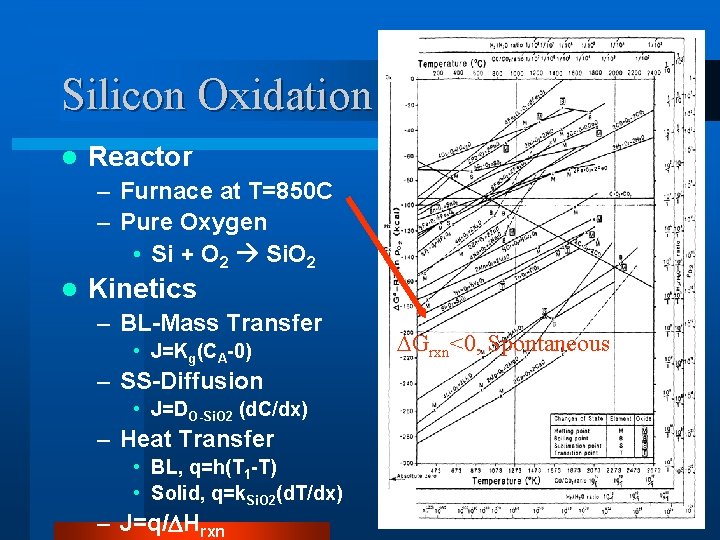
Silicon Oxidation l Reactor – Furnace at T=850 C – Pure Oxygen • Si + O 2 Si. O 2 l Kinetics – BL-Mass Transfer • J=Kg(CA-0) – SS-Diffusion • J=DO-Si. O 2 (d. C/dx) – Heat Transfer • BL, q=h(T 1 -T) • Solid, q=k. Si. O 2(d. T/dx) – J=q/ Hrxn Grxn<0, Spontaneous

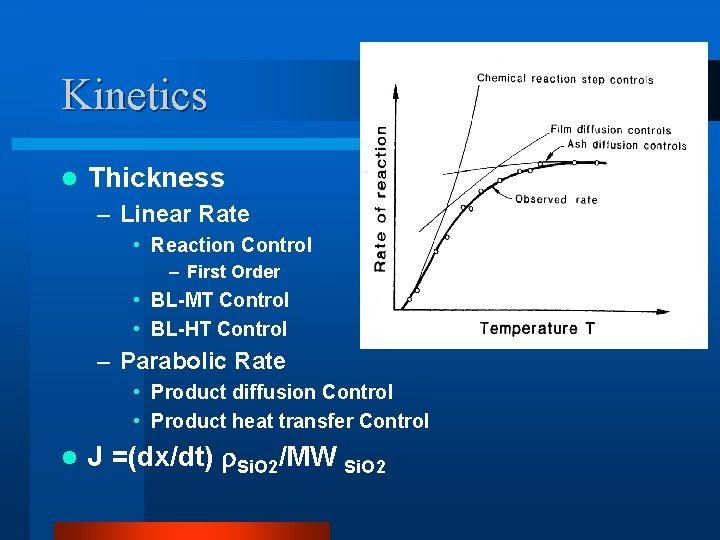
Kinetics l Thickness – Linear Rate • Reaction Control – First Order • BL-MT Control • BL-HT Control – Parabolic Rate • Product diffusion Control • Product heat transfer Control l J =(dx/dt) Si. O 2/MW Si. O 2

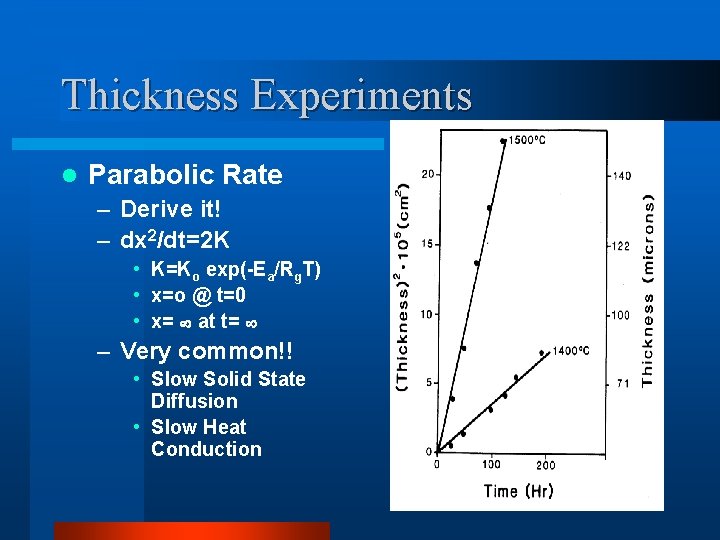
Thickness Experiments l Parabolic Rate – Derive it! – dx 2/dt=2 K • K=Ko exp(-Ea/Rg. T) • x=o @ t=0 • x= at t= – Very common!! • Slow Solid State Diffusion • Slow Heat Conduction

Field Oxide l Thick oxide – Oxygen – Steam l High Temperature Reaction

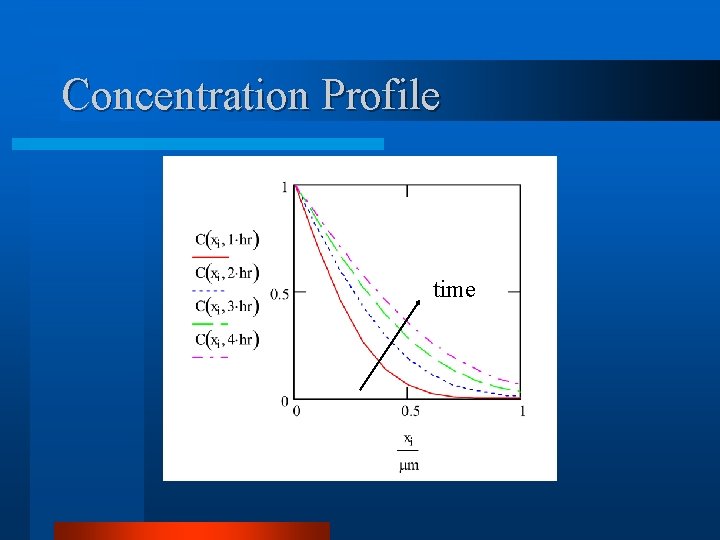
Diffusion l Deposition of B or P on surface l Heat and Hold for period of time – Solid State Diffusion – d. C/dt=D d 2 C/dx 2 • C=Co at x=0 • C=0 at x= – C=Co(1 -erf[x/ (4 Dt)]) l Etch excess B or P from surface

Concentration Profile time

Diffusion Coefficient l Self Diffusion – D*=Doexp(-Ea/Rg. T) l Diffusion of A in B • Depends on A and matrix B – DAB =(D*A XB + D*B XA) (d ln [a. A]/d ln [XA]) – d ln [a. A]/d ln [XA] = 1+ (d ln [ A]/d ln [XA]) – d ln [a. A]/d ln [XA] ~ 1 for ideal solutions • And • DAB =(D*A XB + D*B XA) = (D*A (1 -XA) + D*B XA) • Note Concentration dependence!! • DAB ~D*A when XA ~0 , the dilute solution limit – Good for dopants

Implantation l Energy Loss l Stopping of Ion – Nuclear cross section, Sn(E) – Electronic cross section, Se(E) – ρT = atomic density of target (#/cc)
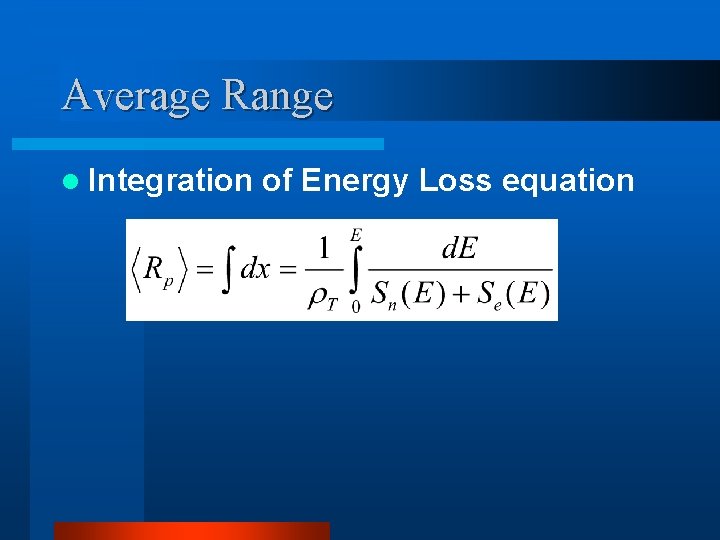
Average Range l Integration of Energy Loss equation

Implantation Create Ions in Vacuum l Accelerate in Electric Field l Impinge onto Silicon Surface l Knock out Si ion(s) l – Charge Balance l Travel deep into Silicon

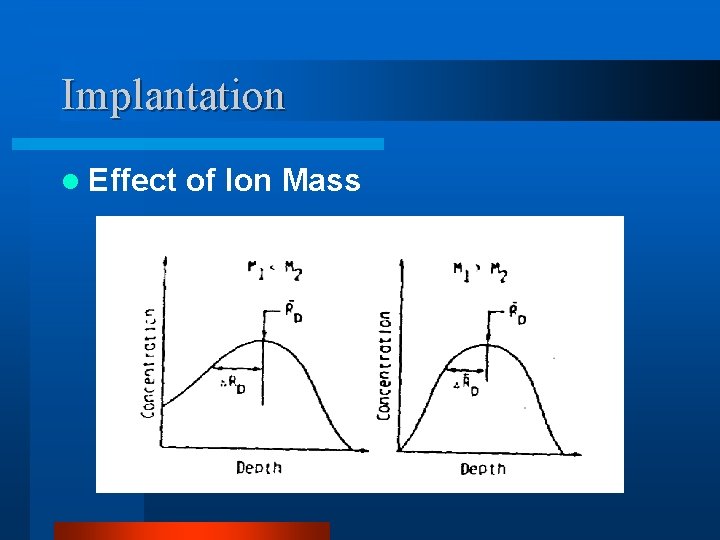
Implantation l Effect of Ion Mass

Implant Depth Increases with Energy

Implantation Straggle Increases with Energy
![Implantation Concentration Profile Probability Based l NxNmax expxxave22 x 2 l NmaxNdose 2 Implantation Concentration Profile Probability Based l N(x)=Nmax exp[(x-xave)2/2 x 2] l Nmax=(Ndose/[ (2 )](https://slidetodoc.com/presentation_image/2e2929d0eb26369f10ec059a71c60d36/image-15.jpg)
Implantation Concentration Profile Probability Based l N(x)=Nmax exp[(x-xave)2/2 x 2] l Nmax=(Ndose/[ (2 ) x])~(0. 4 Ndose/ x) l Ndose=Qdose/e l Qdose= current applied/cm 2 l σx = straggle l

Implantation Through Slit l Slit opening = a l N(x) =projected range formula l ΔR = transverse straggle

Mask Thickness l l l To effectively prevent ions penetrating in thick zone Relatively thick Oxide Protection layer Patterned Thinning (etching) of Oxide Protection layer over implantation zone Remove oxide layer with impurities inside
![Mask Thickness l Transmission through mask T12 erfcxxave 2 x l To stop Mask Thickness l Transmission through mask – T=1/2 erfc[(x-xave)/ 2 x] l To stop](https://slidetodoc.com/presentation_image/2e2929d0eb26369f10ec059a71c60d36/image-18.jpg)
Mask Thickness l Transmission through mask – T=1/2 erfc[(x-xave)/ 2 x] l To stop 99. 99% of implanted materials, T=10 -4 l Solve for x, the thickness to stop 99. 99% of ions.

Si. O 2 Mask Thickness

Si 3 N 4 Mask Thickness

Photoresist Mask Thickness

Implant Depth Increases with Energy

Diffusion of Implanted Dopants Diffusion Furnace or Laser l Heat Treatment l – Solid State Diffusion – d. C/dt = CT d/dz (DAB d. XA /dz) • C=Co(z) = CT XA(z) at z=0 • C=0 at z= – DAB =(D*A XB + D*B XA) (d ln [a. A]/d ln [XA]) – Interdiffusion or mutual diffusion coefficient

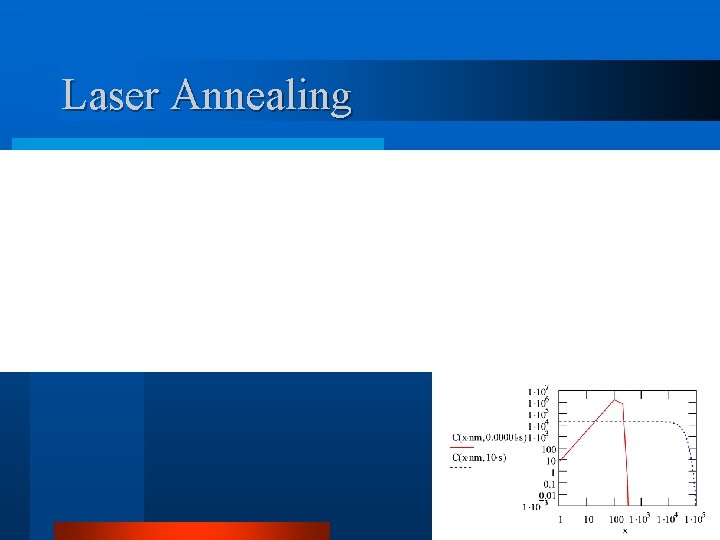
Laser Annealing