Lecture 8 n n Kmap minimization examples POS

Example: BCD increment-by-1 O 2 O 4 O 8 I 1 I 2 I

BCD increment-by-1: K-maps I 8 O 8 = I 4 I 2 I 1

Example: Two-bit multiplier P 1 P 2 P 4 P 8 A 1 A

POS minimization with K-maps n n Encircle the zeros in the map Interpret indices

Design example: Comparator A B C D AB < CD LT AB = CD

Comparator: K-maps K-map for LT K-map for EQ K-map for GT A AB CD

Comparator: Implementing EQ A B C Option 1: EQ = A'B'C'D'+A'BC'D+ABCD+AB'CD' D 5 gates

Switching networks logic blocks n Multiplexer (MUX) ¡ ¡ n Routes one of many

Multiplexers n Basic concept ¡ ¡ ¡ 2 n data inputs; n control inputs

Multiplexers: Truth tables n Two alternative truth-tables: Functional and Logical Functional truth table Example:

Multiplexers n n n I 0 I 1 2: 1 mux: Z = S

Multiplexers: Implementation 4: 1 mux 2: 1 mux I 0 S I 1 Z

Cascading multiplexers n Can form large multiplexers from smaller ones (many implementation options) 8:

Multiplexer as logic block n A 2 n: 1 mux can implement any function

Multiplexer as logic block n Can also use a 2 n-1: 1 mux to

Multiplexer as logic block n F(A, B, C, D) implemented using an 8: 1

Slides: 19

Download presentation

Lecture 8 n n K-map minimization examples POS minimization with K-map Design example "Switching network" logic blocks (multiplexers/demultiplexers) 1

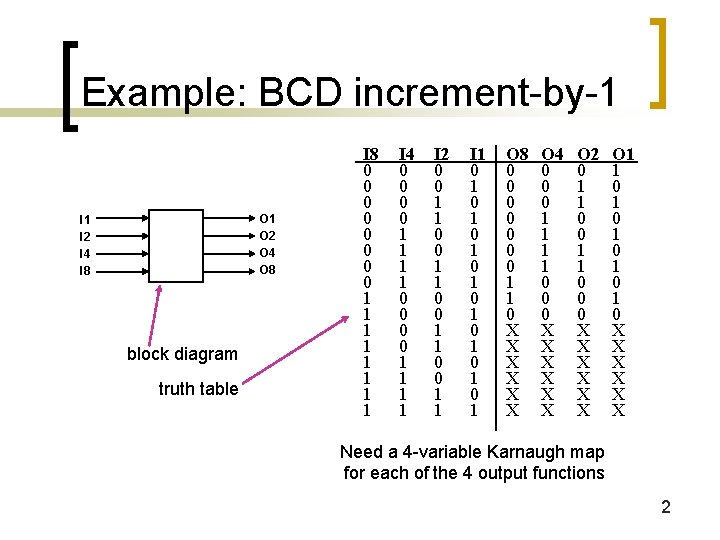
Example: BCD increment-by-1 O 2 O 4 O 8 I 1 I 2 I 4 I 8 block diagram truth table I 8 0 0 0 0 1 1 1 1 I 4 0 0 0 0 1 1 1 1 I 2 0 0 1 1 I 1 0 1 0 1 O 8 0 0 0 0 1 1 0 X X X O 4 0 0 0 1 1 0 0 0 X X X O 2 0 1 1 0 0 0 X X X O 1 1 0 1 0 1 0 X X X Need a 4 -variable Karnaugh map for each of the 4 output functions 2

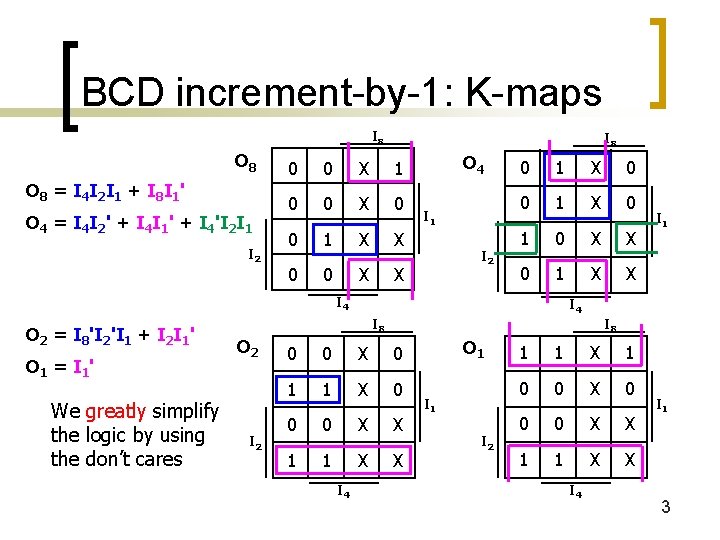
BCD increment-by-1: K-maps I 8 O 8 = I 4 I 2 I 1 + I 8 I 1 ' O 4 = I 4 I 2' + I 4 I 1' + I 4'I 2 I 1 I 2 I 8 0 0 X 1 0 0 X 0 0 1 X X 0 0 X X O 4 I 1 I 2 0 1 X 0 1 0 X X 0 1 X X I 4 O 2 = I 8'I 2'I 1 + I 2 I 1' O 1 = I 1 ' We greatly simplify the logic by using the don’t cares I 4 I 8 O 2 I 8 0 0 X 0 1 1 X 0 0 0 X X 1 1 X X I 4 I 1 O 1 I 2 1 1 X 1 0 0 X 0 0 0 X X 1 1 X X I 4 I 1 3

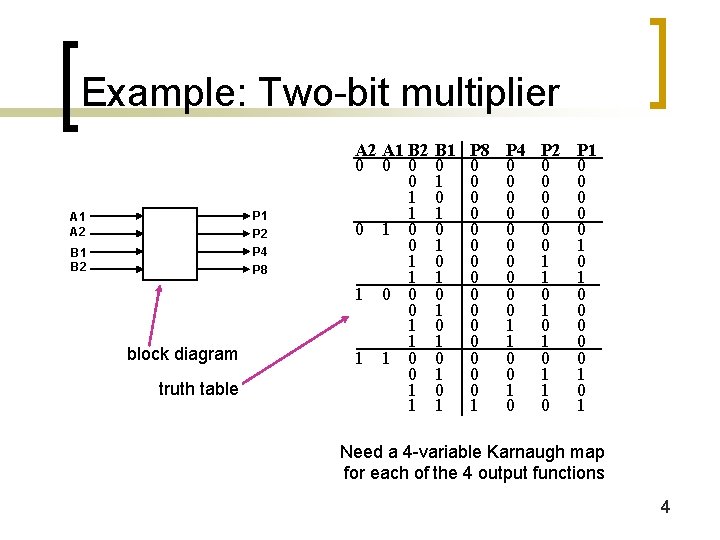
Example: Two-bit multiplier P 1 P 2 P 4 P 8 A 1 A 2 B 1 B 2 block diagram truth table A 2 A 1 B 2 0 0 1 1 1 0 0 0 1 1 B 1 0 1 0 1 P 8 0 0 0 0 1 P 4 0 0 0 0 0 1 1 0 0 1 0 P 2 0 0 0 1 1 0 1 0 1 1 0 P 1 0 0 0 0 0 1 0 1 Need a 4 -variable Karnaugh map for each of the 4 output functions 4

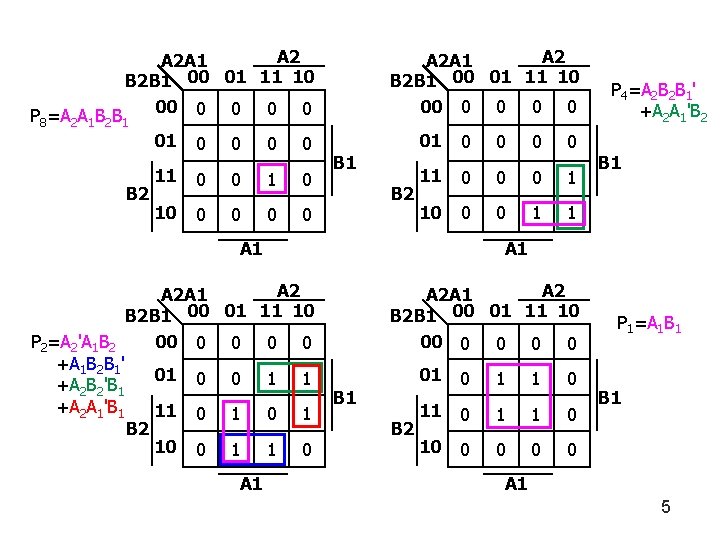
A 2 A 2 A 1 B 2 B 1 00 01 11 10 00 0 0 P 8=A 2 A 1 B 2 B 1 01 0 0 B 2 11 0 0 10 0 0 A 2 A 1 B 2 B 1 00 01 11 10 00 0 0 B 1 B 2 01 0 0 11 0 0 0 1 1 A 1 A 2 A 1 B 2 B 1 00 01 11 10 00 0 0 P 2=A 2'A 1 B 2 +A 1 B 2 B 1' 01 0 0 1 1 +A 2 B 2'B 1 +A 2 A 1'B 1 11 0 1 B 2 10 0 1 1 0 A 1 P 4=A 2 B 2 B 1' +A 2 A 1'B 2 B 1 A 2 A 2 A 1 B 2 B 1 00 01 11 10 00 0 0 B 2 01 0 10 0 0 P 1=A 1 B 1 A 1 5

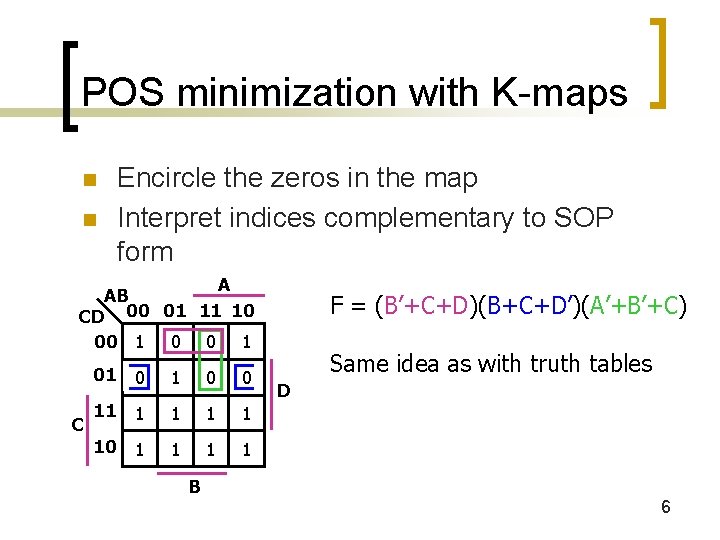
POS minimization with K-maps n n Encircle the zeros in the map Interpret indices complementary to SOP form A AB CD 00 01 11 10 00 1 0 0 1 C 01 0 0 11 1 1 10 1 1 F = (B’+C+D)(B+C+D’)(A’+B’+C) Same idea as with truth tables D B 6

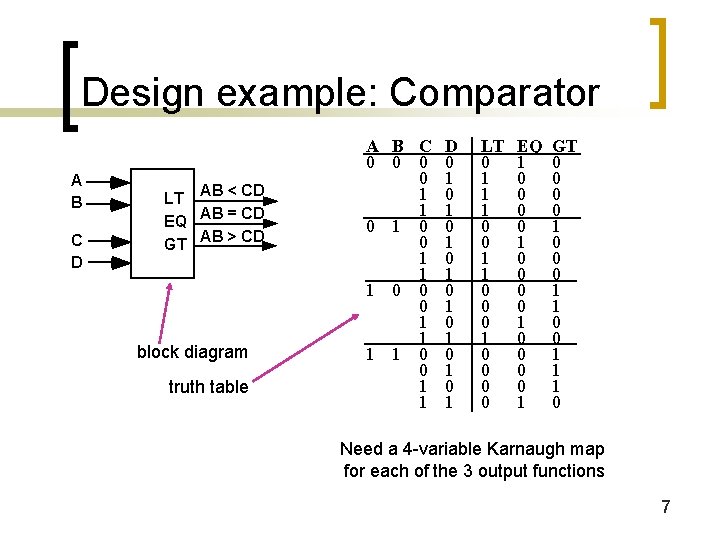
Design example: Comparator A B C D AB < CD LT AB = CD EQ AB > CD GT block diagram truth table A B C 0 0 1 1 1 0 0 0 1 1 D 0 1 0 1 LT 0 1 1 1 0 0 0 1 0 0 EQ 1 0 0 0 0 1 GT 0 0 1 0 0 0 1 1 1 0 Need a 4 -variable Karnaugh map for each of the 3 output functions 7

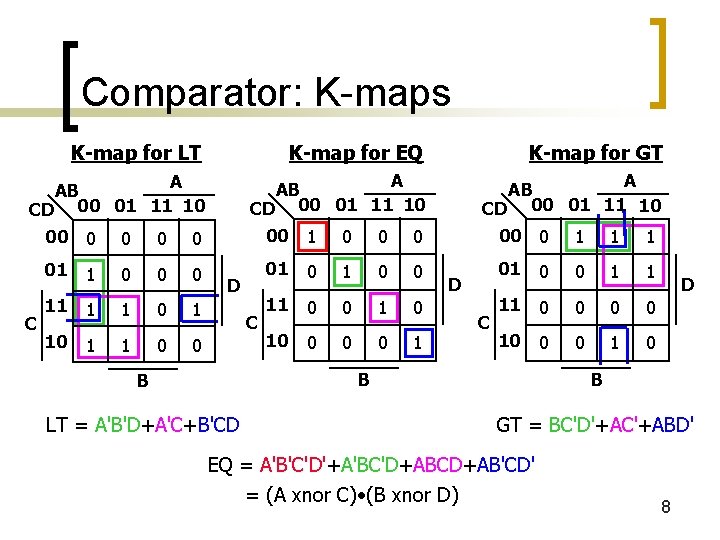
Comparator: K-maps K-map for LT K-map for EQ K-map for GT A AB CD 00 01 11 10 C 00 0 0 00 1 0 00 0 1 1 1 0 0 0 01 0 0 1 1 1 0 1 11 0 0 10 1 1 0 0 10 0 1 10 0 0 1 0 D C B B LT = A'B'D+A'C+B'CD D B GT = BC'D'+AC'+ABD' EQ = A'B'C'D'+A'BC'D+ABCD+AB'CD' = (A xnor C) • (B xnor D) 8

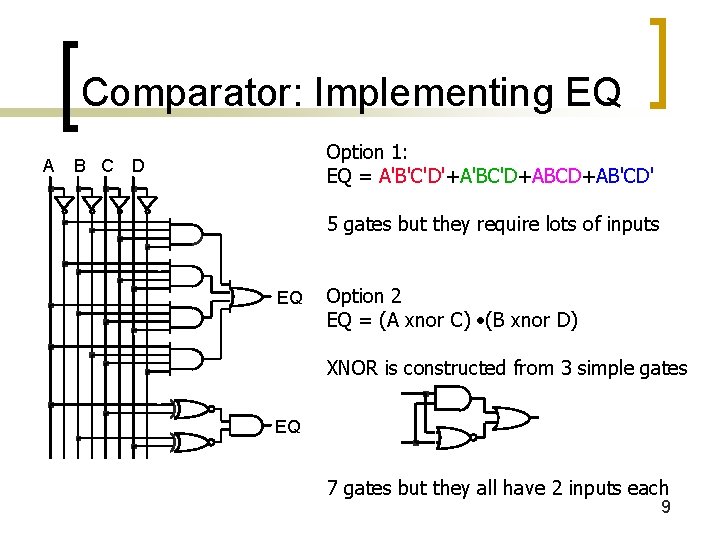
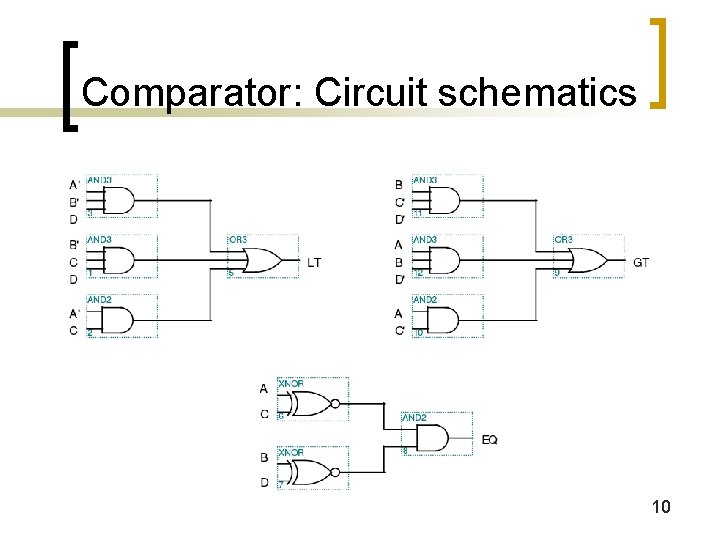
Comparator: Implementing EQ A B C Option 1: EQ = A'B'C'D'+A'BC'D+ABCD+AB'CD' D 5 gates but they require lots of inputs EQ Option 2 EQ = (A xnor C) • (B xnor D) XNOR is constructed from 3 simple gates EQ 7 gates but they all have 2 inputs each 9

Comparator: Circuit schematics 10

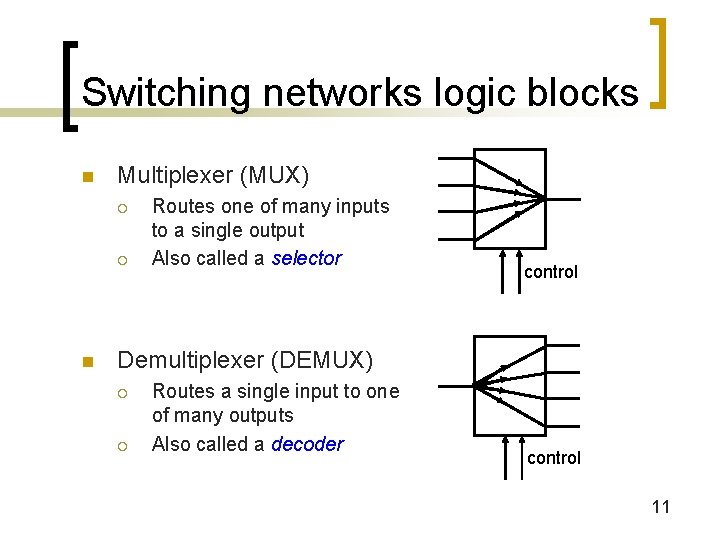
Switching networks logic blocks n Multiplexer (MUX) ¡ ¡ n Routes one of many inputs to a single output Also called a selector control Demultiplexer (DEMUX) ¡ ¡ Routes a single input to one of many outputs Also called a decoder control 11

Multiplexers n Basic concept ¡ ¡ ¡ 2 n data inputs; n control inputs ("selects"); 1 output Connects one of 2 n inputs to the output “Selects” decide which input connects to output 12

Multiplexers: Truth tables n Two alternative truth-tables: Functional and Logical Functional truth table Example: A 2: 1 Mux Z = SIn 1 + S'Ino S 0 1 I 0 Z S I 1 Z In 0 In 1 Logical truth table In 1 0 0 1 1 In 0 0 0 1 1 S 0 1 0 1 Z 0 0 1 1 1 13

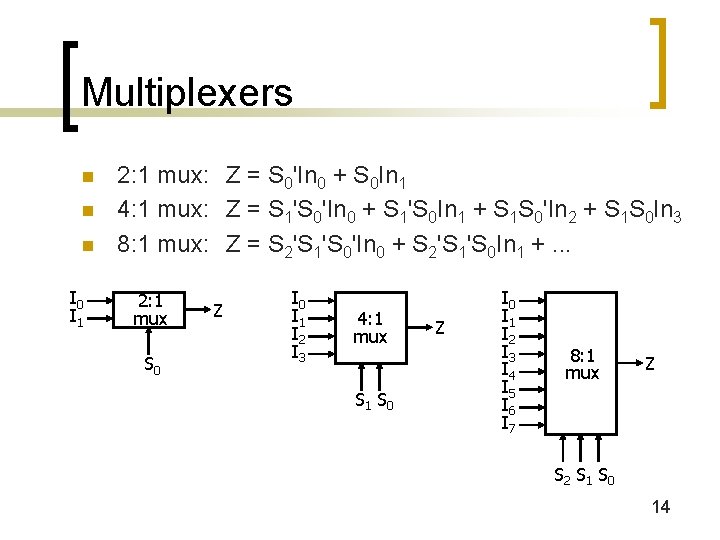
Multiplexers n n n I 0 I 1 2: 1 mux: Z = S 0'In 0 + S 0 In 1 4: 1 mux: Z = S 1'S 0'In 0 + S 1'S 0 In 1 + S 1 S 0'In 2 + S 1 S 0 In 3 8: 1 mux: Z = S 2'S 1'S 0'In 0 + S 2'S 1'S 0 In 1 +. . . 2: 1 mux S 0 Z I 0 I 1 I 2 I 3 4: 1 mux S 1 S 0 Z I 0 I 1 I 2 I 3 I 4 I 5 I 6 I 7 8: 1 mux Z S 2 S 1 S 0 14

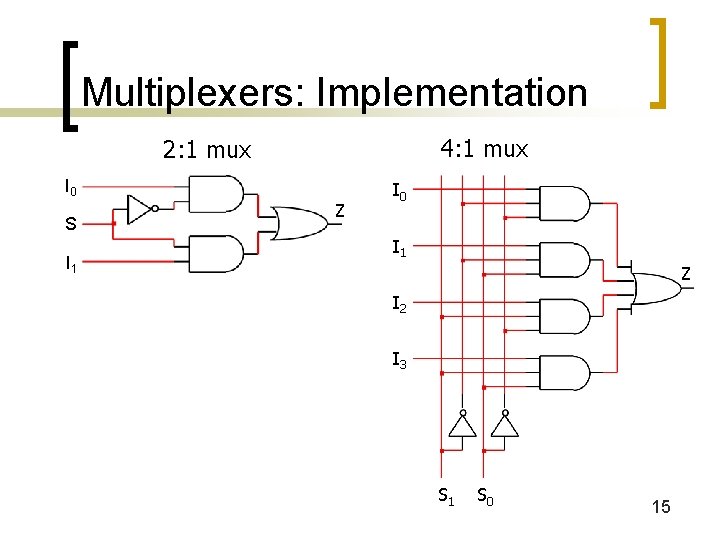
Multiplexers: Implementation 4: 1 mux 2: 1 mux I 0 S I 1 Z I 0 I 1 Z I 2 I 3 S 1 S 0 15

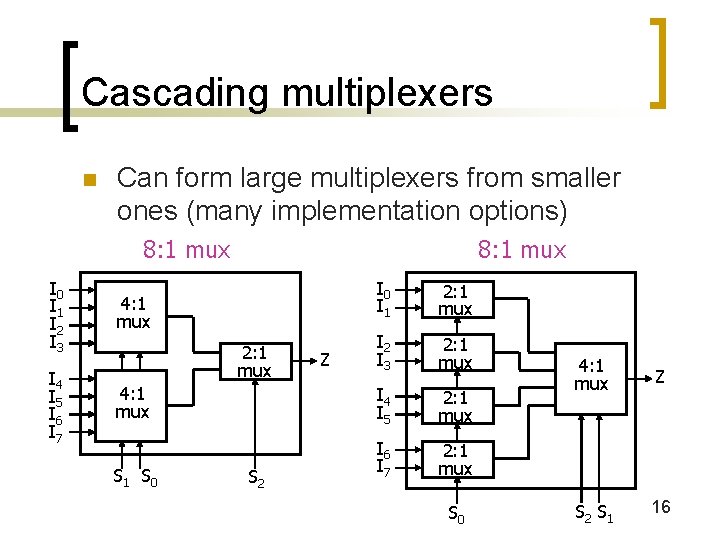
Cascading multiplexers n Can form large multiplexers from smaller ones (many implementation options) 8: 1 mux I 0 I 1 I 2 I 3 I 4 I 5 I 6 I 7 8: 1 mux 4: 1 mux 2: 1 mux 4: 1 mux S 1 S 0 S 2 Z I 0 I 1 2: 1 mux I 2 I 3 2: 1 mux I 4 I 5 2: 1 mux I 6 I 7 2: 1 mux S 0 4: 1 mux Z S 2 S 1 16

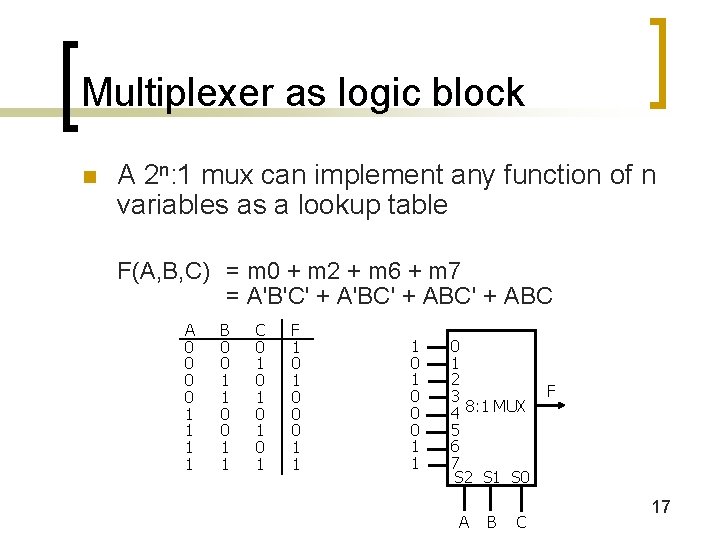
Multiplexer as logic block n A 2 n: 1 mux can implement any function of n variables as a lookup table F(A, B, C) = m 0 + m 2 + m 6 + m 7 = A'B'C' + A'BC' + ABC A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 F 1 0 1 0 0 0 1 1 0 1 2 3 4 8: 1 MUX 5 6 7 S 2 S 1 S 0 A B C F 17

Multiplexer as logic block n Can also use a 2 n-1: 1 mux to implement a function of n variables ¡ ¡ ¡ (n-1) mux control variables S 0 – Sn– 2 One data variable Sn-1 Four possible values for each data input: 0, 1, Sn -1, Sn-1' A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 F 1 0 0 0 1 1 C' C' 0 1 0 1 2 4: 1 MUX 3 S 1 S 0 A B F 18

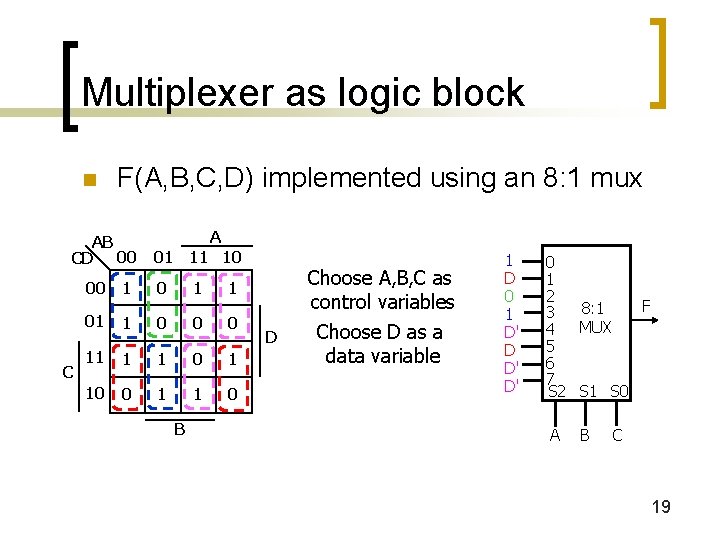
Multiplexer as logic block n F(A, B, C, D) implemented using an 8: 1 mux AB CD 00 C A 01 11 10 00 1 1 01 1 0 0 0 11 1 1 0 1 10 0 1 1 0 B Choose A, B, C as control variables D Choose D as a data variable 1 D 0 1 D' D' 0 1 2 F 8: 1 3 MUX 4 5 6 7 S 2 S 1 S 0 A B C 19