Lecture 8 Greedy Approach Minimum spanning tree How

Lecture 8 Greedy Approach • Minimum spanning tree • How to design greedy algorithms

Roadmap • Minimum spanning tree • How to design greedy algorithms ‣ Change-making problem ‣ Activity selection problem ‣ Huffman code ‣ Knapsack problem

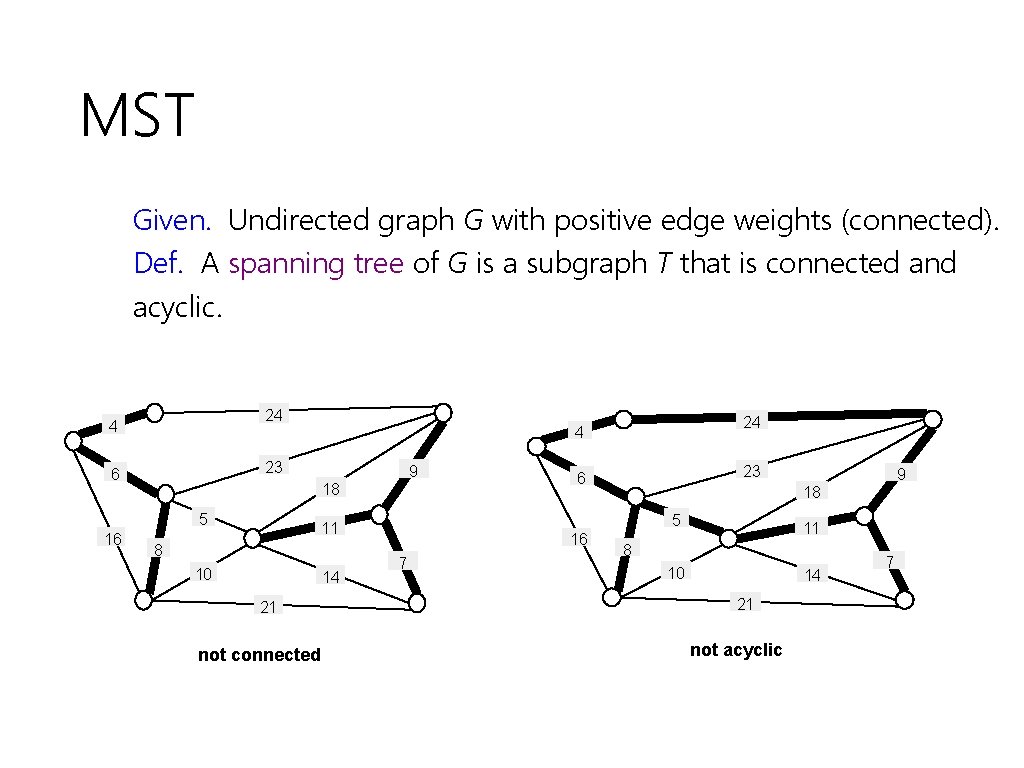
MST Given. Undirected graph G with positive edge weights (connected). Def. A spanning tree of G is a subgraph T that is connected and acyclic. 24 4 23 6 16 9 18 5 24 4 10 14 21 not connected 16 7 9 18 5 11 8 23 6 11 8 10 14 21 not acyclic 7

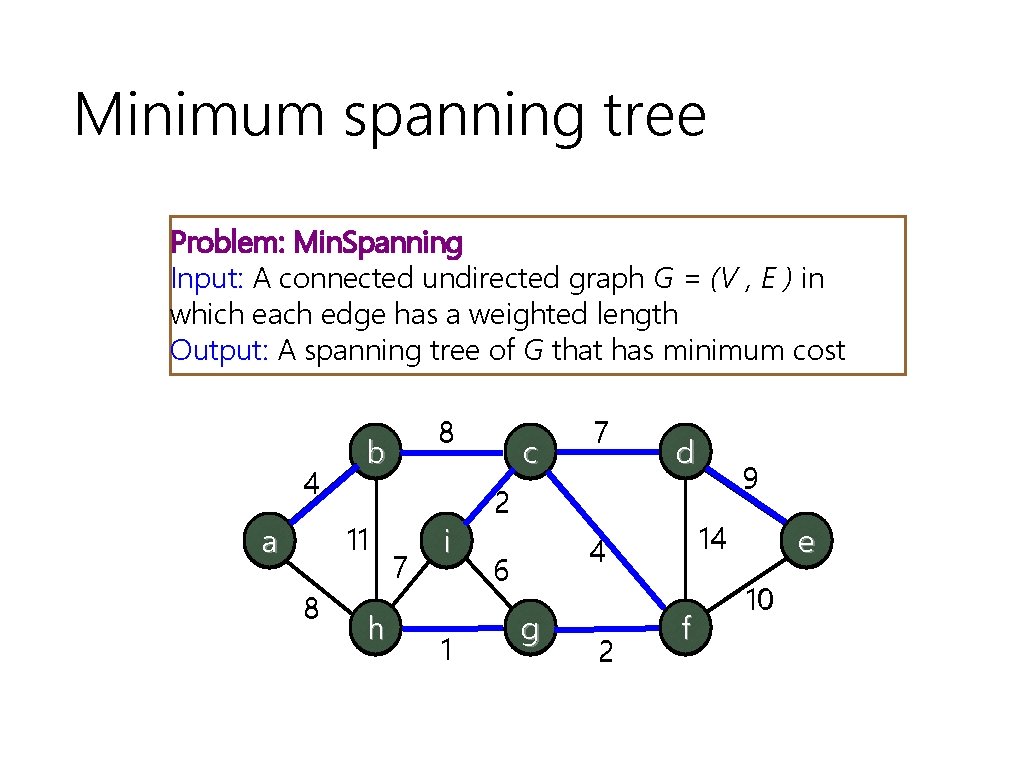
Minimum spanning tree Problem: Min. Spanning Input: A connected undirected graph G = (V , E ) in which each edge has a weighted length Output: A spanning tree of G that has minimum cost 4 b 11 a 8 8 h 7 i 1 c 7 d 2 14 4 6 g 2 9 f e 10

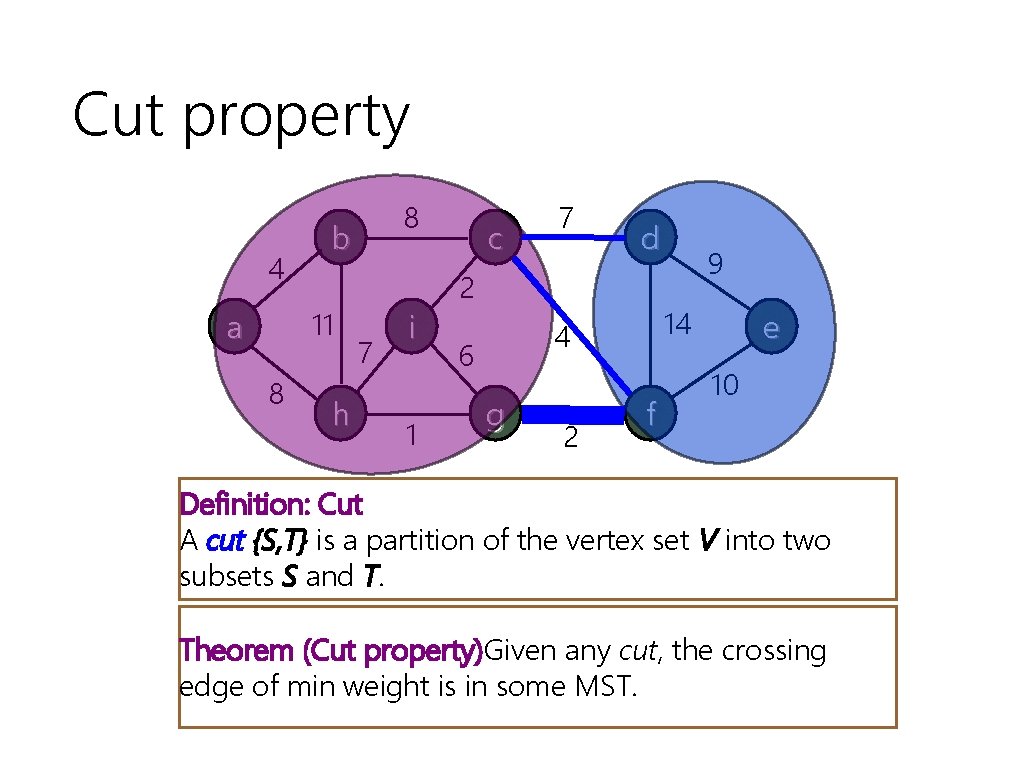
Cut property 4 b 11 a 8 8 h 7 i 1 c 7 d 2 14 4 6 g 2 9 f e 10 Definition: Cut A cut {S, T} is a partition of the vertex set V into two subsets S and T. Theorem (Cut property)Given any cut, the crossing edge of min weight is in some MST.

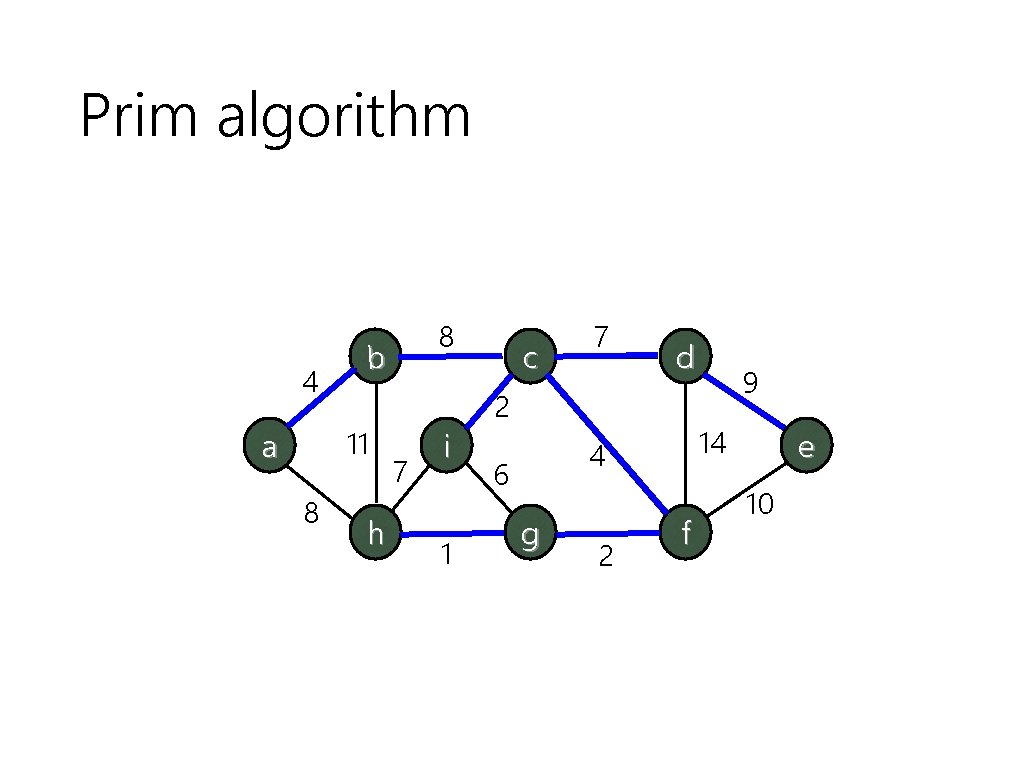
Correctness Theorem Kruskal algorithm and Prim algorithm correctly find a minimum cost spanning tree.

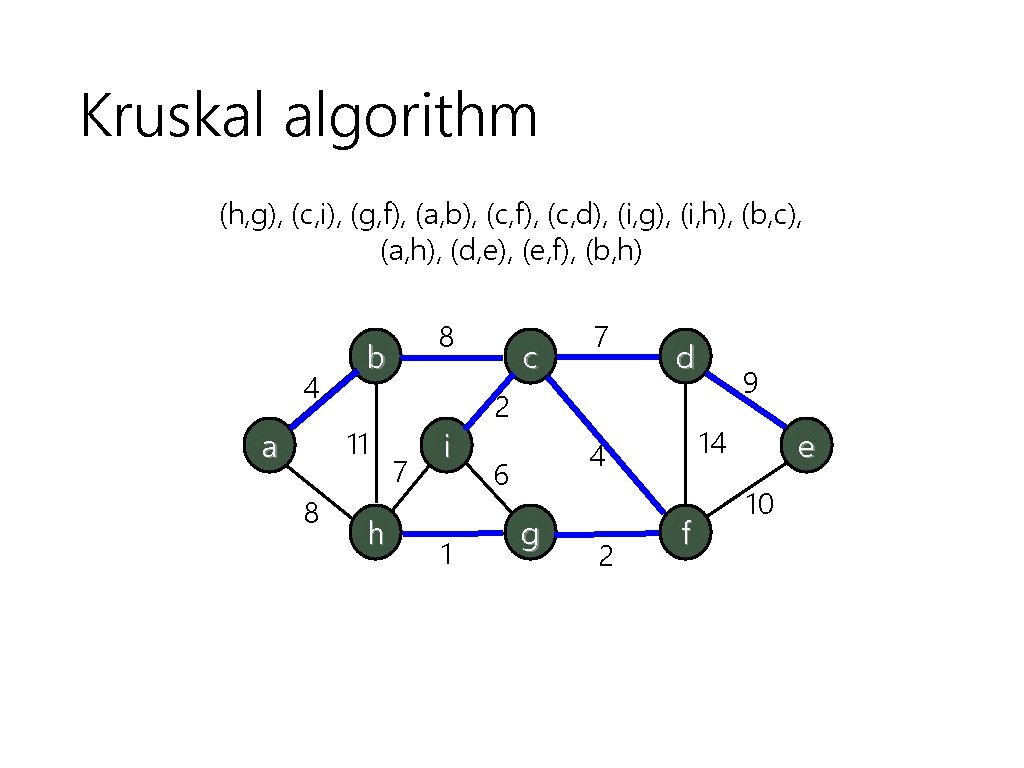
Kruskal algorithm (h, g), (c, i), (g, f), (a, b), (c, f), (c, d), (i, g), (i, h), (b, c), (a, h), (d, e), (e, f), (b, h) 4 b 11 a 8 8 h 7 i 1 c 7 d 2 14 4 6 g 2 9 f e 10

Kruskal algorithm ) m g o l Θ(m

Prim algorithm 4 b 11 a 8 8 h 7 i 1 c 7 d 2 14 4 6 g 2 9 f e 10

2) Θ(n ) n g o l m ( Θ : p a He

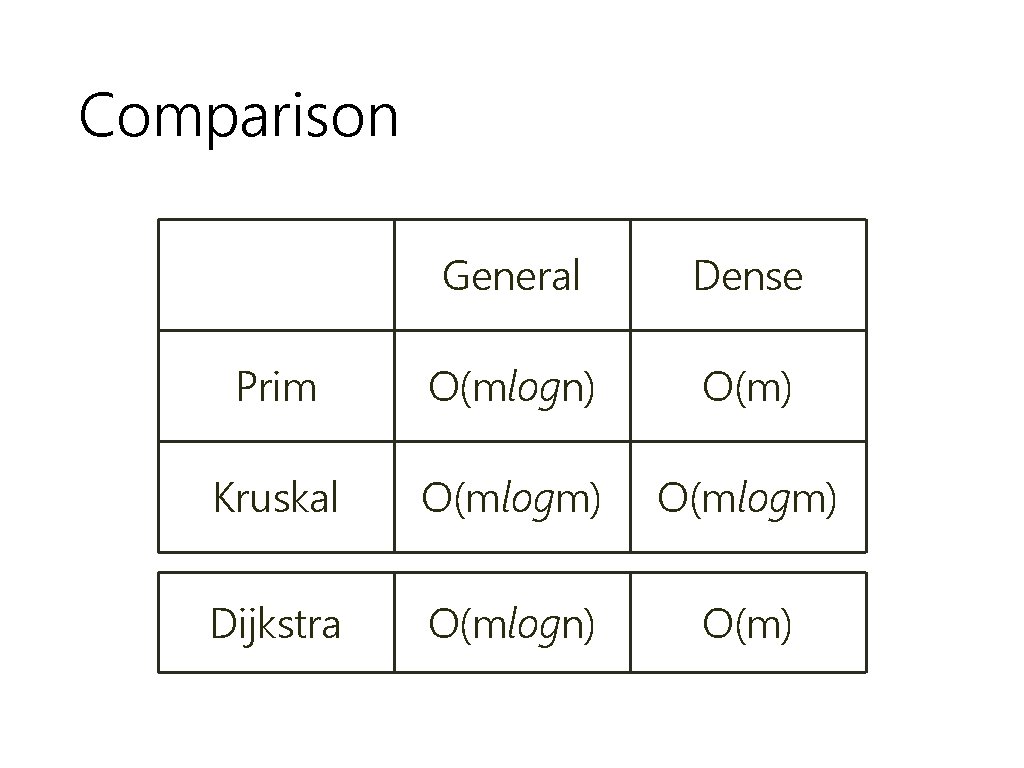
Comparison General Dense Prim O(mlogn) O(m) Kruskal O(mlogm) Dijkstra O(mlogn) O(m)

Comparison Kruskal demo Prim demo

Greed is good. Greed, for lack of a better word, is good. Greed is right. Greed works. Greed clarifies, cuts through, and captures, the essence of the evolutionary spirit. Greed, in all of its forms; greed for life, for money, for love, knowledge, has marked the upward surge of mankind and greed, you mark my words, will not only save Teldar Paper, but that other malfunctioning corporation called the U. S. A. ---- Michael Douglas, Wall Street

Greedy approach A greedy algorithm always makes the choice that looks best at the moment. locally optimal choices --> a globally optimal solution. Greedy algorithms DO NOT always yield optimal solutions, but for many problems they do. Dijkstra algorithm, Prim algorithm, Kruskal algorithm

Where are we? • Minimum spanning tree • How to design greedy algorithms ‣ Change-making problem ‣ Activity selection problem ‣ Huffman code ‣ Knapsack problem

Change making Problem: Change. Making Input: an integer m and a coin system a 1, a 2, . . . , an Output: the minimum number of coins needed 1 2 5 1 2 7 10 16?

Activity selection problem Problem: Activity. Selection Input: a set S = {a 1, a 2, . . . , an} of n proposed activities, each ai has a starting time si and a finishing time fi with 0 ≤ si < fi <∞ Output: A maximum-size subset of compatible activities

Activity-selection Theorem Consider any nonempty subproblem Sk, and let am be an activity in Sk with the earliest finish time. Then am is included in some maximum-size subset of mutually compatible activities of Sk.

Huffman code Robert Fano Claude Shannon David Huffman

Ambiguity Morse code: SOS ? V 7 ? IAMIE ? EEWNI ?

Prefix-free code Prefix code: no codeword is a prefix of some other codeword. Use a binary tree to represent a prefix-free code.

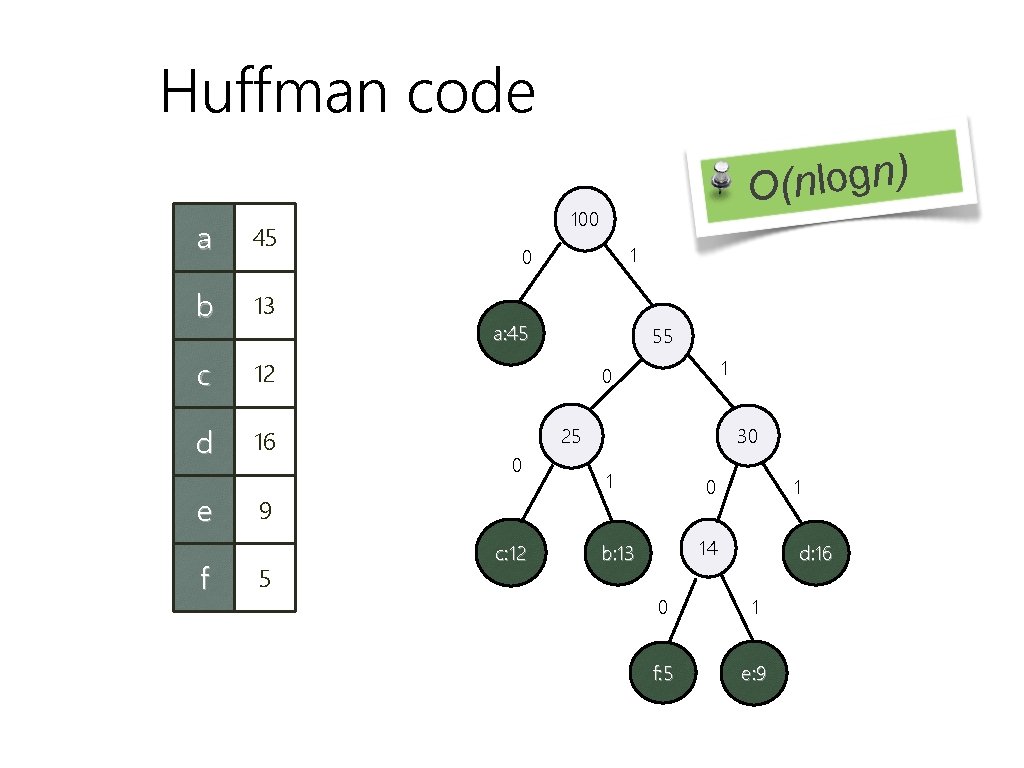
Huffman code Frequency Fixed-length Huffman code a b c d e f 45 13 12 16 9 5 000 001 010 011 100 101 100 111 1100 100, 000 characters, Fixed length code: 300, 000 bits Huffman code: 224, 000 bits

Huffman code a 45 b 13 c 12 d 16 e f 100 1 0 a: 45 55 1 0 30 25 0 9 5 ) n g o l n ( O c: 12 1 0 1 14 b: 13 d: 16 0 1 f: 5 e: 9

Huffman code

Correctness Lemma Let x and y be two characters in C having the lowest frequencies. Then there exists an optimal prefix code for C in which x and y have the same length and differ only in the last bit. Lemma Let x and y be two characters in C having the lowest frequencies. C’ = C-{x, y} +{z}, fz= fx + fy. If T’ is an optimal prefix code for C’, then T=T’+{(z, x), (z, y)} is an optimal prefix code for C. Theorem Procedure HUFFMAN produces an optimal prefix code.

Knapsack problem Problem: Knapsack Input: A set of items U = {u 1, . . . , un} with sizes s 1, s 2, . . . , sn and values v 1, v 2, . . . , vn and a knapsack capacity C Output: The maximum value that can be put into the knapsack

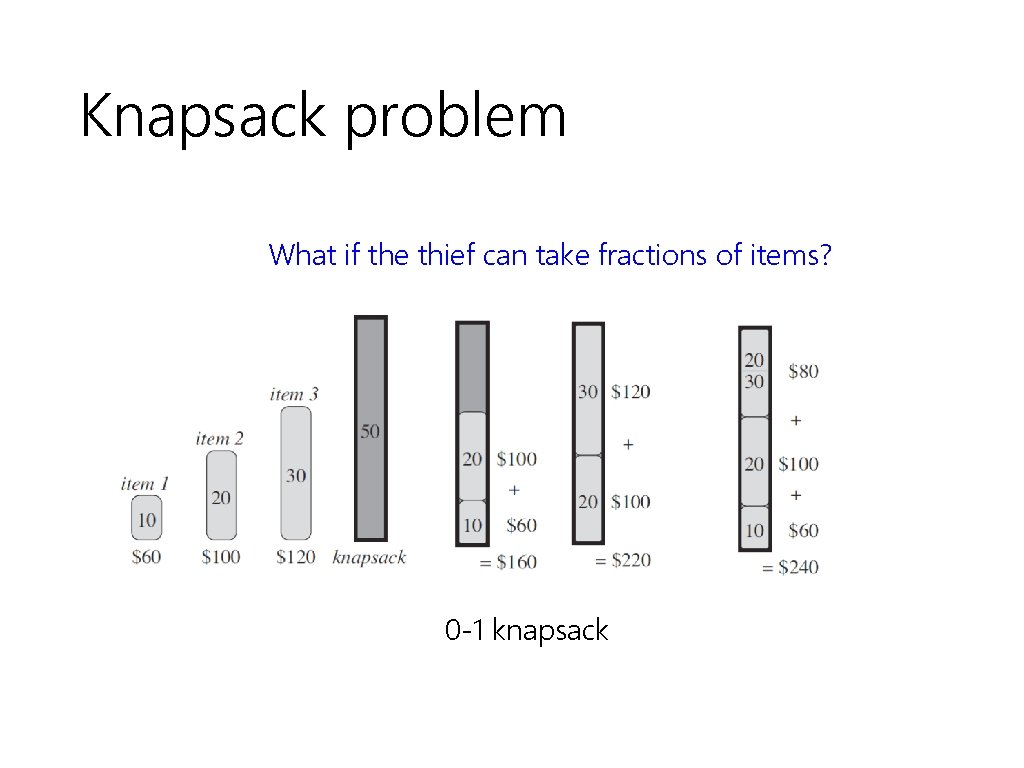
Knapsack problem What if the thief can take fractions of items? 0 -1 knapsack

Conclusion • Minimum spanning tree • How to design greedy algorithms ‣ Change-making problem ‣ Activity selection problem ‣ Huffman code ‣ Knapsack problem