Lecture 8 Dispatch Rules J Christopher Beck 2005

Lecture 8: Dispatch Rules © J. Christopher Beck 2005 1

Outline n What is a Dispatch Rule? n n 1 -machine Problems n n WSPT, EDD, MS, ATC Parallel Machines n n Static & dynamic LPT Applying dispatch rules to a big JSP © J. Christopher Beck 2005 2

Dispatch Rules n Create a queue of operations for each resource n n include all operations that can execute at the current time Whenever a machine becomes free: n n n update queues rank activities (based on a [simple] rule) schedule highest priority activity © J. Christopher Beck 2005 3

Dispatch Rules for JSP J 0 J 1 J 2 © J. Christopher Beck 2005 4

Dispatch Rules for JSP J 0 J 1 J 2 © J. Christopher Beck 2005 5

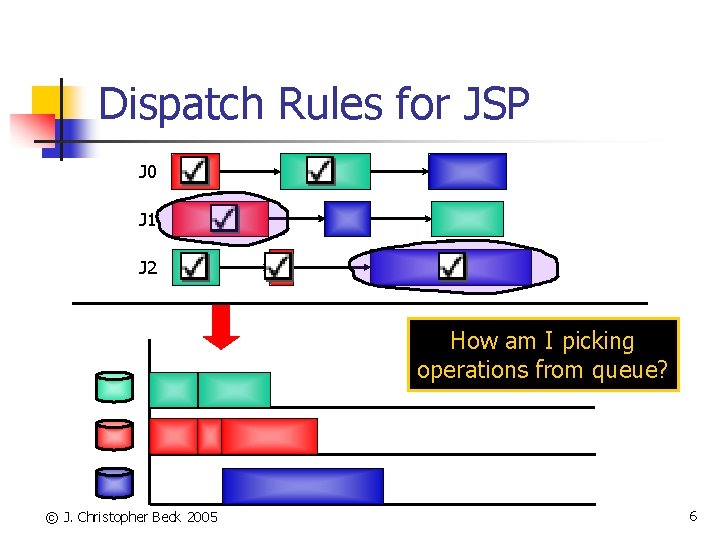
Dispatch Rules for JSP J 0 J 1 J 2 How am I picking operations from queue? © J. Christopher Beck 2005 6

Dispatch Rules for JSP J 0 J 1 J 2 © J. Christopher Beck 2005 7

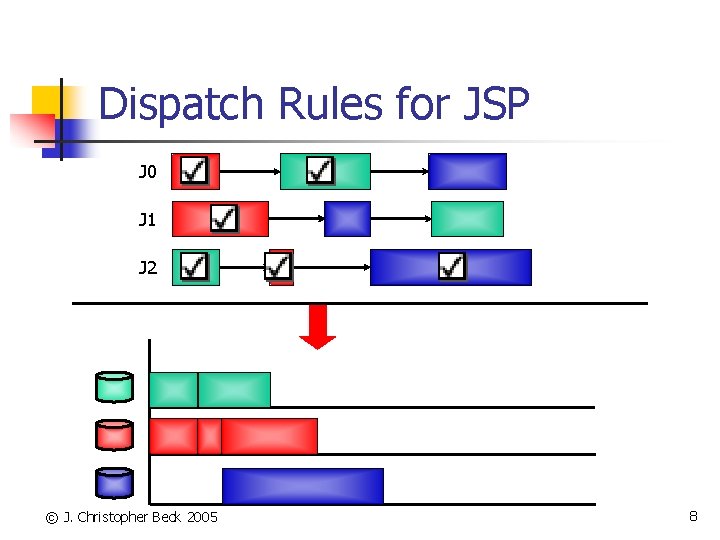
Dispatch Rules for JSP J 0 J 1 J 2 © J. Christopher Beck 2005 8

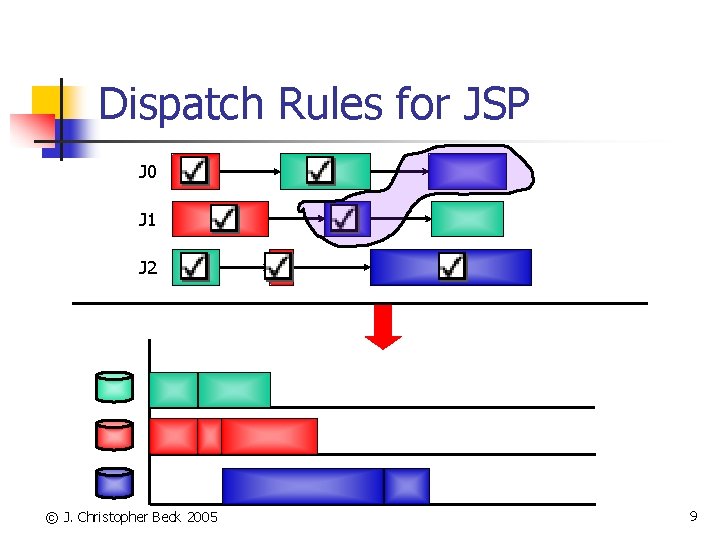
Dispatch Rules for JSP J 0 J 1 J 2 © J. Christopher Beck 2005 9

Dispatch Rules for JSP J 0 J 1 J 2 © J. Christopher Beck 2005 10

Dispatch Rules for JSP J 0 J 1 J 2 How did I pick operations? © J. Christopher Beck 2005 11

Dispatch Rules n Create a queue of operations for each resource n n include all operations that can execute at the current time Whenever a machine becomes free: n n n update queues rank activities (based on a [simple] rule) schedule highest priority activity © J. Christopher Beck 2005 12

1 -Machine Problem & WSPT n n rj = 0, dj = ∞, obj = min wj. Cj Weighted Shortest Processing Time (WSPT) results in optimal schedule n n Order operations in decreasing order of wj/pj Bonus question: prove that WSPT finds the optimal schedule for min wj. Cj © J. Christopher Beck 2005 13

1 -Machine Problem & WSPT p 1 = 10 w 1 = 1 n n p 2 = 2 w 2 = 2 p 3 = 5 w 3 = 0 p 4 = 7 w 3 = 3 Use WSPT to find min wj. Cj schedule Find min Cmax schedule n Does WSPT find optimal schedule if obj = min Cmax? © J. Christopher Beck 2005 14

1 -Machine Problem & EDD n Different problem n n n rj = 0, obj = min Lmax Each job has its own dj Earliest Due Date (EDD) results in optimal schedule n Order operations in increasing order of dj © J. Christopher Beck 2005 15

WSPT & EDD are Static n Static = basis for ordering operations does not change based on scheduling decisions n n You can sort all operations once Dynamic = scheduling decisions change the order of remaining operations n You need to re-sort operations in queue (potentially) after every decision © J. Christopher Beck 2005 16

Minimum Slack is Dynamic n n 1 -machine, rj = 0, obj = min Lmax Minimum Slack (MS) orders operations at time t in descending order of: n n max(dj – pj – t, 0) MS does not guarantee optimal schedule Question: can you find a 1 -machine problem instance where MS doesn’t find the optimal? © J. Christopher Beck 2005 n 17

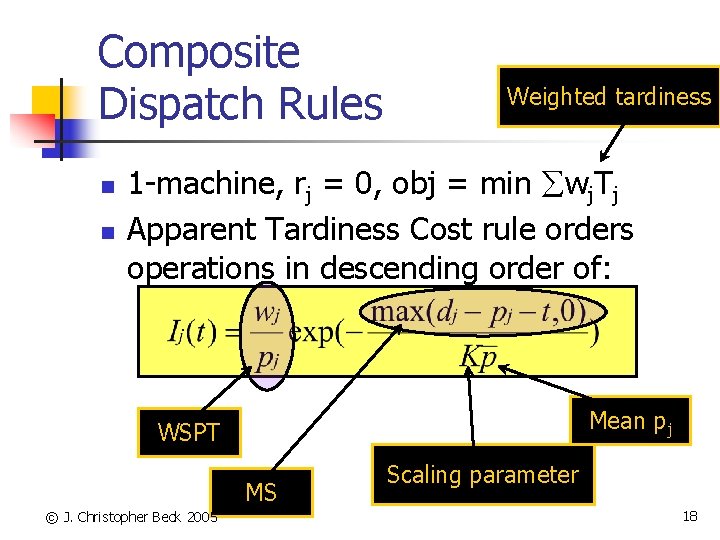
Composite Dispatch Rules n n Weighted tardiness 1 -machine, rj = 0, obj = min wj. Tj Apparent Tardiness Cost rule orders operations in descending order of: Mean pj WSPT MS © J. Christopher Beck 2005 Scaling parameter 18

Good Questions n n Given description of a 1 -machine problem which dispatch rule would you use and why? Given a 1 -machine problem, produce a schedule using dispatch rule X (show each decision)? n X = WSPT, EDD, MS, ATC, or a dispatching rule (with a given definition) © J. Christopher Beck 2005 19

Parallel Machines n n n Like 1 -machine but you have a set of machines and operations can go on any machine Can apply dispatch rules without any optimality guarantee LPT: Longest Processing Time first n pick operations in descending order of processing time © J. Christopher Beck 2005 20

Q 5. 3, p 110 n n 6 identical, unary capacity machines in parallel Compute makespan using LPT jobs 1 2 3 4 5 6 7 8 9 10 11 12 13 pj 7 8 8 9 9 10 10 11 11 6 6 6 7 © J. Christopher Beck 2005 21

JSP n Apply the following dispatch rules to the problem from the last lecture: n n SPT MS © J. Christopher Beck 2005 Activities Jobs 1 2 3 4 1 M 1, 9 M 2, 8 M 3, 4 M 4, 4 2 M 1, 5 M 2, 6 M 4, 3 M 3, 6 3 M 3, 10 M 1, 4 M 2, 9 M 4, 2 22