Lecture 8 Chapter 4 Syntax Analysis Practice Context

Lecture # 8 Chapter # 4: Syntax Analysis

Practice Context Free Grammars a) CFG generating alternating sequence of 0’s and 1’s b) CFG in which no consecutive b’s can occur but consecutive a’s can occur c) CFG for the following language: L(G)= {an b 2 n | n>=0}

Practice Answers a) S 0 A | 1 B A 1 B | 0 B 0 A | 1 b) S a. S | b. T |a |b T a. S | a c) S a. Sbb | є

Example • Design a CFG for the language L(G)= {0 n 1 m | n <> m} There are two cases: – For n>m – For n<m – Write two separate set of rules and combine them

Example • For n>m S 1 AB B 0 A 1 | Є A 0 A | 0 For n<m S 2 XY X 0 X 1 | Є Y 1 Y | 1 Combining both: S S 1 | S 2

Practice CFG • Design a CFG for the language L(G)= {0 i 1 j 2 k| i=j or j=k} There are two cases: – For i=j – For j=k – Write two separate set of rules and combine them

Solution of Practice • For i=j S 1 AB A 0 A 1 | ε B 2 B | ε For j=k S 2 XY X 0 X | ε Y 1 Y 2 | ε Combining both: S S 1 | S 2

Derivations • The one-step derivation is defined by A where A is a production in the grammar • In addition, we define – – is leftmost lm if does not contain a nonterminal is rightmost rm if does not contain a nonterminal Transitive closure * (zero or more steps) Positive closure + (one or more steps) • The language generated by G is defined by L(G) = {w T* | S + w}

Derivation (Example) Grammar G = ({E}, {+, *, (, ), -, id}, P, E) with productions P = E E+E E E*E E (E) E -E E id Example derivations: E - id E rm E + id rm id + id E * E E * id + id E + id * id + id 9

Example • For the given grammar derive the string 9 -5+2 using Left most derivation Then derive the same string using Right most derivation

Example Grammar Context-free grammar for simple expressions: G = <{list, digit}, {+, -, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, P, list> with productions P = list + digit list - digit list digit 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 11

Derivation for the Example Grammar list + digit list - digit + digit 9 - 5 + digit 9 -5+2 This is an example leftmost derivation, because we replaced the leftmost nonterminal (underlined) in each step. Likewise, a rightmost derivation replaces the rightmost nonterminal in each step 12

Chomsky Hierarchy: Language Classification • A grammar G is said to be – Regular if it is right linear where each production is of the form A w. B or A w or left linear where each production is of the form A Bw or A w – Context free if each production is of the form A where A N and (N T)* – Context sensitive if each production is of the form A where A N, , , (N T)*, | | > 0 – Unrestricted 13

Chomsky Hierarchy L(regular) L(context free) L(context sensitive) L(unrestricted) Where L(T) = { L(G) | G is of type T } That is: the set of all languages generated by grammars G of type T Examples: Every finite language is regular! (construct a FSA for strings in L(G)) L 1 = { anbn | n 1 } is context free L 2 = { anbncn | n 1 } is context sensitive 14

Parse Trees • The root of the tree is labeled by the start symbol • Each leaf of the tree is labeled by a terminal (=token) or • Each interior node is labeled by a nonterminal • If A X 1 X 2 … Xn is a production, then node A has immediate children X 1, X 2, …, Xn where Xi is a (non)terminal or ( denotes the empty string) 15

Parse Tree for the Example Grammar Parse tree of the string 9 -5+2 using grammar G list digit 9 - 5 + 2 The sequence of leafs is called the yield of the parse tree 16

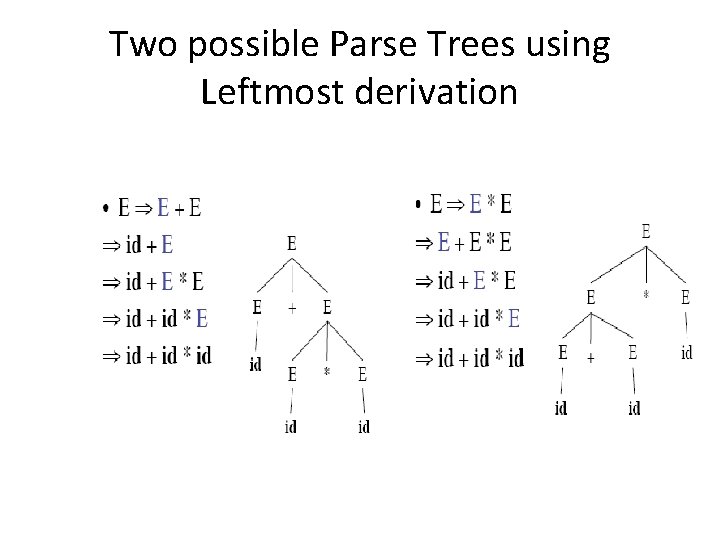
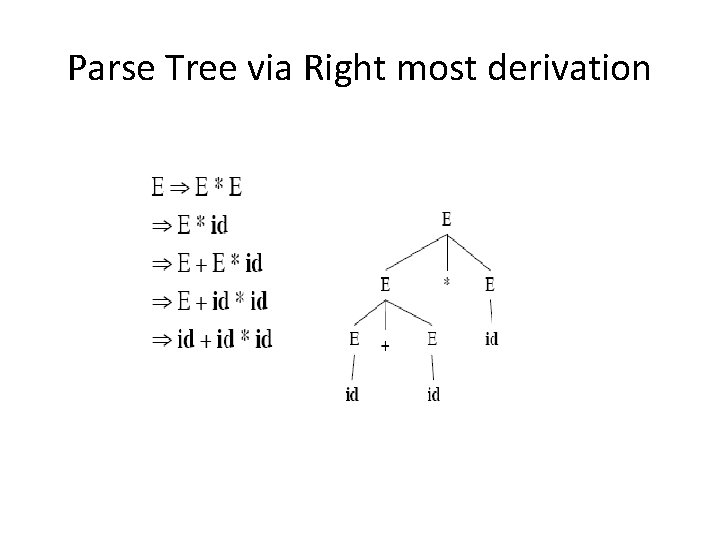
Example of Parse Tree • Suppose we have the following grammar E→E+E E→E*E E→(E) E→-E E → id Perform Left most derivation, right most derivation and construct a parse tree for the string id+id*id

Two possible Parse Trees using Leftmost derivation

Parse Tree via Right most derivation

Ambiguity • Grammar is ambiguous if more than one parse tree is possible for some string as shown in the previous example. If there are more than one left most derivations or more than one right most derivations. • Ambiguity is not acceptable – Unfortunately, it’s undecidable to check whether a given CFG is ambiguous – Some CFLs are inherently ambiguous (do not have an unambiguous CFG)

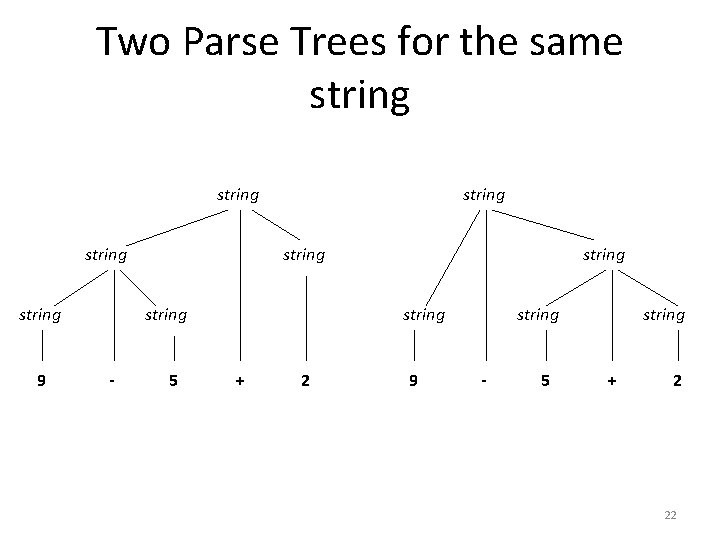
Ambiguity (cont’d) Consider the following context-free grammar: G = <{string}, {+, -, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, P, string> with production P = string + string | string - string | 0 | 1 | … | 9 This grammar is ambiguous, because more than one parse tree represents the string 9 -5+2 21

Two Parse Trees for the same string 9 string - 5 string + 2 9 string - 5 string + 2 22

Practice • Show that the following grammar is ambiguous: (Find out strings and two parse trees) 1) S AB | aa. B A a | Aa B b 3) S a. Sb | SS | ε 2) S a | ab. Sb |a. Ab A b. S | a. AAb

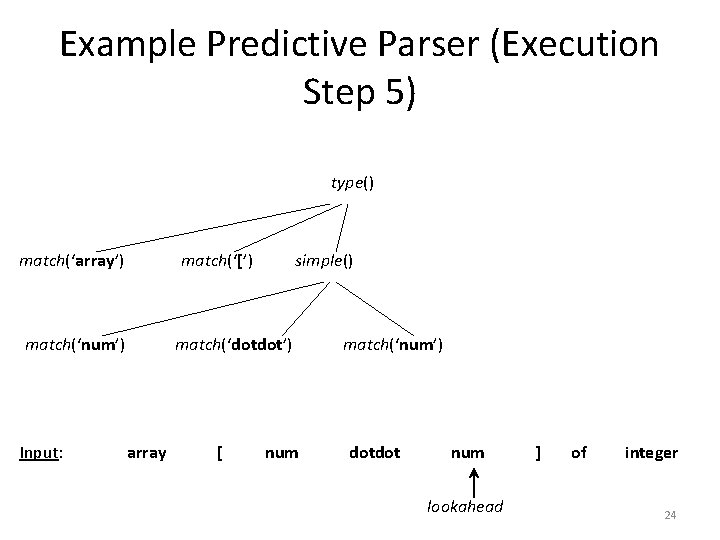
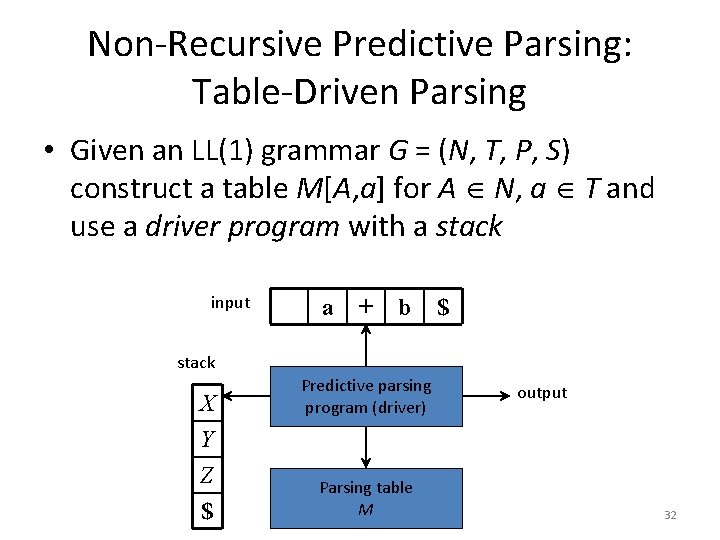
Example Predictive Parser (Execution Step 5) type() match(‘array’) match(‘[’) match(‘num’) Input: simple() match(‘dotdot’) array [ num match(‘num’) dotdot num lookahead ] of integer 24

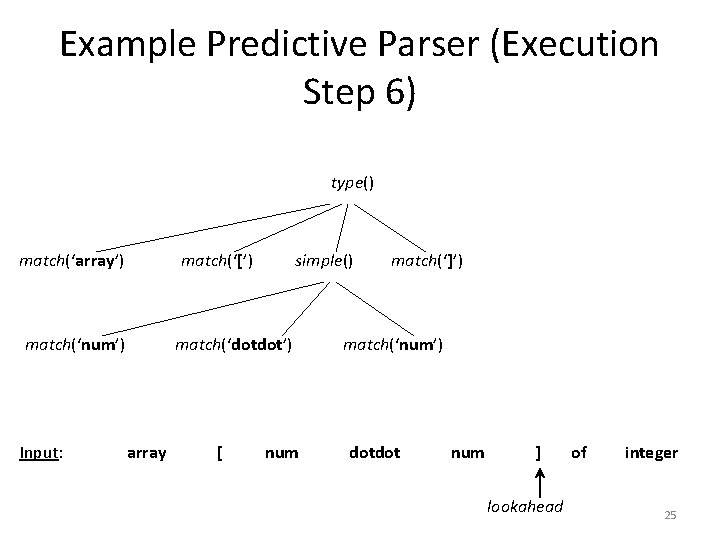
Example Predictive Parser (Execution Step 6) type() match(‘array’) match(‘[’) match(‘num’) Input: simple() match(‘dotdot’) array [ num match(‘]’) match(‘num’) dotdot num ] lookahead of integer 25

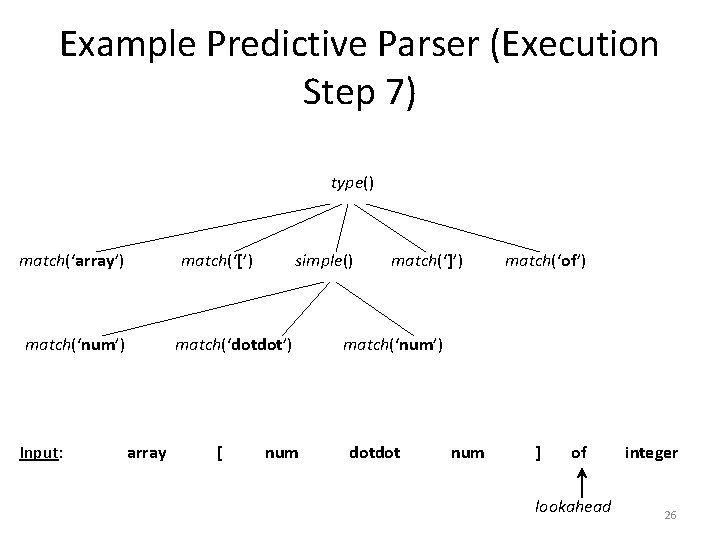
Example Predictive Parser (Execution Step 7) type() match(‘array’) match(‘[’) match(‘num’) Input: simple() match(‘dotdot’) array [ num match(‘]’) match(‘of’) match(‘num’) dotdot num ] of lookahead integer 26

Example Predictive Parser (Execution Step 8) type() match(‘array’) match(‘[’) match(‘num’) simple() match(‘dotdot’) match(‘]’) match(‘of’) match(‘num’) type() simple() match(‘integer’) Input: array [ num dotdot num ] of integer lookahead 27

FIRST( ) is the set of terminals that appear as the first symbols of one or more strings generated from type simple | ^ id | array [ simple ] of type simple integer | char | num dotdot num FIRST(simple) = { integer, char, num } FIRST(^ id) = { ^ } FIRST(type) = { integer, char, num, ^, array } 28

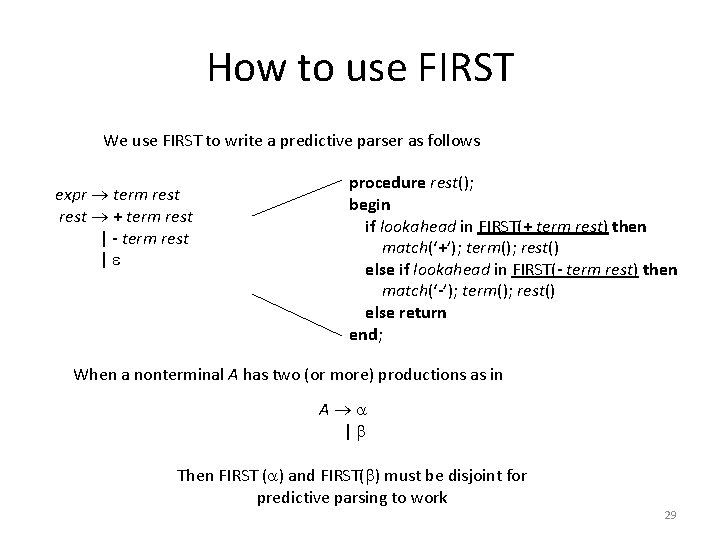
How to use FIRST We use FIRST to write a predictive parser as follows expr term rest + term rest | - term rest | procedure rest(); begin if lookahead in FIRST(+ term rest) then match(‘+’); term(); rest() else if lookahead in FIRST(- term rest) then match(‘-’); term(); rest() else return end; When a nonterminal A has two (or more) productions as in A | Then FIRST ( ) and FIRST( ) must be disjoint for predictive parsing to work 29

Predictive Parsing • • Eliminate left recursion from grammar Left factor the grammar Compute FIRST and FOLLOW Two variants: – Recursive (recursive-descent parsing) – Non-recursive (table-driven parsing) 30

Predictive Parsing Program (Driver) push($) push(S) a : = lookahead repeat X : = pop() if X is a terminal or X = $ then match(X) // moves to next token and a : = lookahead else if M[X, a] = X Y 1 Y 2…Yk then push(Yk, Yk-1, …, Y 2, Y 1) // such that Y 1 is on top … invoke actions and/or produce IR output … else error() endif until X = $ 31

Non-Recursive Predictive Parsing: Table-Driven Parsing • Given an LL(1) grammar G = (N, T, P, S) construct a table M[A, a] for A N, a T and use a driver program with a stack input a + b $ stack X Y Z $ Predictive parsing program (driver) Parsing table M output 32

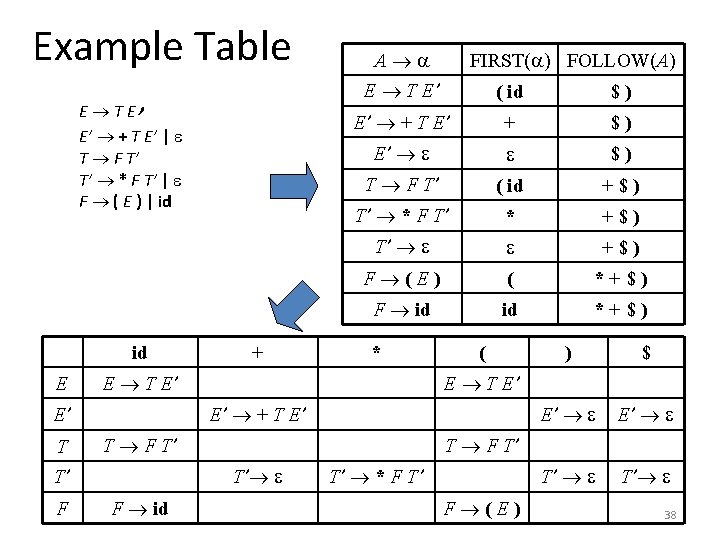
’ E TE E’ + T E’ | T F T’ T’ * F T’ | F ( E ) | id Example id+id*id id E * E T E’ ( T F T’ F push($) push(S) repeat $ E’ E’ T’ T’ T F T’ T’ T’ ) E T E’ E’ + T E’ E’ T + F id T’ * F T’ F (E) a : = lookahead X : = pop() if X is a terminal or X = $ then match(X) // moves to next token and a : = lookahead else if M[X, a] = X Y 1 Y 2…Yk then push(Yk, Yk-1, …, Y 2, Y 1) endif

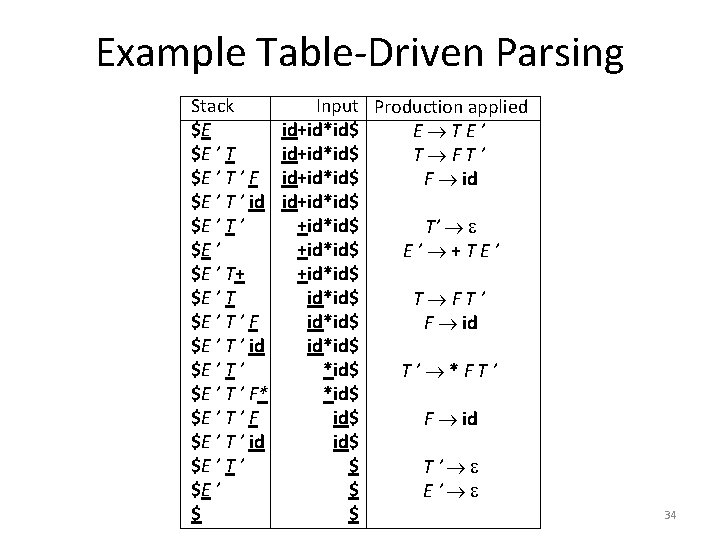
Example Table-Driven Parsing Stack $E $E ’ T ’ F $E ’ T ’ id $E ’ T ’ $E ’ T+ $E ’ T ’ F $E ’ T ’ id $E ’ T ’ F* $E ’ T ’ F $E ’ T ’ id $E ’ T ’ $E ’ $ Input Production applied id+id*id$ E TE’ id+id*id$ T FT’ id+id*id$ F id id+id*id$ T’ +id*id$ E’ +TE’ +id*id$ T FT’ id*id$ F id id*id$ T’ *FT’ *id$ F id id$ $ T ’ $ E ’ $ 34

FIRST (Revisited) • FIRST( ) = { the set of terminals that begin all strings derived from } • FIRST(a) = {a} if a T • FIRST( ) = { } • FIRST(A) = A FIRST( ) for A P • FIRST(X 1 X 2…Xk) = if for all j = 1, …, i-1 : FIRST(Xj) then add non- in FIRST(Xi) to FIRST(X 1 X 2…Xk) if for all j = 1, …, k : FIRST(Xj) then add to FIRST(X 1 X 2…Xk) 35

FOLLOW • FOLLOW(A) = { the set of terminals that can immediately follow nonterminal A } FOLLOW(A) = • for all (B A ) P do add FIRST( ){ } to FOLLOW(A) • for all (B A ) P and FIRST( ) do add FOLLOW(B) to FOLLOW(A) • for all (B A) P do add FOLLOW(B) to FOLLOW(A) • if A is the start symbol S then add $ to FOLLOW(A) 36

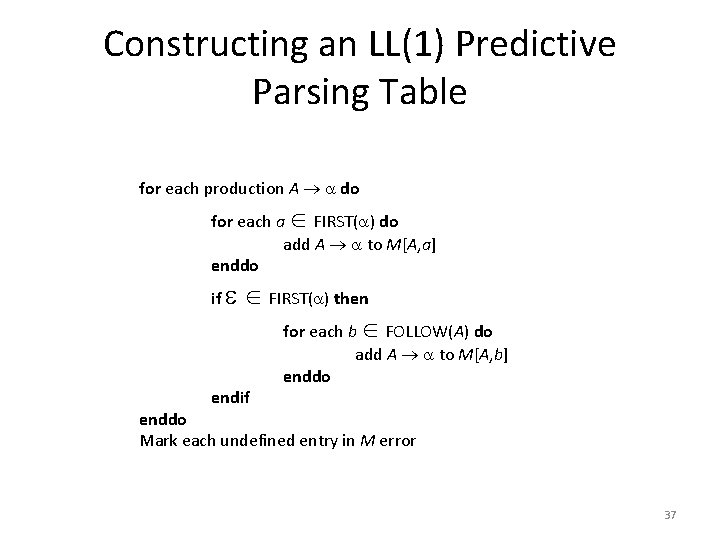
Constructing an LL(1) Predictive Parsing Table for each production A do for each a FIRST( ) do add A to M[A, a] enddo if FIRST( ) then for each b FOLLOW(A) do endif enddo add A to M[A, b] enddo Mark each undefined entry in M error 37

LL(1) Grammar • A grammar G is LL(1) if it is not left recursive and for each collection of productions A 1 | 2 | … | n for nonterminal A the following holds: 1. FIRST( i) FIRST( j) = for all i j 2. if i * then 2. a. j * for all i j 2. b. FIRST( j) FOLLOW(A) = for all i j 39

Non-LL(1) Examples Grammar S Sa|a S a. S|a S a. R| R S| Not LL(1) because: Left recursive FIRST(a S) FIRST(a) S a. Ra R S| For R: FIRST(S) FOLLOW(R) For R: S * and * 40

Recursive-Descent Parsing (Recap) • Grammar must be LL(1) • Every nonterminal has one (recursive) procedure responsible for parsing the nonterminal’s syntactic category of input tokens • When a nonterminal has multiple productions, each production is implemented in a branch of a selection statement based on input look-ahead information 41

LL(1) Grammars are Unambiguous Ambiguous grammar S i E t S SR | a SR e S | E b A S i E t S SR i e$ S a a e$ SR e S e e$ SR e$ E b b t Error: duplicate table entry a S b e S a i t $ S i E t S SR SR SR e S SR E FIRST( ) FOLLOW(A) E b SR 42

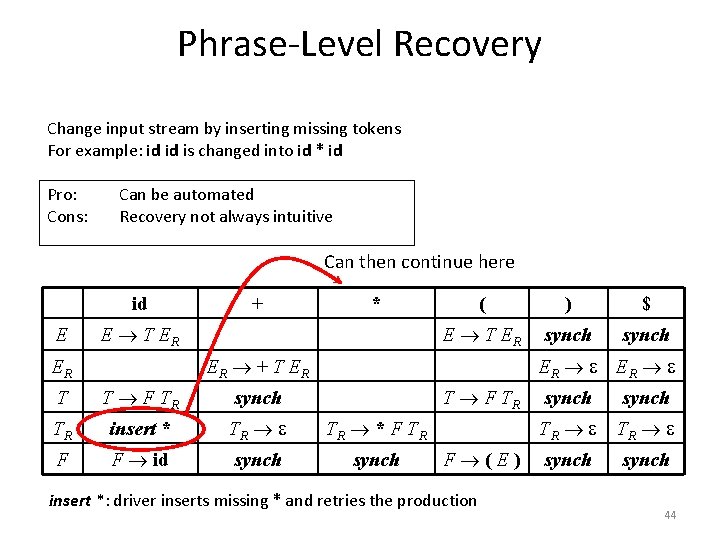
Panic Mode Recovery Add synchronizing actions to undefined entries based on FOLLOW Pro: Cons: Can be automated Error messages are needed id E synch: * ( ) $ E T ER synch ER + T ER T F TR TR F + E T ER ER T FOLLOW(E) = { ) $ } FOLLOW(ER) = { ) $ } FOLLOW(T) = { + ) $ } FOLLOW(TR) = { + ) $ } FOLLOW(F) = { + * ) $ } F id ER ER T F TR synch TR TR * F TR synch TR TR F (E) the driver pops current nonterminal A and skips input till synch token or skips input until one of FIRST(A) is found synch 43

Phrase-Level Recovery Change input stream by inserting missing tokens For example: id id is changed into id * id Pro: Cons: Can be automated Recovery not always intuitive Can then continue here id E + * E T ER ( ) $ E T ER synch ER + T ER ER T T F TR synch T F TR TR insert * TR TR * F TR F F id synch TR TR F (E) insert *: driver inserts missing * and retries the production synch 44

Error Productions Add “error production”: TR F T R to ignore missing *, e. g. : id id E T ER ER + T ER | T F TR TR * F TR | F ( E ) | id id E Pro: Cons: + Powerful recovery method Cannot be automated * E T ER ( ) $ E T ER synch ER + T ER ER T T F TR synch T F TR TR TR F T R TR TR * F TR F F id synch TR TR F (E) synch 45

Bottom-Up Parsing • LR methods (Left-to-right, Rightmost derivation) – SLR, Canonical LR, LALR • Other special cases: – Shift-reduce parsing – Operator-precedence parsing 46

Operator-Precedence Parsing • Special case of shift-reduce parsing • We will not further discuss (you can skip textbook section 4. 6) • We will not further discuss SLR, Canonical LR, LALR 47

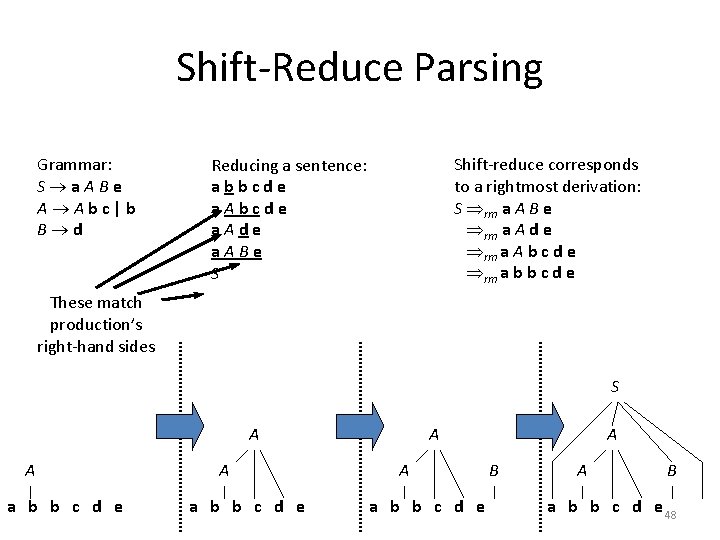
Shift-Reduce Parsing Grammar: S a. ABe A Abc|b B d Shift-reduce corresponds to a rightmost derivation: S rm a A B e rm a A d e rm a A b c d e rm a b b c d e Reducing a sentence: abbcde a. Ade a. ABe S These match production’s right-hand sides S A A a b b c d e A B a b b c d e 48

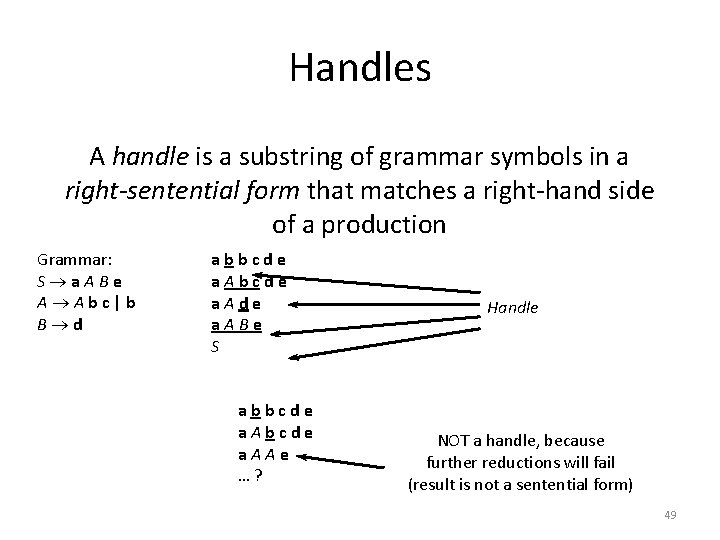
Handles A handle is a substring of grammar symbols in a right-sentential form that matches a right-hand side of a production Grammar: S a. ABe A Abc|b B d abbcde a. Ade a. ABe S abbcde a. AAe …? Handle NOT a handle, because further reductions will fail (result is not a sentential form) 49

Stack Implementation of Shift-Reduce Parsing Grammar: E E+E E E*E E (E) E id Find handles to reduce Stack $ $id $E $E+id $E+E*id $E+E*E $E+E $E Input id+id*id$ *id$ id$ $ $ Action shift reduce E id shift (or reduce? ) shift reduce E id reduce E E * E reduce E E + E accept How to resolve conflicts? 50

Conflicts • Shift-reduce and reduce-reduce conflicts are caused by – The limitations of the LR parsing method (even when the grammar is unambiguous) – Ambiguity of the grammar 51

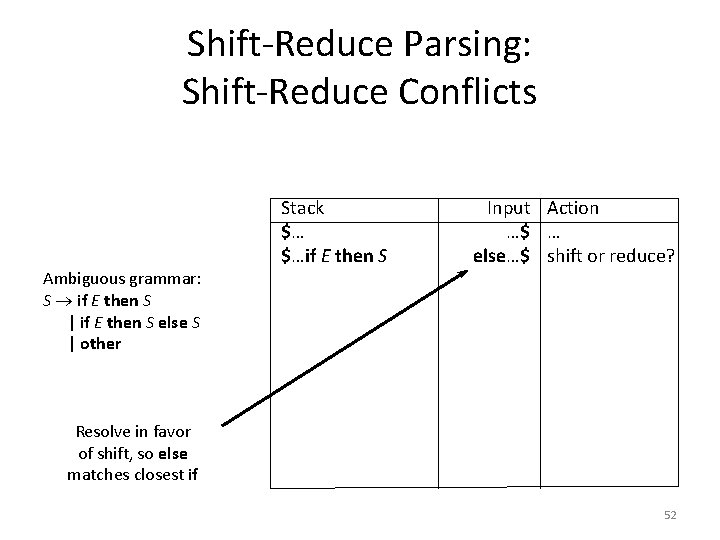
Shift-Reduce Parsing: Shift-Reduce Conflicts Ambiguous grammar: S if E then S | if E then S else S | other Stack $… $…if E then S Input Action …$ … else…$ shift or reduce? Resolve in favor of shift, so else matches closest if 52

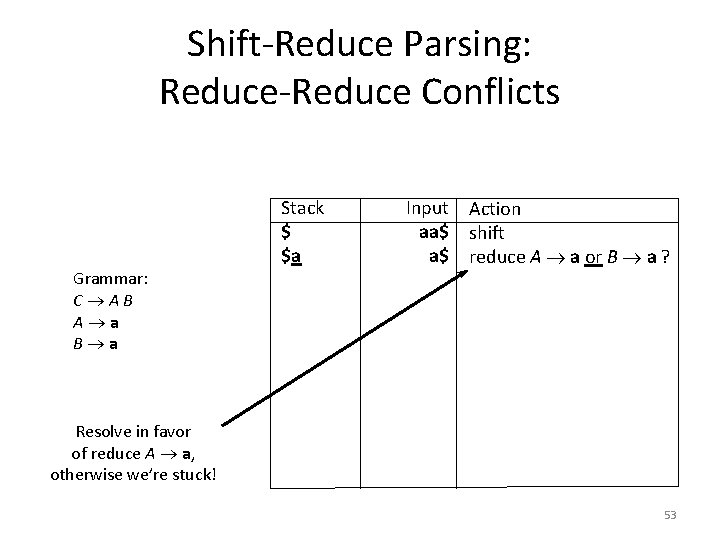
Shift-Reduce Parsing: Reduce-Reduce Conflicts Grammar: C AB A a B a Stack $ $a Input aa$ a$ Action shift reduce A a or B a ? Resolve in favor of reduce A a, otherwise we’re stuck! 53

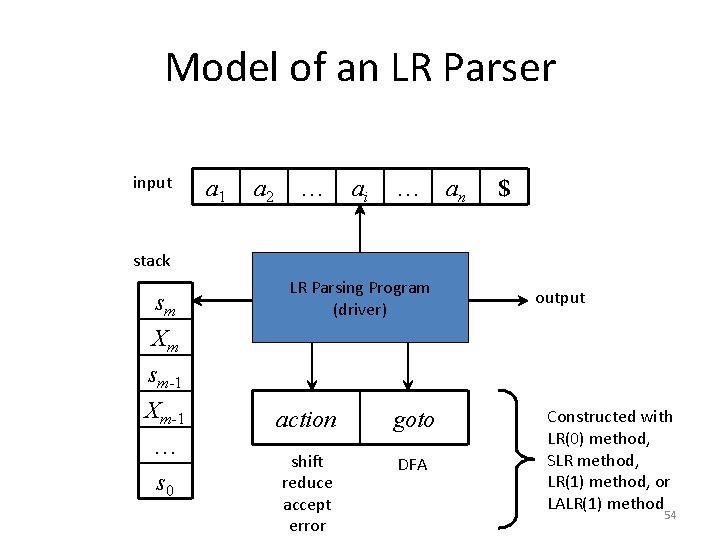
Model of an LR Parser input a 1 a 2 … ai … an $ stack sm Xm sm-1 Xm-1 … s 0 LR Parsing Program (driver) action goto shift reduce accept error DFA output Constructed with LR(0) method, SLR method, LR(1) method, or LALR(1) method 54

LR Parsing (Driver) Configuration ( = LR parser state): (s 0 X 1 s 1 X 2 s 2 … Xm sm, ai ai+1 … an $) stack input If action[sm, ai] = shift s then push ai, push s, and advance input: (s 0 X 1 s 1 X 2 s 2 … Xm sm ai s, ai+1 … an $) If action[sm, ai] = reduce A and goto[sm-r, A] = s with r=| | then pop 2 r symbols, push A, and push s: (s 0 X 1 s 1 X 2 s 2 … Xm-r sm-r A s, ai ai+1 … an $) If action[sm, ai] = accept then stop If action[sm, ai] = error then attempt recovery 55

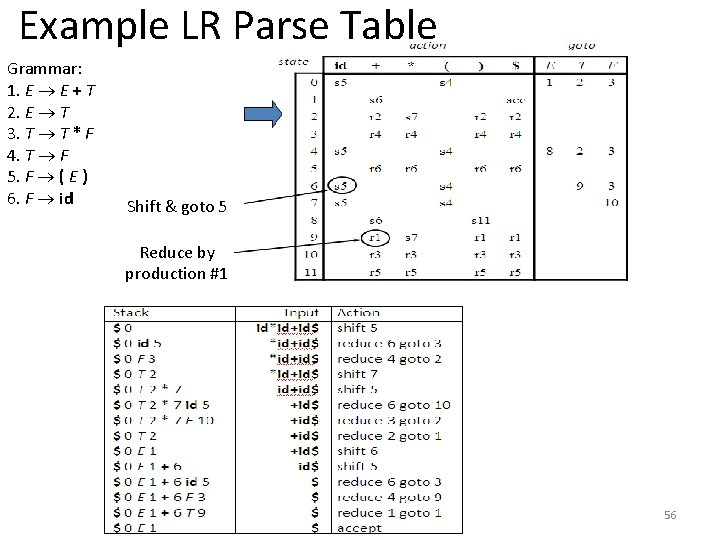
Example LR Parse Table Grammar: 1. E E + T 2. E T 3. T T * F 4. T F 5. F ( E ) 6. F id Shift & goto 5 Reduce by production #1 56

LL(k) and LR(k) • LL(k) parse tables computed using FIRST/FOLLOW • LR(k) parsing tables computed using closure/goto • For a grammar to be LR (k) we must be able to recognize the occurrence of right hand side of the production having seen k input lookaheads 57