Lecture 8 Basic Images Manipulation 2 1 Contents

Lecture 8: Basic Images Manipulation (2) 1

Contents Displaying image in Java Printing Manipulation of pixel data 2

Displaying Image in Java Image display using awt. Image display using swing components. 3

Printing How do we simulate intermediate shades of grey in an 8 -bit image? How can we use small number of coloured inks to simulate the huge range of colours possible in a 24 -bit image? 4

Printing Grayscale Images Problem: How to print a gray-scale image when the only color ink available is black (the ink) and white (the paper)? Í This is the problem faced by newspapers and any other print media. Í Newspapers print at 80 -100 DPI (dots per inch) Í Magazines print at 200 -300 DPI Í Color printing is a more complicated variant of this problem. Í The solution is to use a technique known as halftoning. ÍThe process of generating binary pattern of black and white dots from an image. 5

Halftoning Photographs are images with continuous shades of black, white, and gray. These shades are tones. Halftoning is a technique, originally developed for the printing industry, to reproduce continuous tone images using printing techniques capable of black and white only, not shades of gray. 6

Introduction Need for Digital Image Halftoning Examples of reduced grayscale/color resolution Laser and inkjet printers ($9. 3 B revenue in 2001 in US) Facsimile machines Low-cost liquid crystal displays Halftoning is wordlength reduction for images Grayscale: 8 -bit to 1 -bit (binary) Color displays: 24 -bit RGB to 12 -bit RGB (e. g. PDA/cell) Color displays: 24 -bit RGB to 8 -bit RGB (e. g. cell phones) Color printers: 24 -bit RGB to CMY (each color binarized) Halftoning tries to reproduce full range of gray/ color while preserving quality & spatial resolution. 7

Halftoning The process of transforming a grayscale image to a halftone. Create the illusion of gray-scale by varying the average dot density in local regions of the image Dots are always something that can be counted and it must be possible to hold a measuring stick to them. Takes advantage of the fact that the eye integrates intensity of small image regions. Sacrifices spatial resolution for gray-scale resolution (unless the output device can be over-sampled as most ink-jet printers are these days) Spatial refers to image itself, based on direct manipulation pixels. 8

Halftoning Consider a grayscale image (left) which is halftoned (right) for printing. The right image looks like a grayscale image but is actually only black and white! Zooming in on the image reveals “pixel” sizes of differing sizes and shapes. 9 Source: www. adobe. com

Halftoning 10

Digital Halftoning The previous example is from the domain of print media which uses physical filters, lights, and film to generate the halftoned images. Digital halftoning cannot be done this way since digital images consist of identically shaped pixels (usually rectangular) which are either black or white. The main problem is “Should this pixel be white or black”? Several solutions to this problem exist • Bi-level Thresholding • Font/Pattern replacement • Random thresholding • Dither matrices • Error Diffusion 11

Bilevel Thresholding Re-quantize the image using a 1 bit color If the gray-level of a pixel is less than some threshold value then set the output to black otherwise set the output to white. The threshold value may be the “center of the available gray-scale range” The threshold value may by the “average of all pixels in the image” The T value can be choosen e. g inspecting the histogram image f. or 12

Bi-level Thresholding Example Original Image Absolute Threshold Adaptive Threshold 13

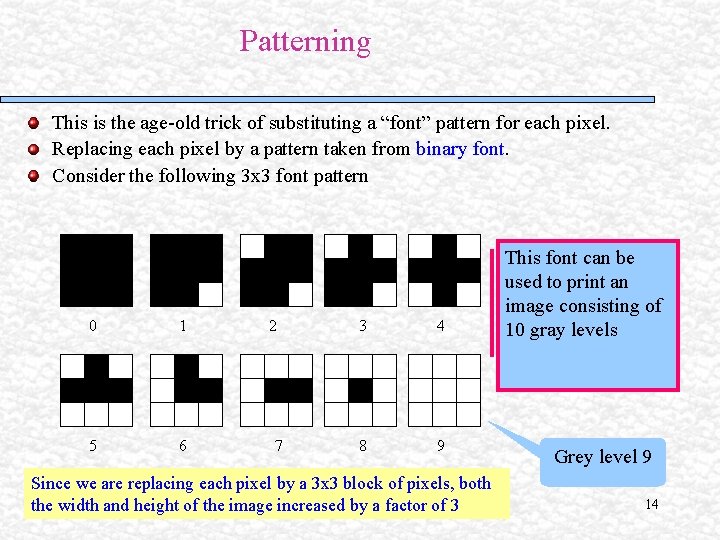
Patterning This is the age-old trick of substituting a “font” pattern for each pixel. Replacing each pixel by a pattern taken from binary font. Consider the following 3 x 3 font pattern 0 1 5 6 2 7 3 4 8 9 Since we are replacing each pixel by a 3 x 3 block of pixels, both the width and height of the image increased by a factor of 3 This font can be used to print an image consisting of 10 gray levels Grey level 9 14

Patterning 15

Patterning algorithm pattern. Halftone(im, font) INPUT: Grayscale image im and a set of font patterns OUTPUT: BW halftone of the input Let output be an “empty” image for every pixel P in im let F be the font that most closely approximates the actual gray-level of P replace pixel P with font F in the output image return output Given an Nx. N font there are N 2+1 “gray levels” to choose from. N < number of grayscale level. The output image is N times larger (in both dimensions) than the original. Font patterns must be chosen carefully to avoid the introduction of artificial patterns into the output. Drawback – create false lines and contours in homogeneous image regions. 16

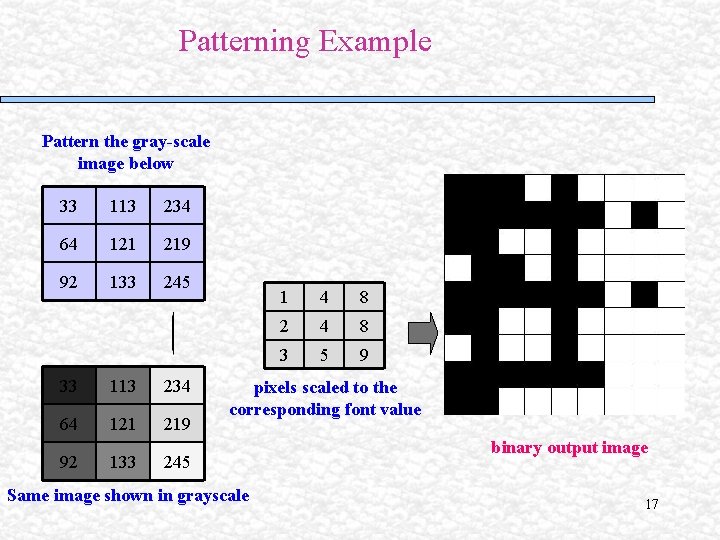
Patterning Example Pattern the gray-scale image below 33 113 234 64 121 219 92 133 245 1 4 8 2 4 8 3 5 9 pixels scaled to the corresponding font value Same image shown in grayscale binary output image 17

Patterning Example 18

Random Thresholding Selects a threshold value at random for every pixel. The output is white if the pixel value exceeds the threshold and black otherwise. High intensity pixels have a greater chance of becoming white while low intensity pixels have a greater change of becoming black Attempts to spread the error per pixel evenly (or randomly) throughout the image algorithm random. Dither(image) INPUT: An image OUTPUT: A B/W dithered version of the input Let output be an “empty” image for every pixel P of the input let T be a random value between 0 and 255 if P <= T then output black else output white return output 19

Random Dithering Example 20

Dither Matrices Selects a threshold value using a pre-determined pattern. The output is white if the pixel value exceeds the pre-determined threshold and black otherwise. The matrix is laid like a tile over entire image and each pixel value is compared with the corresponding threshold from the matrix. Attempts to spread the error per pixel evenly throughout small regions of the image (and hence, throughout the entire image). algorithm matrix. Dither(image, M) INPUT: An image and an Nx. N “dither” matrix M OUTPUT: A B/W dithered version of the input Let output be an “empty” image for every pixel P(x, y)of the input let T be M[x%N][y%N] if P <= T then output black else output white return output 21

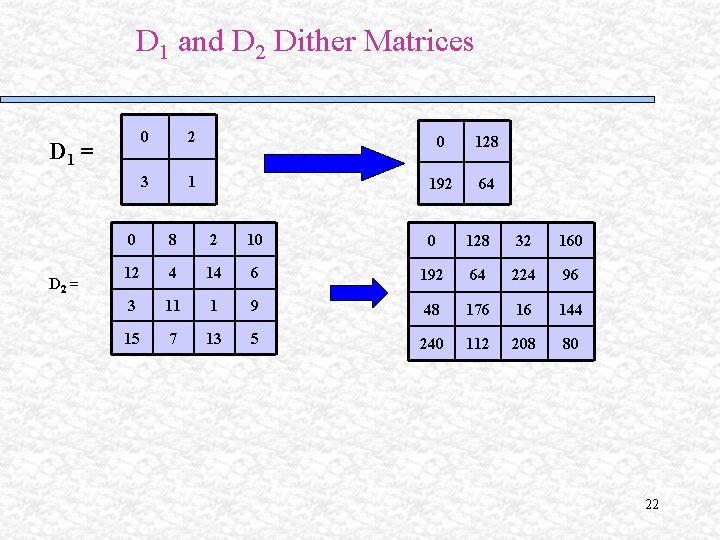
D 1 and D 2 Dither Matrices D 1 = D 2 = 0 2 0 128 3 1 192 64 0 8 2 10 0 128 32 160 12 4 14 6 192 64 224 96 3 11 1 9 48 176 16 144 15 7 13 5 240 112 208 80 22

2 x 2 Pattern Dithering Example 23

4 x 4 Pattern Dithering Example 24

25

Halftoning: Floyd-Steinberg error diffusion Typical threshold value is 128 for images with pixel values in [0, 255] To correct the errors introduced by thresholding. Selects a threshold value which is at the center of the gray-scale range The output is white if the pixel value exceeds the threshold and black otherwise. The error of a pixel is the difference between the actual value of the pixel and the value selected (black or white) This error is carried over to nearby pixels in a systematic way This gives an average density of white dots proportional to the average intensity level within a region of the image 3/16 Pixel 7/16 5/16 1/16 26

Floyd-Steinberg Pseudocode 27

Floyd-Steinberg 28

Floyd-Steinberg Java implementation of Algorithm 5. 1 29

Floyd-Steinberg 30

Floyd-Steinberg Returns the smaller of two int values. That is, the result the argument closer to the value of Integer. MIN_VALUE. If the arguments have the same value, the result is that same value. 31

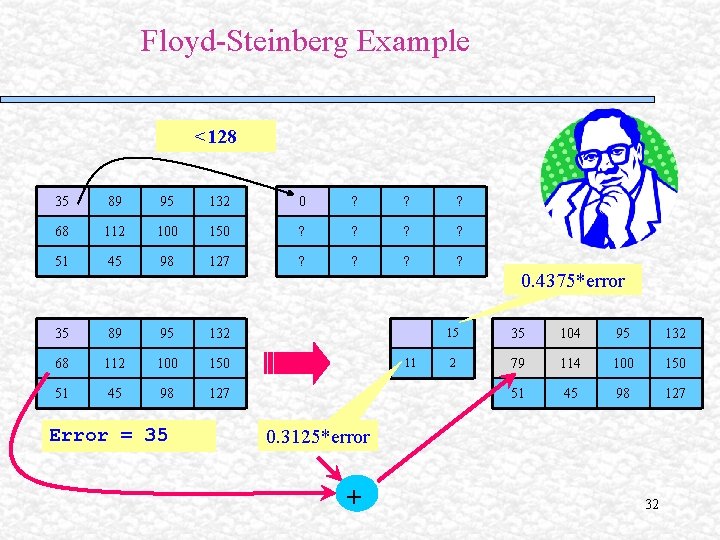
Floyd-Steinberg Example <128 35 89 95 132 0 ? ? ? 68 112 100 150 ? ? 51 45 98 127 ? ? 35 89 95 132 68 112 100 150 51 45 98 127 Error = 35 11 0. 4375*error 15 35 104 95 132 2 79 114 100 150 51 45 98 127 0. 3125*error + 32

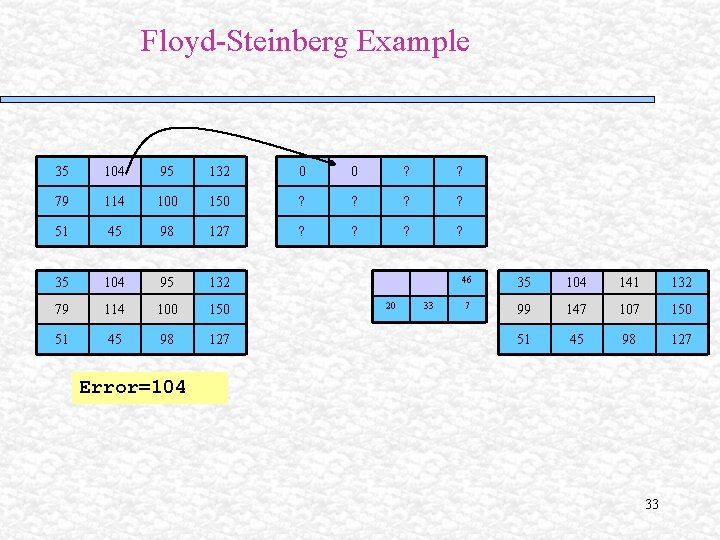
Floyd-Steinberg Example 35 104 95 132 0 0 ? ? 79 114 100 150 ? ? 51 45 98 127 ? ? 35 104 95 132 79 114 100 150 51 45 98 127 20 33 46 35 104 141 132 7 99 147 107 150 51 45 98 127 Error=104 33

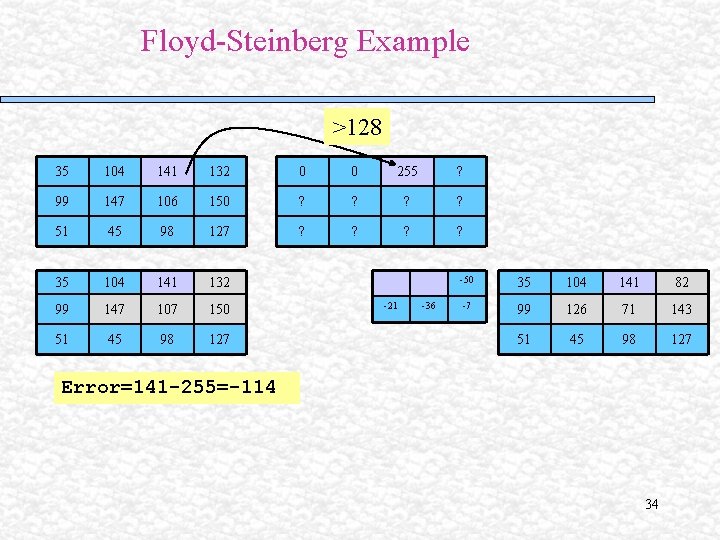
Floyd-Steinberg Example >128 35 104 141 132 0 0 255 ? 99 147 106 150 ? ? 51 45 98 127 ? ? 35 104 141 132 99 147 107 150 51 45 98 127 -21 -36 -50 35 104 141 82 -7 99 126 71 143 51 45 98 127 Error=141 -255=-114 34

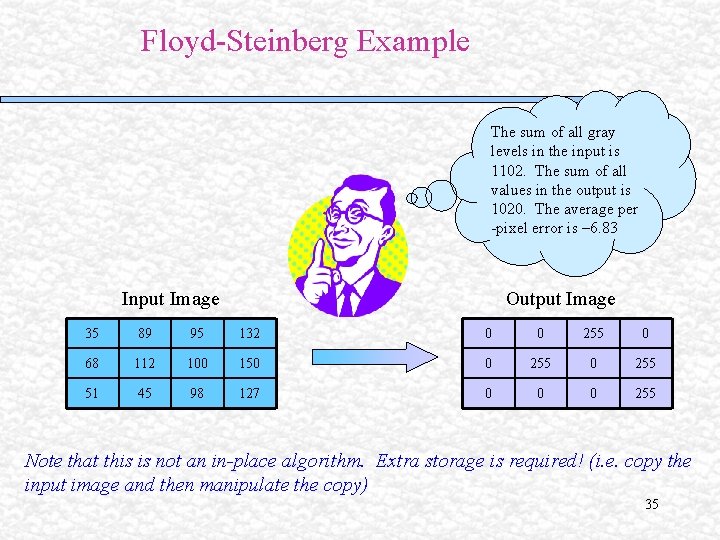
Floyd-Steinberg Example The sum of all gray levels in the input is 1102. The sum of all values in the output is 1020. The average per -pixel error is – 6. 83 Input Image Output Image 35 89 95 132 0 0 255 0 68 112 100 150 0 255 51 45 98 127 0 0 0 255 Note that this is not an in-place algorithm. Extra storage is required! (i. e. copy the input image and then manipulate the copy) 35

Floyd-Steinberg Error Diffusion 36

Colour Printing 37

Colour Printing (Great 1 Page tutorial from Adobe) Color prints are typically constructed from 4 half-toned images using the CMYK color model (K is black). The individual planes are halftoned using rotated screens to avoid odd-patterned moire effects. The screen angles are typically Y=0° C=15° M=75° K=45° Source: www. adobe. com 38

Colour Printing (Great 1 Page tutorial from Adobe) When viewed with the naked eye at normal viewing distance (inset), the image appears to have continuous color tone. When viewed closely, the superimposed cyan, magenta, yellow, and black halftones become apparent. Source: www. adobe. com 39

Colour Half-toning A common problem arises when displaying images on systems with limited resources. Imagine a web browser loading a 24 -bit image. The web browser is using an 5 -bit display with a pre-configured color palette. How can the image be displayed? Color dithering is used to display high-color images using a limited palette of colors. The usual algorithm is a modification of Floyd-Steinberg diffusion. interlaced pixels 40

Colour Dithering 41

Colour Halftoning 42

Colour Halftoning So What's Really Important? The choice of color reduction function and options depends upon the requirements for speed of execution, image quality, and ability to display multiple images at the same time. Hints For fastest speed use a standard palette. For highest image quality use diffusion scatter. To display multiple images simultaneously use the same palette for all images. 43

Colour Dithering 44

Colour Dithering When do we need dithering? Under fixed lighting conditions the typical person can discern approximately 100 different brightness levels. This number varies slightly with hue (for instance we can see more distinct shades of green than blue). Which particular set of 100 levels also changes as a function of the ambient lighting conditions. The 256 colors available for each primary in a true color display are usually adequate for representing these 100 levels under normal indoor lighting (when the nonlinearities of the display are properly compensated for). Thus, there is usually no need to dither a true color display. On index displays dithering is frequently used to represent color images. Given a 256 entry color map you can only represent approximately 6 colors per red, green, and blue primary (6 x 6 x 6=216). However, if just one or two hues are used it is possible to allocate enough color table entries (~50 per hue) so that dithering can be avoided. 45

Color Dithering 46

Color Dithering Problems with dithering When a signal, or color, is modified from it original value by the addition of some other value, it is said that noise has been added White noise generates values within some interval such that all values are equally likely. Solution generate symmetric values. 47

Color Dithering To find the error between two RGB colors, compute the length of the 3 D vector between the colors. algorithm color. Dither(Image IM, Palette CP) for every pixel P in IM (left-to-right-top-to-bottom) set the color of P to the nearest matching color in CP diffuse the error using floyd-steinberg on each band 48

Color Dithering 49

Manipulation of Pixel Data Extracting regions of interest. Basic geometric manipulation. 50

Extracting Region of Interest A region of interest (ROI) is a rectangular area within the image defined either by: The coordinates of the pixels at its upper-left & lower-right corners or The coordinates of the pixels at its upper-left corner & its dimensions. Commonly use to limit the extent of image processing operations to some small part of the image. Interactive image processing software will often provide facility to define ROIs of images using mouse etc. 51

Extracting Region of Interest Java’s Buffered. Image class has 3 methods that useful when operating on ROIs: Raster get. Data(Rectangle rect) Void set. Data(Raster raster) Buffered. Image get. Subimage(int x, int y, int w, int h). Example of ROI application: Mean. ROI application, which displays an image, allow the user to draw a ROI on it and then computes mean grey level within that ROI (see course web page). 52

Extracting Region of Interest The get. Data() method takes as its sole parameter a Rectangle object that specifies the position and dimensions of the ROI. It returns the data from that ROI as a Raster object. The data stored within the raster are independent of the image on which get. Data() was called, so subsequent changes to the image will not affect the raster. However, the raster’s coordinate system is that of the original image. This means that the first pixel in the raster has the same coordinates as the ROI’s origin. We must be carefhl to take this into account when processing raster data. Instances of Raster are read-only, but we may cast the object returned by get. Data() to a Writable. Raster if we wish to modify the pixel values. The modified raster can then be loaded back into its parent image by invoking the set. Data() method of the image, with the raster as a parameter. If in-place processing of a ROI is required, the get. Subimage() method of Buffered. Image may be more convenient. Given the coordinates and dimensions of the ROl as parameters, this method returns a subimage that shares the same data array as the parent image. This means that changes made to pixel values in the subimage will affect the parent image. The coordinate system of the subimage is not that of the parent image, so its pixels are indexed starting from (0, 0). An example of ROl usage can be seen in Listing 5. 13. This shows two versions of a method mean. Value(). The first computes the mean pixel value in the supplied image (assumed to be greyscale). The second computes the mean within a ROI specified by a Rectangle object. Note that there is no need to duplicate any code in the second version of the method; all that we need to do is invoke get. Subimage() on the image using the ROI parameters contained in the Rectangle object and then pass the image that is returned to the first version of mean. Value(). Both of these methods are used in the Mean. ROI application described earlier. 53

Extracting Region of Interest 54

Basic Geometric Manipulation Enlargement or shrinking. Accomplished by replicating or skipping pixels. Used to magnify small details in an image , or reduce a large image in size. For a pixel (x, y) in the output image (enlarge by factor n), the corresponding pixel in the input image is at (x/n, y/n). To shrink an image by n factor, we must sample every nth pixel in the horizontal and vertical dimension and ignore the others. 55

Basic Geometric Manipulation Rotation. Relatively simple to implement for the special case where the angle is a multiple of 900. Reflection along the x or y axis. Reflection along either of the image axes is simply involves reversing the ordering of pixels in the rows or columns of the image. 56

57

58

59

Assignment 2 (20%) Write a Java program that can: Read and display an image file. Perform the following digital halftoning and display the halftone images: • Random Thresholding • Floyd-Steinberg error diffusion Allow the user to select a region of interest (ROI) and then: • Extract the ROI from the image and display the enlarged (by a factor of n) image. Allow the user to select the reflection line and display the output. You can work in a group (maximum of 3 students in a group). 60

Thank you Q&A 61