Lecture 7 Tree and Array Multipliers Required Reading

















- Slides: 36

Lecture 7 Tree and Array Multipliers

Required Reading Behrooz Parhami, Computer Arithmetic: Algorithms and Hardware Design Chapter 11, Tree and Array Multipliers Chapter 12. 5, The special case of squaring Note errata at: http: //www. ece. ucsb. edu/~parhami/text_comp_arit_1 ed. htm#errors


Notation a Multiplicand ak-1 ak-2. . . a 1 a 0 x Multiplier xk-1 xk-2. . . x 1 x 0 p Product (a x) p 2 k-1 p 2 k-2. . . p 2 p 1 p 0

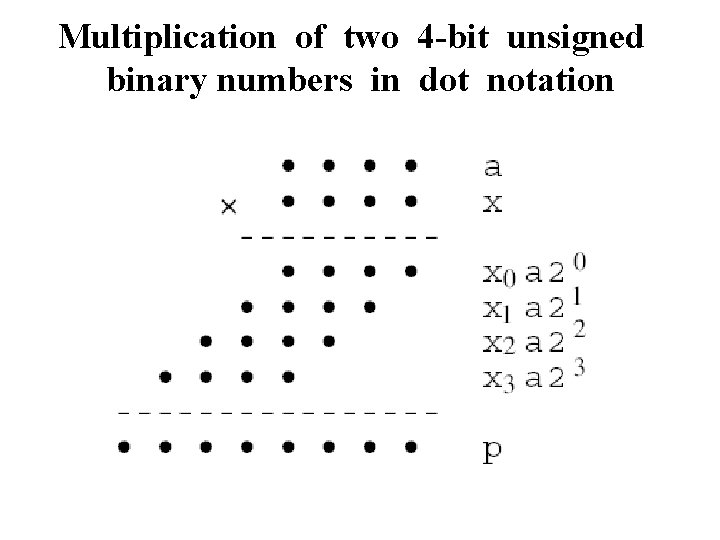
Multiplication of two 4 -bit unsigned binary numbers in dot notation

Basic Multiplication Equations k-1 p=a x x = xi 2 i i=0 k-1 p = a x = a xi 2 i = i=0 = x 0 a 20 + x 1 a 21 + x 2 a 22 + … + xk-1 a 2 k-1

Unsigned Multiplication x ax 0 20 a 4 a 3 a 2 a 1 a 0 x 4 x 3 x 2 x 1 x 0 a 4 x 0 a 3 x 0 a 2 x 0 a 1 x 0 a 0 x 0 ax 1 21 a 4 x 1 a 3 x 1 a 2 x 1 a 1 x 1 a 0 x 1 + ax 2 22 a 4 x 2 a 3 x 2 a 2 x 2 a 1 x 2 a 0 x 2 ax 3 23 a 4 x 3 a 3 x 3 a 2 x 3 a 1 x 3 a 0 x 3 ax 4 24 a 4 x 4 a 3 x 4 a 2 x 4 a 1 x 4 a 0 x 4 p 9 p 8 p 7 p 6 p 5 p 4 p 3 p 2 p 1 p 0

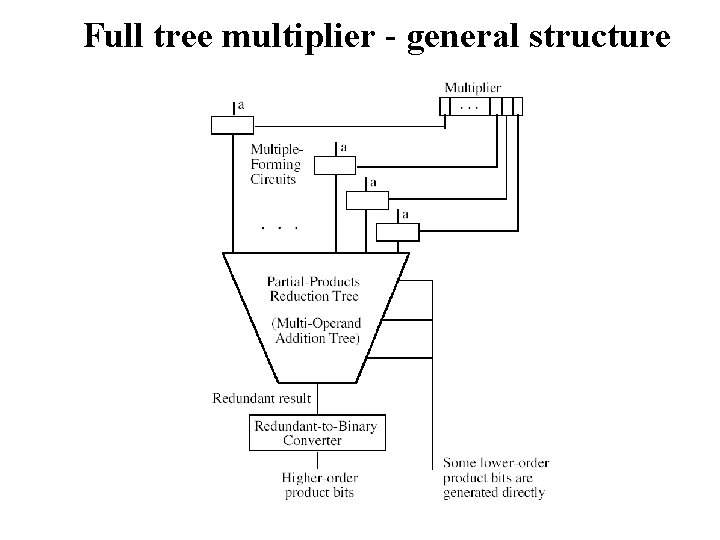
Full tree multiplier - general structure

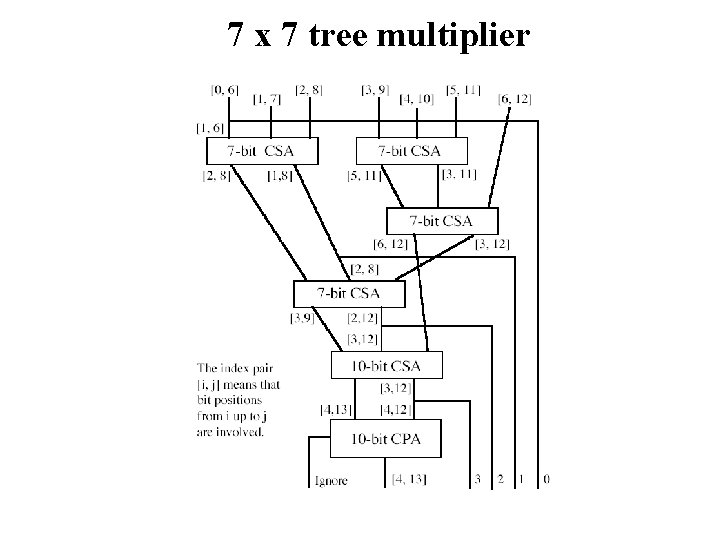
7 x 7 tree multiplier

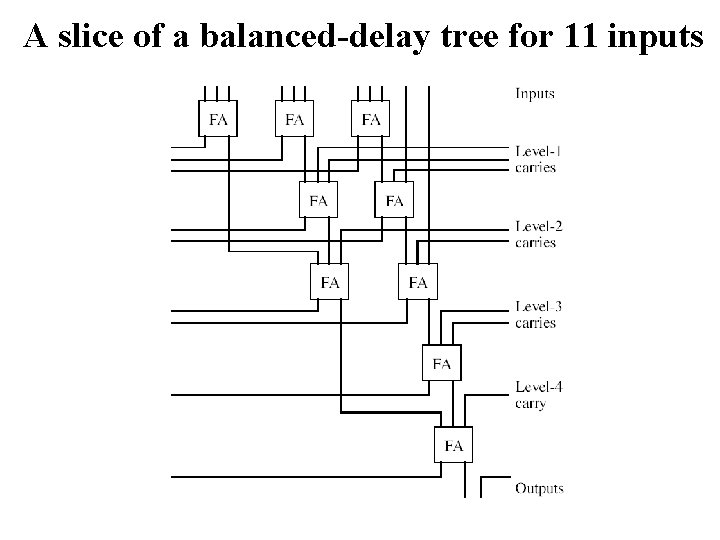
A slice of a balanced-delay tree for 11 inputs

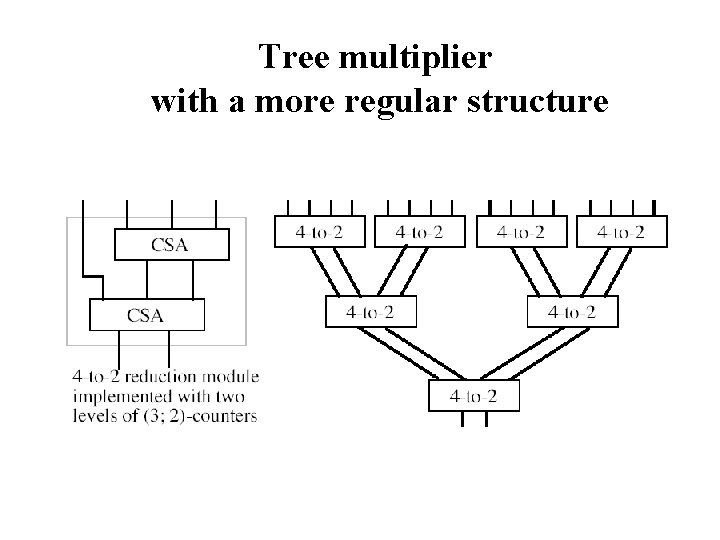
Tree multiplier with a more regular structure

Unsigned vs. Signed Multiplication Unsigned Signed 1111 x 1111 15 x 15 1111 x 1111 -1 x -1 11100001 225 00000001 1 12

2’s Complement Multiplication (1) x -24 23 22 21 20 a 4 a 3 a 2 a 1 a 0 x 4 x 3 x 2 x 1 x 0 x 24 23 -a 4 a 3 -x 4 x 3 21 20 a 2 a 1 a 0 x 2 x 1 x 0 22

2’s Complement Multiplication (2) x -a 4 a 3 a 2 a 1 a 0 -x 4 x 3 x 2 x 1 x 0 -a 4 x 0 a 3 x 0 a 2 x 0 a 1 x 0 a 0 x 0 -a 4 x 1 a 3 x 1 a 2 x 1 a 1 x 1 a 0 x 1 + -a 4 x 2 a 3 x 2 a 2 x 2 a 1 x 2 a 0 x 2 -a 4 x 3 a 3 x 3 a 2 x 3 a 1 x 3 a 0 x 3 a 4 x 4 -a 3 x 4 -a 2 x 4 -a 1 x 4 -a 0 x 4 -p 9 p 8 p 7 p 6 p 5 p 4 p 3 p 2 p 1 p 0 29 28 27 26 25 24 23 22 21 20

2’s Complement Multiplication (3) -p 9 p 8 p 7 p 6 p 5 p 4 p 3 p 2 p 1 p 0 29 28 27 26 25 24 23 22 21 20 p 9 p 8 p 7 p 6 p 5 p 4 p 3 p 2 p 1 p 0 -29 28 27 26 25 24 23 22 21 20

2’s Complement Multiplication (4) z=1 -z - aj xi = - aj (1 - xi) = aj xi - aj = aj xi + aj - 2 aj - aj xi = - (1 - aj ) xi = aj xi - xi = aj xi + xi - 2 xi - aj xi = - (1 - aj xi) = aj xi - 1 = aj xi + 1 - 2 -aj = - (1 - aj) = aj - 1 = aj + 1 - 2 -xi = - (1 - xi) = xi - 1 = xi + 1 - 2

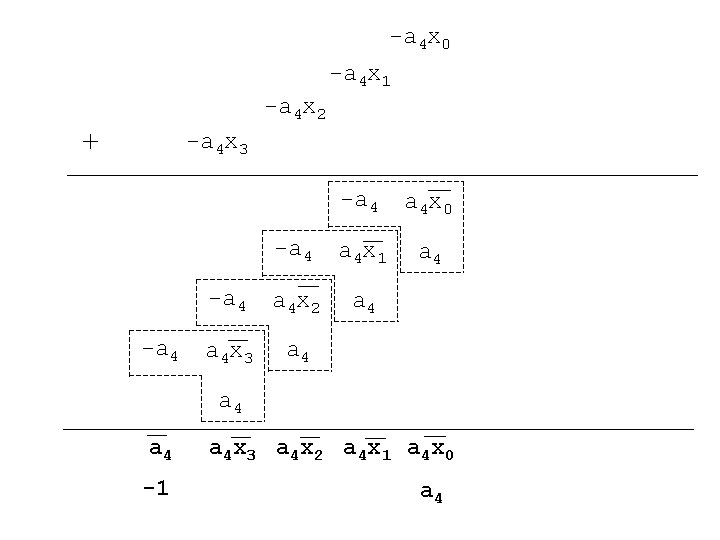
-a 4 x 0 -a 4 x 1 -a 4 x 2 + -a 4 x 3 -a 4 a 4 x 0 -a 4 a 4 x 1 a 4 -a 4 a 4 x 2 a 4 x 3 a 4 a 4 -1 a 4 x 3 a 4 x 2 a 4 x 1 a 4 x 0 a 4

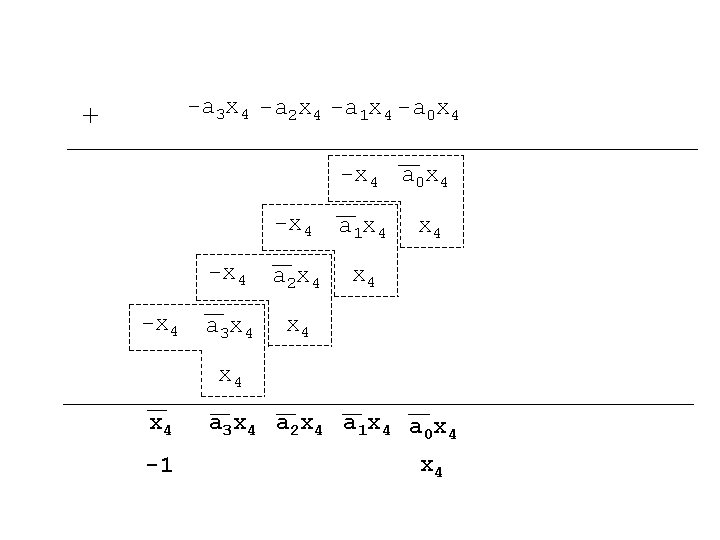
-a 3 x 4 -a 2 x 4 -a 1 x 4 -a 0 x 4 + -x 4 a 0 x 4 -x 4 a 1 x 4 -x 4 a 2 x 4 a 3 x 4 x 4 x 4 -1 a 3 x 4 a 2 x 4 a 1 x 4 a 0 x 4

29 28 27 a 4 x 3 a 4 x 2 a 4 x 1 a 4 x 0 -1 x 4 -1 -1 26 25 24 a 3 x 4 a 2 x 4 a 1 x 4 a 0 x 4 a 4 a 4 x 3 a 4 x 2 a 4 x 1 a 4 x 0 x 4 a 3 x 4 a 2 x 4 a 1 x 4 a 0 x 4 a 4 x 4 1 a 4 x 3 a 4 x 2 a 4 x 1 a 4 x 0 x 4 a 3 x 4 a 2 x 4 a 1 x 4 a 0 x 4 a 4 -29 x 4

Baugh-Wooley 2’s Complement Multiplier x -a 4 a 3 a 2 a 1 a 0 -x 4 x 3 x 2 x 1 x 0 a 4 x 0 a 3 x 0 a 2 x 0 a 1 x 0 a 0 x 0 a 4 x 1 a 3 x 1 a 2 x 1 a 1 x 1 a 0 x 1 + a 4 x 2 a 3 x 2 a 2 x 2 a 1 x 2 a 0 x 2 a 4 x 3 a 4 x 4 a 3 x 4 a 4 x 4 1 p 9 p 8 p 7 -29 28 27 a 3 x 3 a 2 x 3 a 1 x 3 a 0 x 3 a 2 x 4 a 1 x 4 a 0 x 4 a 4 x 4 p 6 p 5 p 4 p 3 p 2 p 1 p 0 26 25 24 23 22 21 20

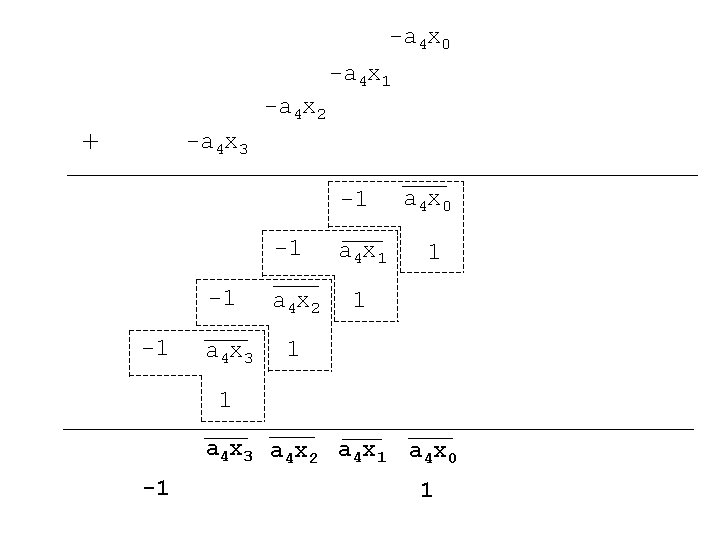
-a 4 x 0 -a 4 x 1 -a 4 x 2 + -a 4 x 3 -1 -1 a 4 x 2 a 4 x 3 1 a 4 x 0 1 1 1 a 4 x 3 a 4 x 2 a 4 x 1 a 4 x 0 -1 1

-a 3 x 4 -a 2 x 4 -a 1 x 4 -a 0 x 4 + -1 -1 a 2 x 4 a 3 x 4 1 a 1 x 4 a 0 x 4 1 1 1 a 3 x 4 a 2 x 4 a 1 x 4 a 0 x 4 -1 1

29 28 27 26 25 24 a 4 x 3 a 4 x 2 a 4 x 1 a 4 x 0 -1 1 a 3 x 4 a 2 x 4 a 1 x 4 a 0 x 4 1 -1 a 4 x 3 a 4 x 2 a 4 x 1 a 4 x 0 a 3 x 4 a 2 x 4 a 1 x 4 a 0 x 4 -1 1 a 4 x 3 a 4 x 2 a 4 x 1 a 4 x 0 a 3 x 4 a 2 x 4 a 1 x 4 a 0 x 4 1 -29 1

Modified Baugh-Wooley Multiplier x -a 4 a 3 a 2 a 1 a 0 -x 4 x 3 x 2 x 1 x 0 a 4 x 0 a 3 x 0 a 2 x 0 a 1 x 0 a 0 x 0 a 4 x 1 a 3 x 1 a 2 x 1 a 1 x 1 a 0 x 1 + a 4 x 2 a 3 x 2 a 2 x 2 a 1 x 2 a 0 x 2 a 4 x 3 a 4 x 4 a 3 x 3 a 2 x 3 a 1 x 3 a 0 x 3 a 2 x 4 a 1 x 4 a 0 x 4 1 1 p 9 p 8 p 7 p 6 p 5 p 4 p 3 p 2 p 1 p 0 -29 28 27 26 25 24 23 22 21 20

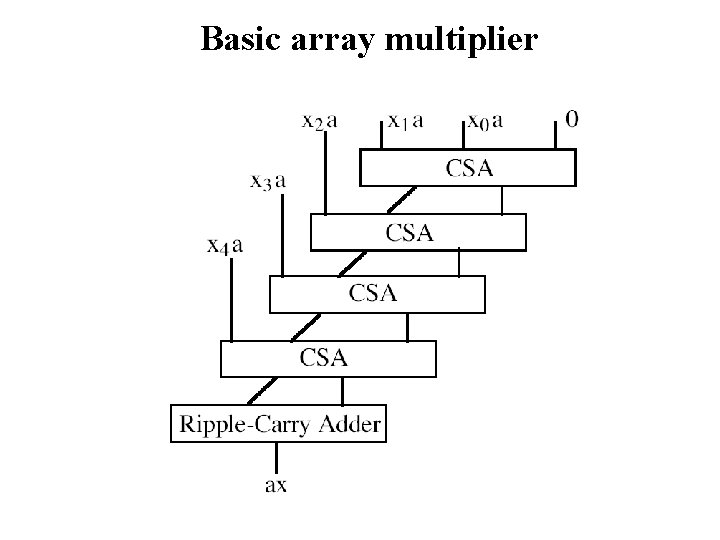
Basic array multiplier

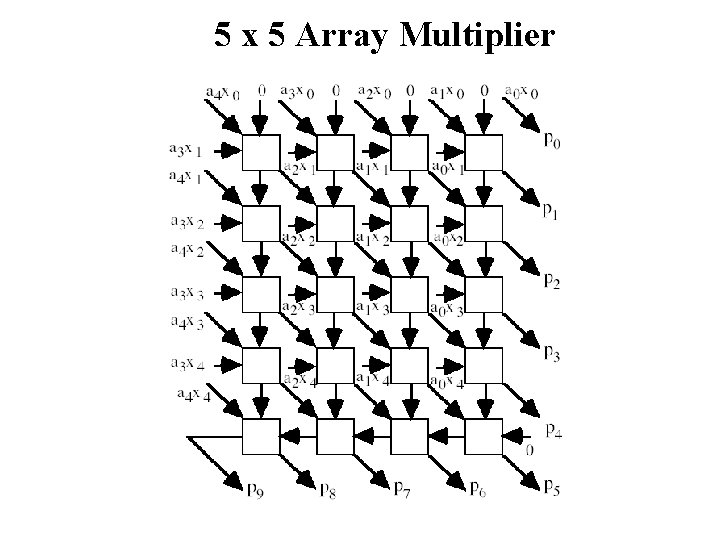
5 x 5 Array Multiplier

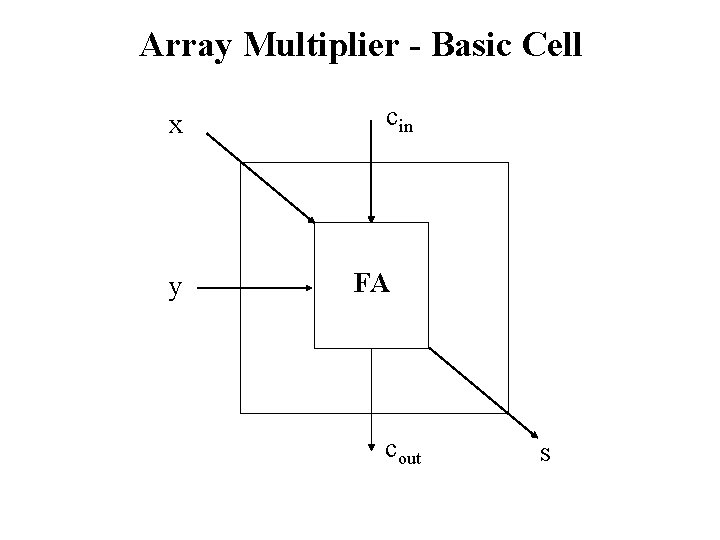
Array Multiplier - Basic Cell x y cin FA cout s

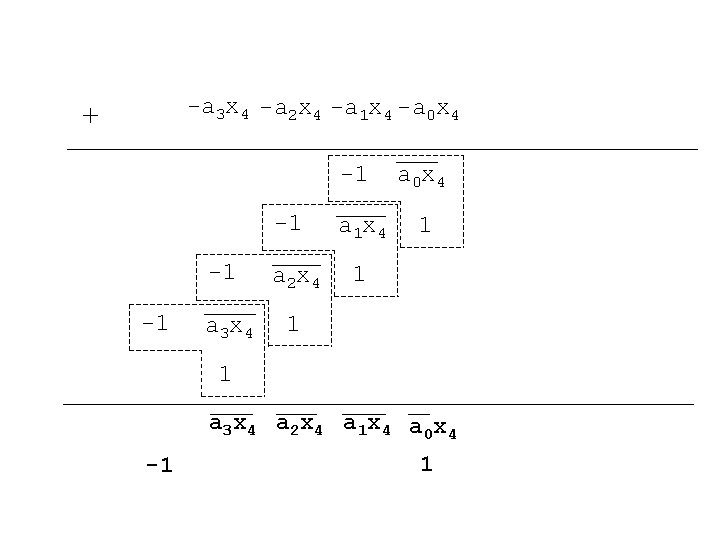
Baugh-Wooley 2’s Complement Multiplier x -a 4 a 3 a 2 a 1 a 0 -x 4 x 3 x 2 x 1 x 0 a 4 x 0 a 3 x 0 a 2 x 0 a 1 x 0 a 0 x 0 a 4 x 1 a 3 x 1 a 2 x 1 a 1 x 1 a 0 x 1 + a 4 x 2 a 3 x 2 a 2 x 2 a 1 x 2 a 0 x 2 a 4 x 3 a 4 x 4 a 3 x 4 a 4 x 4 1 p 9 p 8 p 7 -29 28 27 a 3 x 3 a 2 x 3 a 1 x 3 a 0 x 3 a 2 x 4 a 1 x 4 a 0 x 4 a 4 x 4 p 6 p 5 p 4 p 3 p 2 p 1 p 0 26 25 24 23 22 21 20

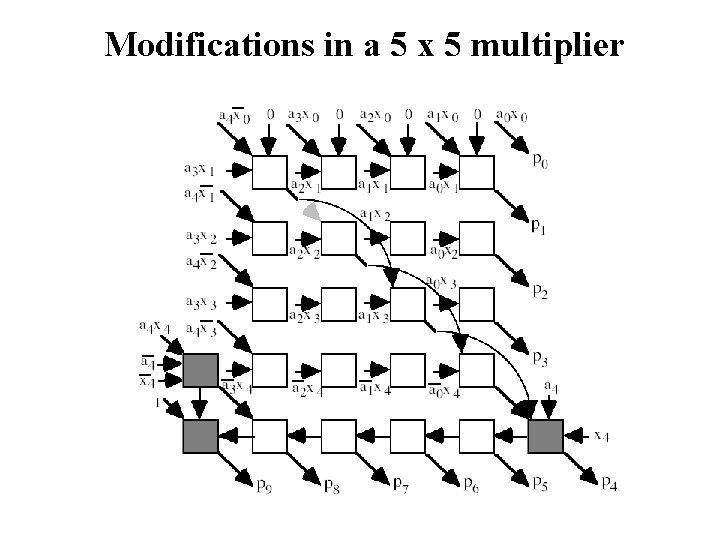
Modifications in a 5 x 5 multiplier

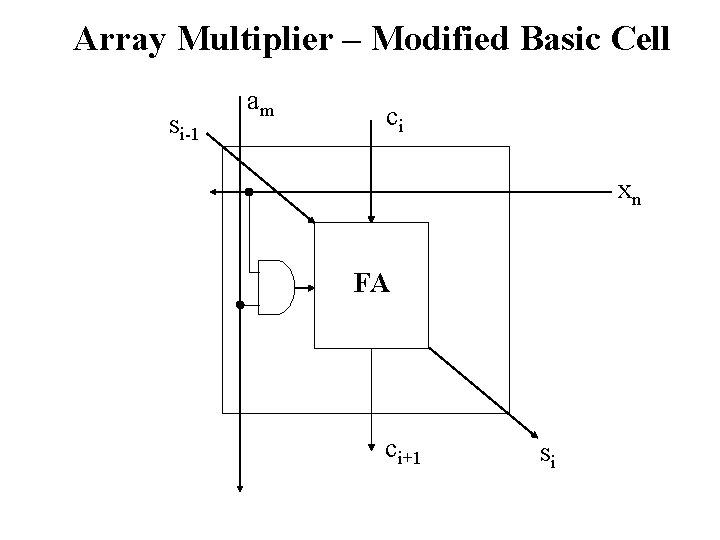
Array Multiplier – Modified Basic Cell si-1 am ci xn FA ci+1 si

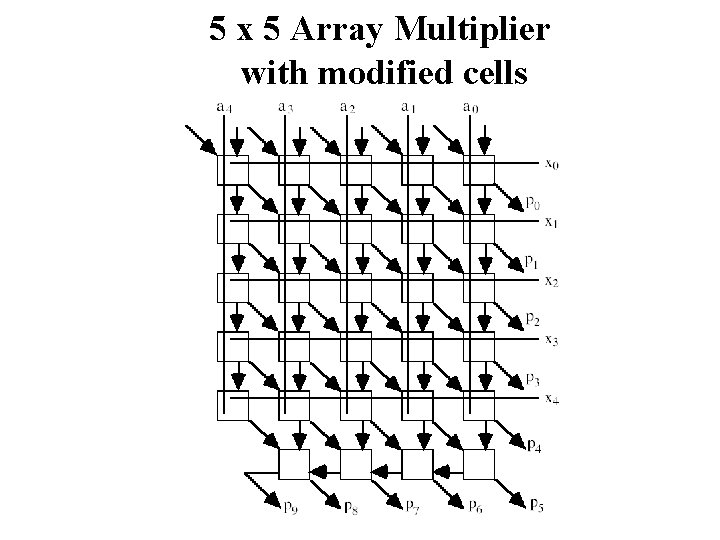
5 x 5 Array Multiplier with modified cells

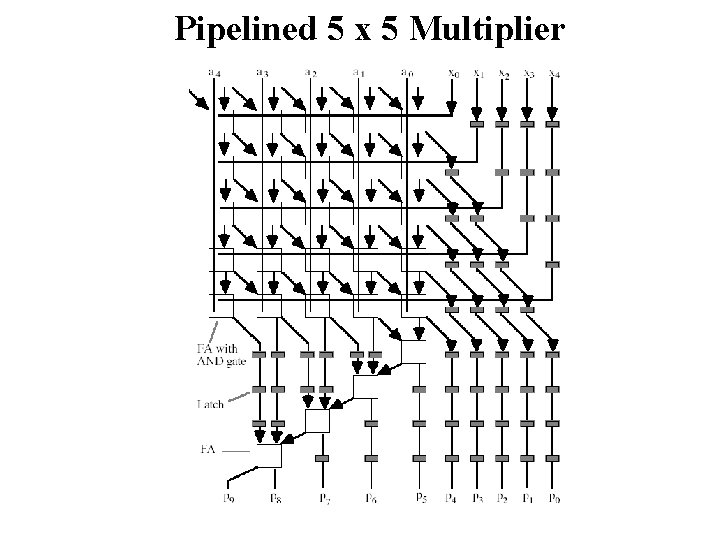
Pipelined 5 x 5 Multiplier

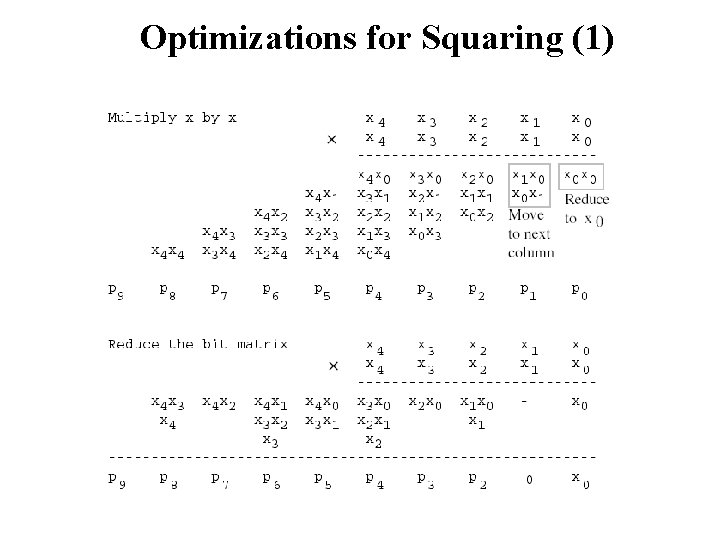
Optimizations for Squaring (1)

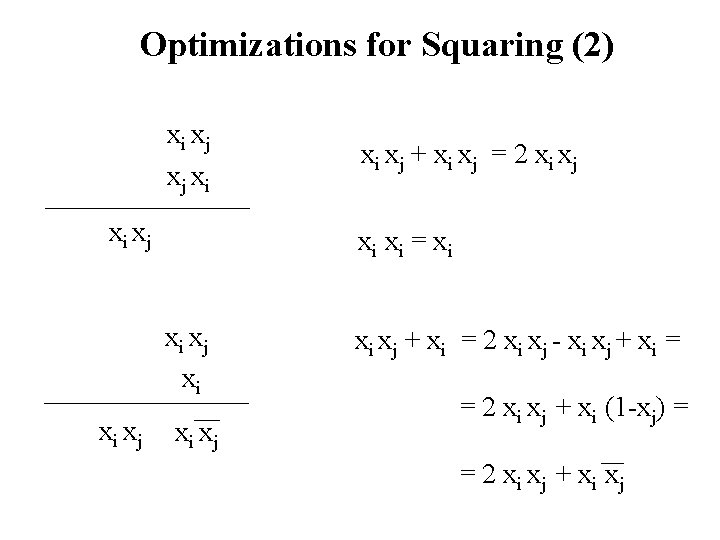
Optimizations for Squaring (2) xi xj xj xi xi = xi xi xj + xi xj = 2 xi xj + xi = 2 xi xj - xi xj + xi = = 2 xi xj + xi (1 -xj) = = 2 xi xj + xi xj

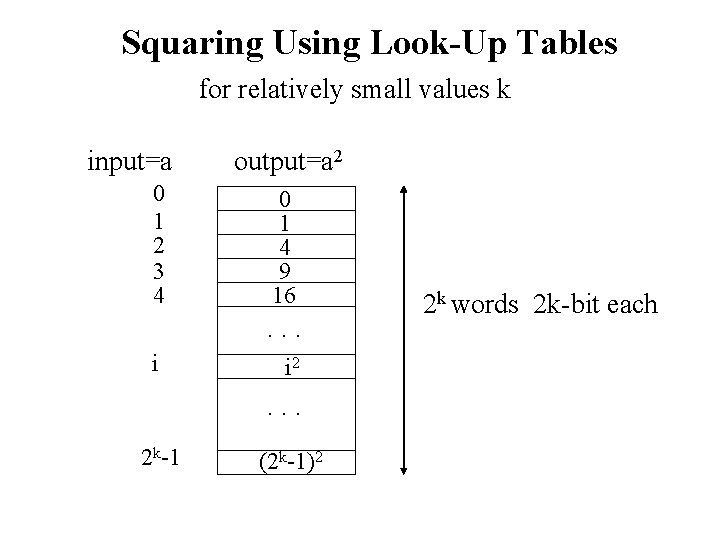
Squaring Using Look-Up Tables for relatively small values k input=a 0 1 2 3 4 output=a 2 0 1 4 9 16 . . . i i 2 . . . 2 k-1 (2 k-1)2 2 k words 2 k-bit each

Multiplication Using Squaring (a+x)2 - (a-x)2 a x= 4