LECTURE 7 TIME SERIES ANALYSIS Time Domain Models

LECTURE 7 TIME SERIES ANALYSIS Time Domain Models: Red Noise; AR and ARMA models Supplementary Readings: Wilks, chapters 8

Recall: Statistical Model [Observed Data] = [Signal] + [Noise] “noise” has to satisfy certain properties! If not, we must iterate on this process. . . We will seek a general method of specifying just such a model…

We conventionally assume Stationarity Statistics of the time series don’t change with time • Weak Stationarity (Covariance Stationarity) statistics are a function of lag k but not absolute time t • Cyclostationarity statistics are a periodic function of lag k • Strict Stationarity

Time Series Modeling All linear time series models can be written in the form: Autoregressive Moving-Average Model(“ARMA”) ARMA(K, M) MODEL Box and Jenkins (1976) We assume that e are Gaussian distributed.

Time Series Modeling All linear time series models can be written in the form: Consider Special case of simple Autoregressive AR(k) model (qm=0) Suppose k=1, and define f 1 r Special case of a Markov Process (a process for which the state of system depends on previous states) This should look familiar!

Time Series Modeling All linear time series models can be written in the form: Consider Special case of simple Autoregressive AR(k) model (qm=0) Suppose k=1, and define f 1 r Assume process is zero mean, then Lag-one correlated process or “AR(1)” process…

AR(1) Process For simplicity, we assume zero mean

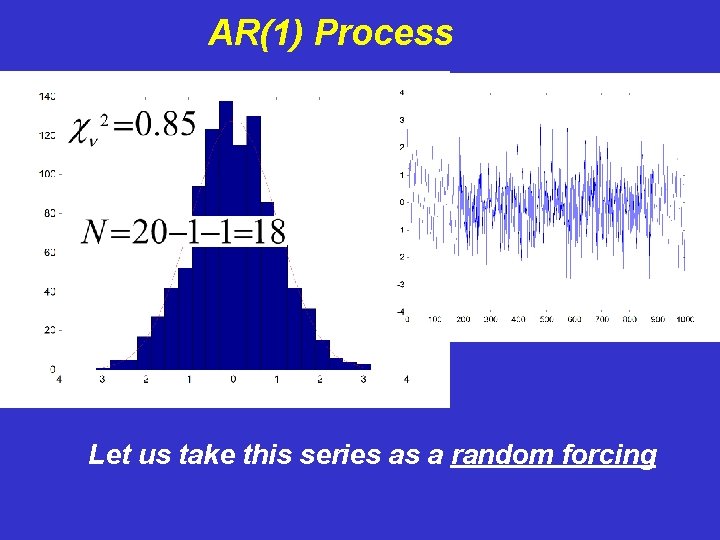
AR(1) Process Let us take this series as a random forcing

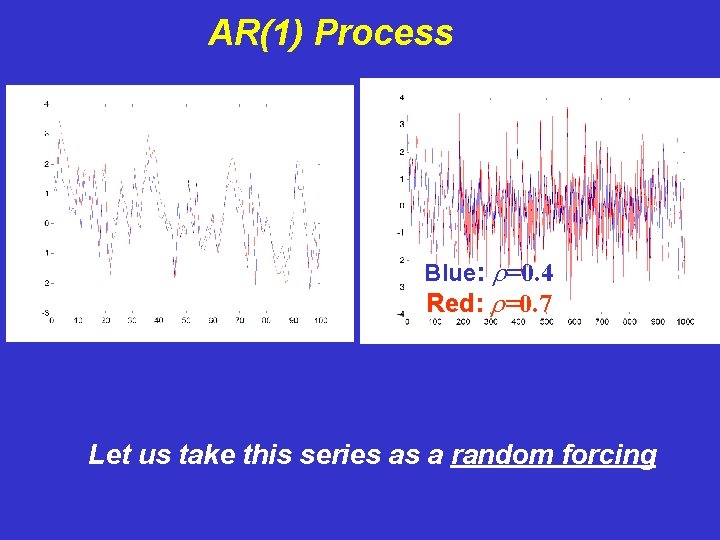
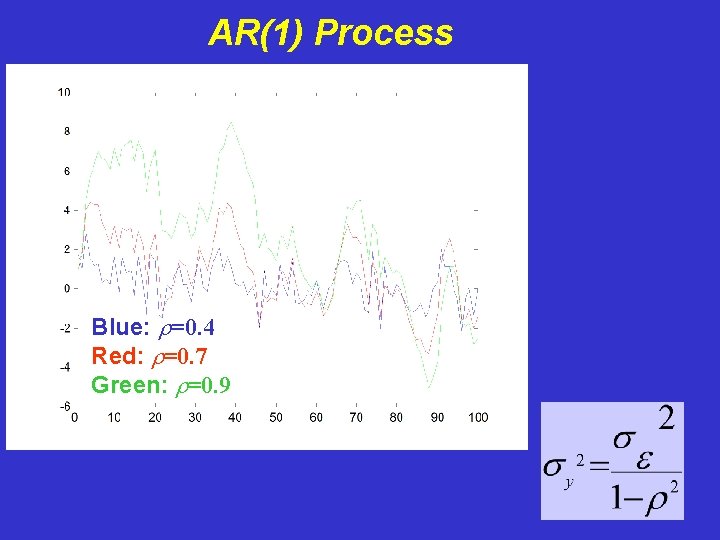
AR(1) Process Blue: r=0. 4 Red: r=0. 7 Let us take this series as a random forcing

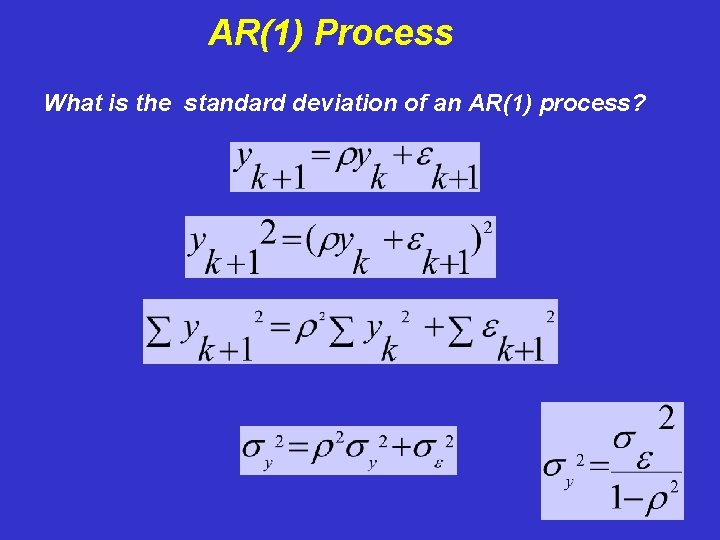
AR(1) Process What is the standard deviation of an AR(1) process?

AR(1) Process Blue: r=0. 4 Red: r=0. 7 Green: r=0. 9

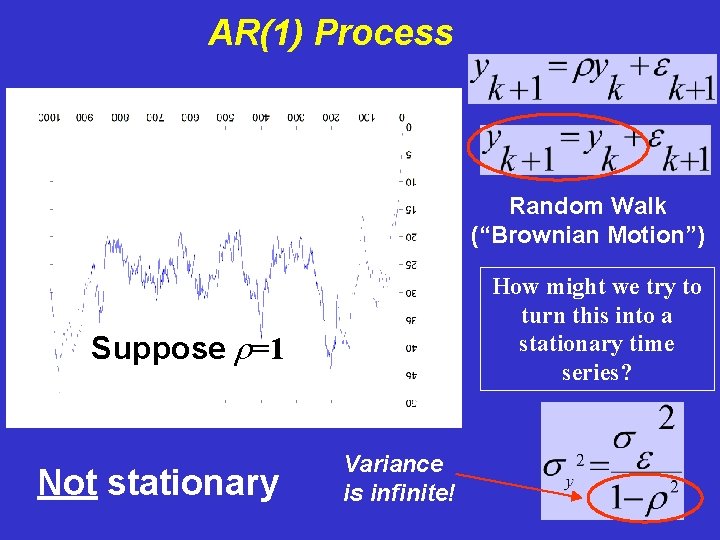
AR(1) Process Random Walk (“Brownian Motion”) How might we try to turn this into a stationary time series? Suppose r=1 Not stationary Variance is infinite!

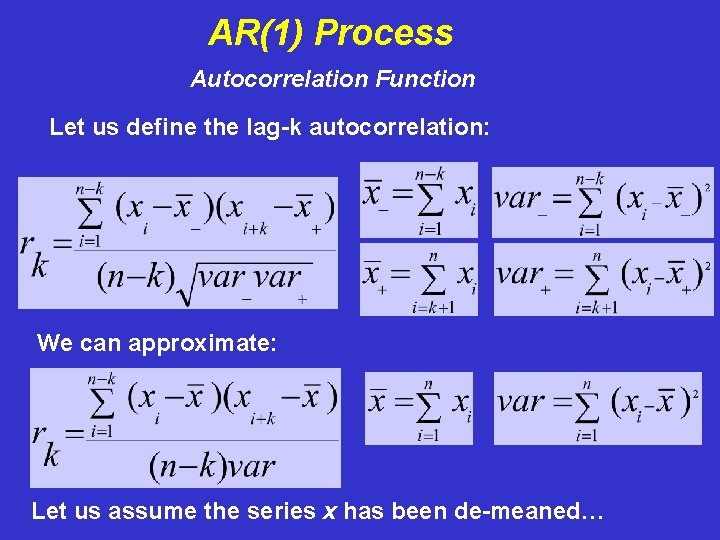
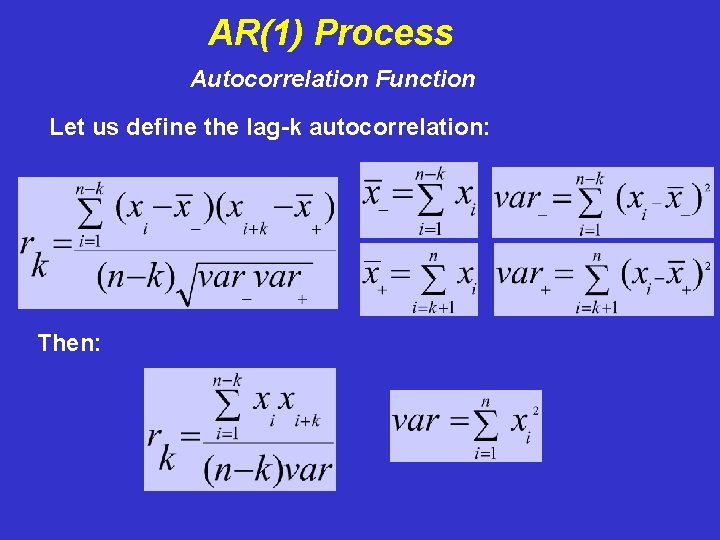
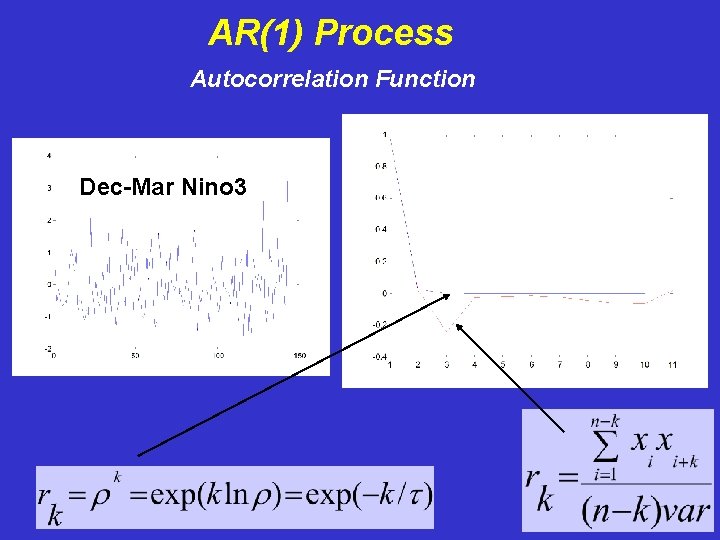
AR(1) Process Autocorrelation Function Let us define the lag-k autocorrelation: We can approximate: Let us assume the series x has been de-meaned…

AR(1) Process Autocorrelation Function Let us define the lag-k autocorrelation: Then:

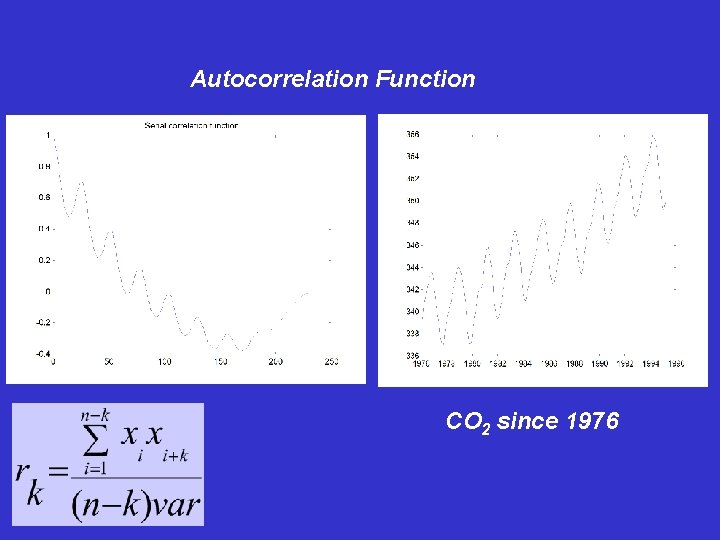
Autocorrelation Function CO 2 since 1976

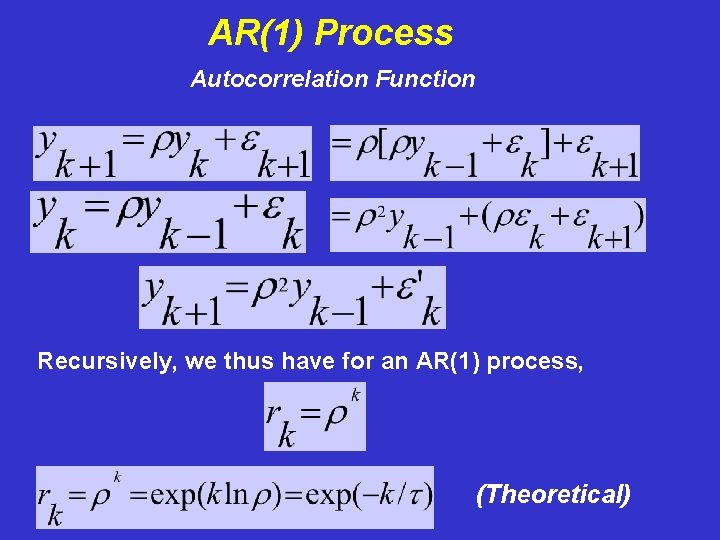
AR(1) Process Autocorrelation Function Recursively, we thus have for an AR(1) process, (Theoretical)

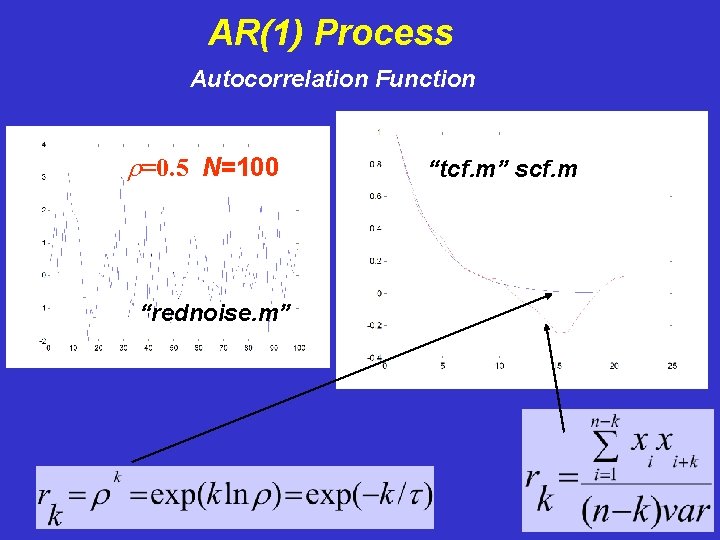
AR(1) Process Autocorrelation Function r=0. 5 N=100 “rednoise. m” “tcf. m” scf. m

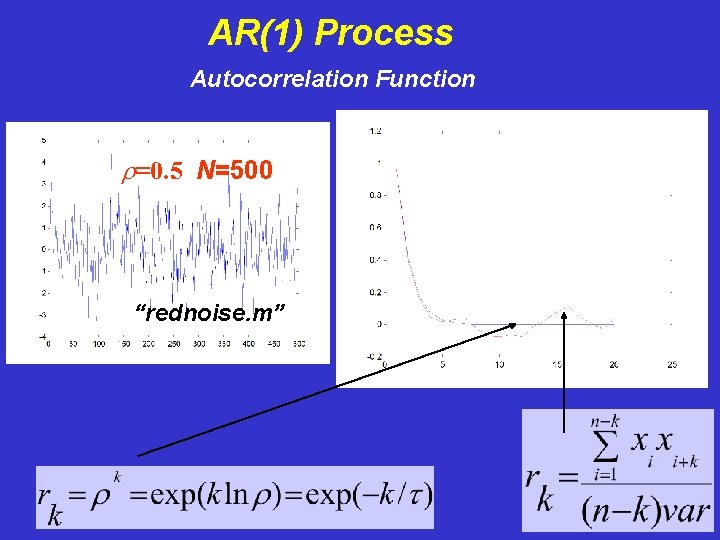
AR(1) Process Autocorrelation Function r=0. 5 N=100 N=500 “rednoise. m”

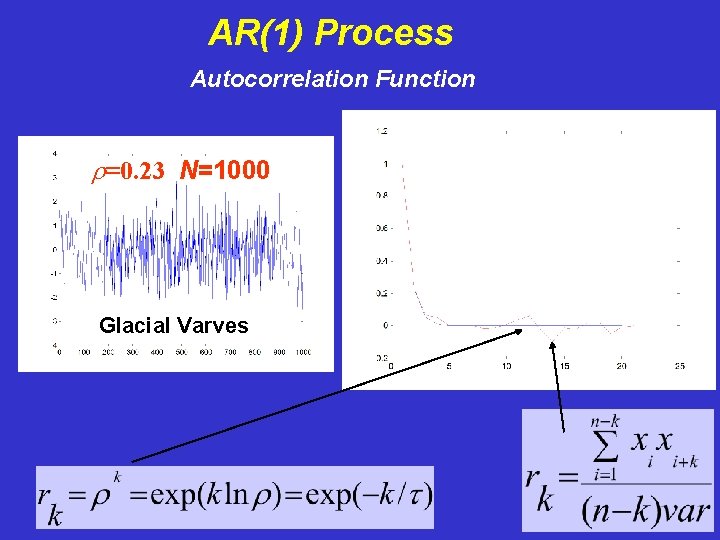
AR(1) Process Autocorrelation Function r=0. 23 N=1000 Glacial Varves

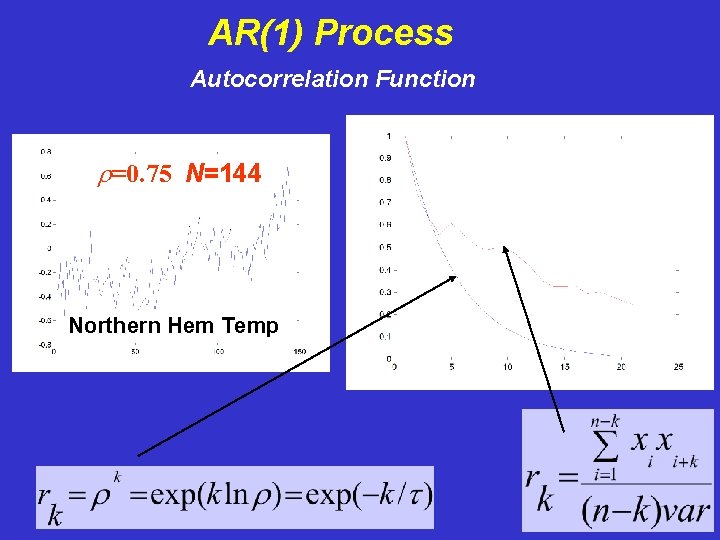
AR(1) Process Autocorrelation Function r=0. 75 N=144 Northern Hem Temp

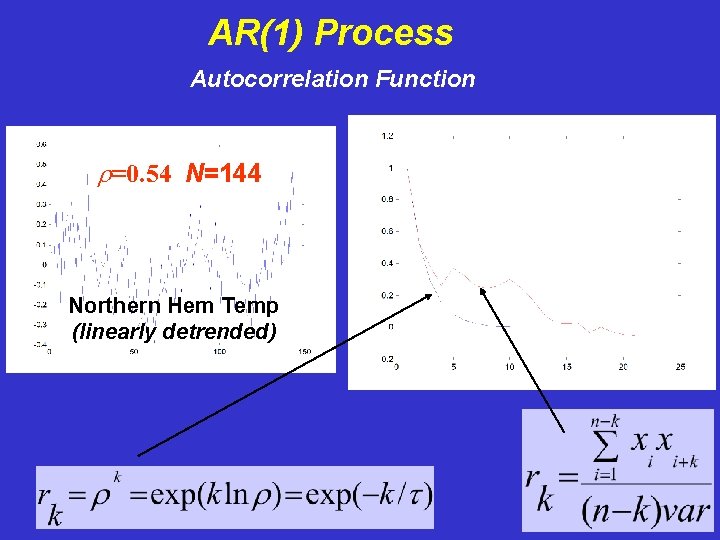
AR(1) Process Autocorrelation Function r=0. 54 N=144 Northern Hem Temp (linearly detrended)

AR(1) Process Autocorrelation Function Dec-Mar Nino 3

AR(1) Process The sampling distribution for r is given by the sampling distribution for the slope parameter in linear regression!

AR(1) Process The sampling distribution for r is given by the sampling distribution for the slope parameter in linear regression! How do we determine if r is significantly non-zero? This is just the t test!

AR(1) Process When Serial Correlation is Present, the variance of the mean must be adjusted, Variance inflation factor Recall for AR(1) series, This effects the significance of regression/correlation as we saw previously…

AR(1) Process Suppose r 1 This effects the significance of regression/correlation as we saw previously…

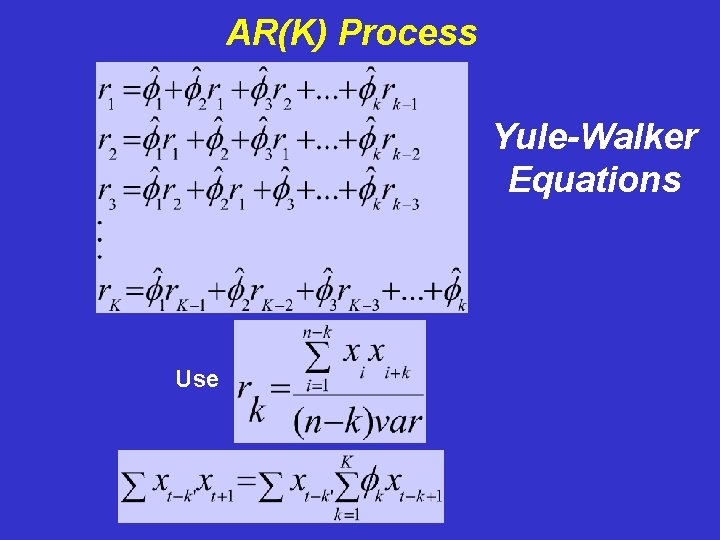
Now consider an AR(K) Process For simplicity, we assume zero mean Multiply this equation by xt-k’ and sum,

AR(K) Process Yule-Walker Equations Use

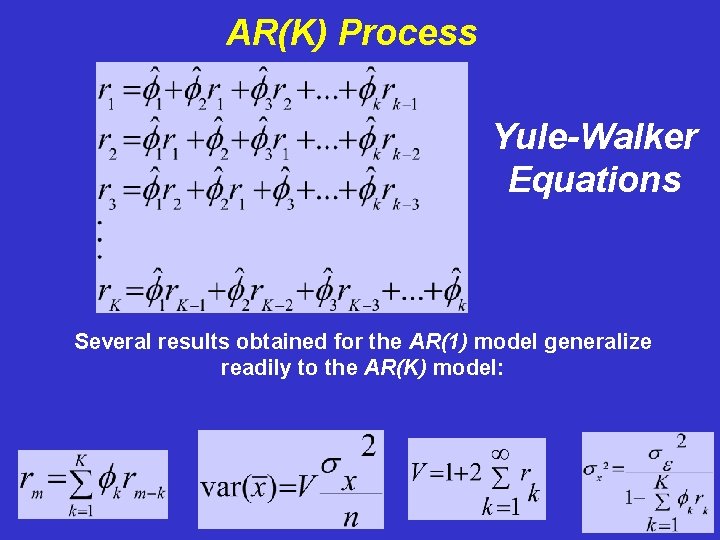
AR(K) Process Yule-Walker Equations Several results obtained for the AR(1) model generalize readily to the AR(K) model:

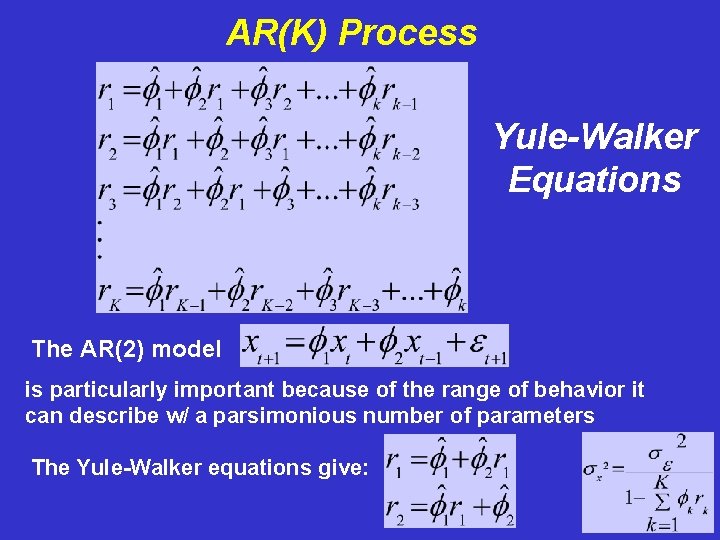
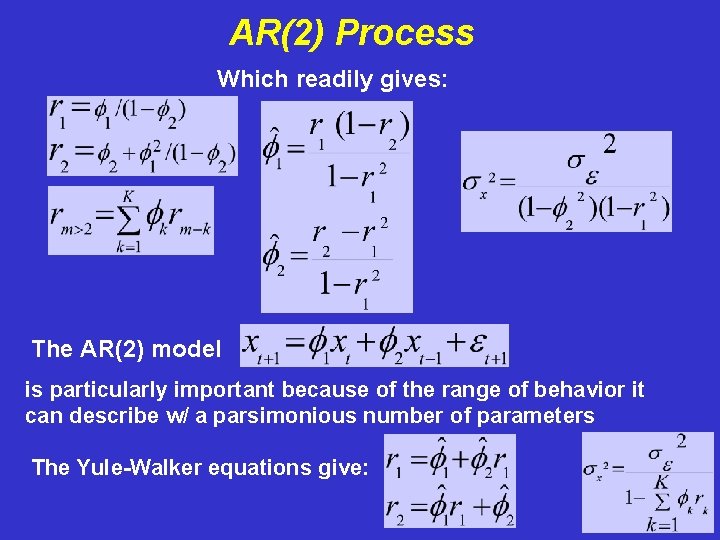
AR(K) Process Yule-Walker Equations The AR(2) model is particularly important because of the range of behavior it can describe w/ a parsimonious number of parameters The Yule-Walker equations give:

AR(2) Process Which readily gives: The AR(2) model is particularly important because of the range of behavior it can describe w/ a parsimonious number of parameters The Yule-Walker equations give:

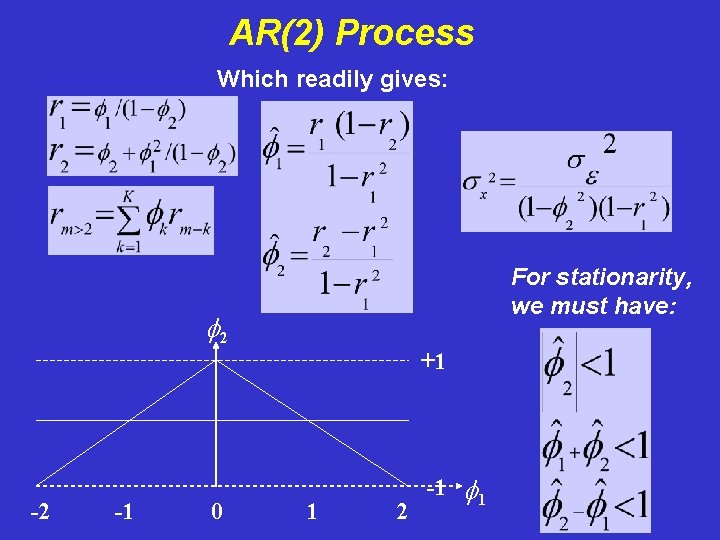
AR(2) Process Which readily gives: For stationarity, we must have: f 2 +1 -2 -1 0 1 2 -1 f 1

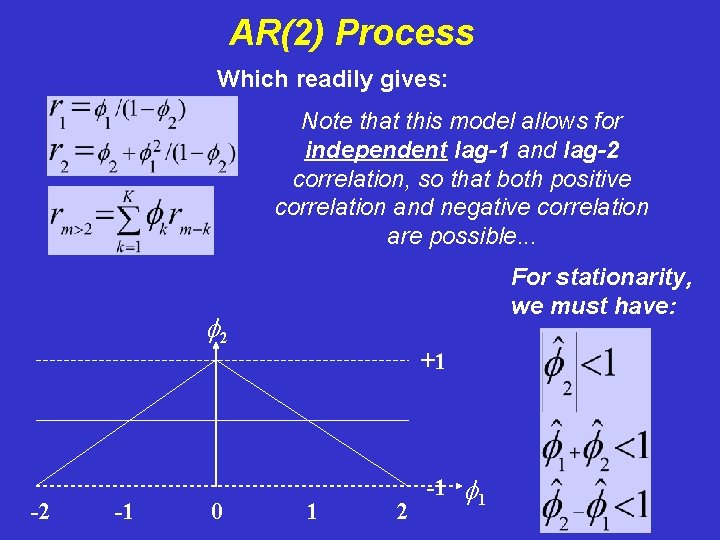
AR(2) Process Which readily gives: Note that this model allows for independent lag-1 and lag-2 correlation, so that both positive correlation and negative correlation are possible. . . For stationarity, we must have: f 2 +1 -2 -1 0 1 2 -1 f 1

AR(2) Process Which readily gives: Note that this model allows for independent lag-1 and lag-2 correlation, so that both positive correlation and negative correlation are possible. . . “artwo. m” For stationarity, we must have:

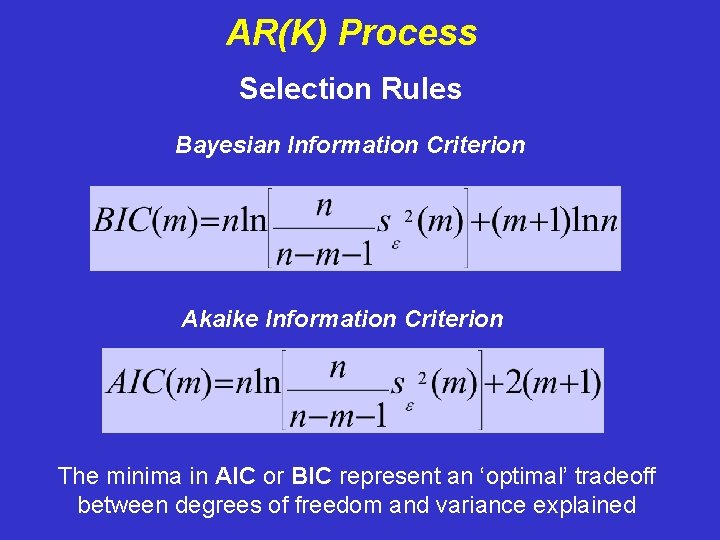
AR(K) Process Selection Rules Bayesian Information Criterion Akaike Information Criterion The minima in AIC or BIC represent an ‘optimal’ tradeoff between degrees of freedom and variance explained

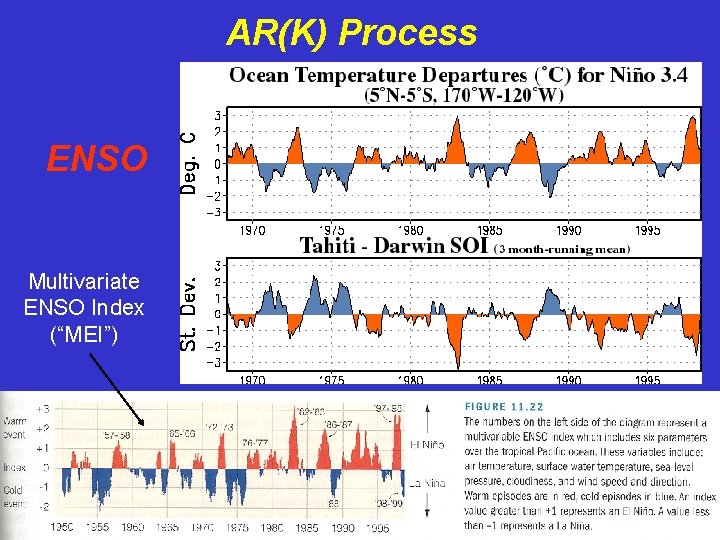
AR(K) Process ENSO Multivariate ENSO Index (“MEI”)

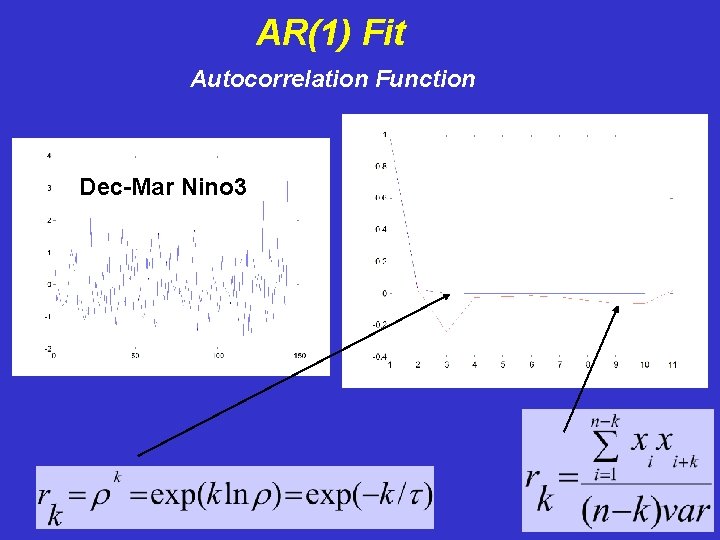
AR(1) Fit Autocorrelation Function Dec-Mar Nino 3

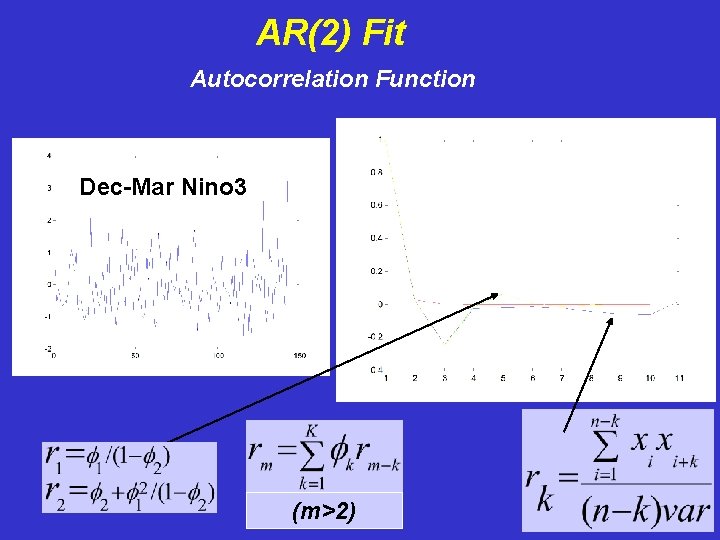
AR(2) Fit Autocorrelation Function Dec-Mar Nino 3 (m>2)

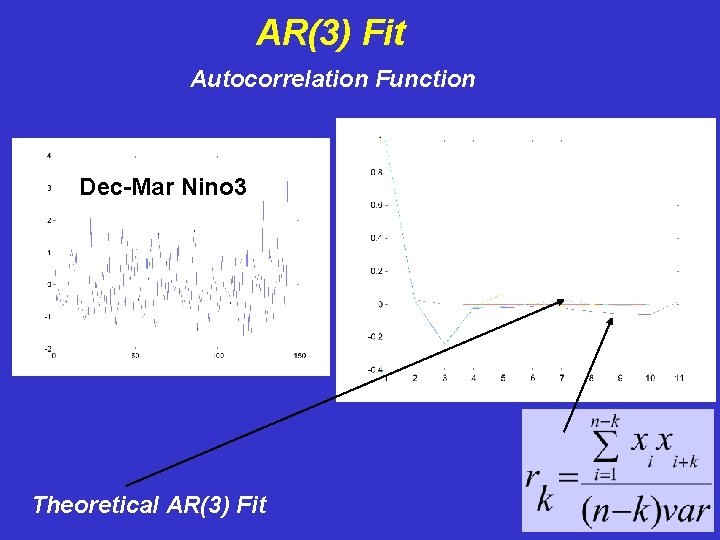
AR(3) Fit Autocorrelation Function Dec-Mar Nino 3 Theoretical AR(3) Fit

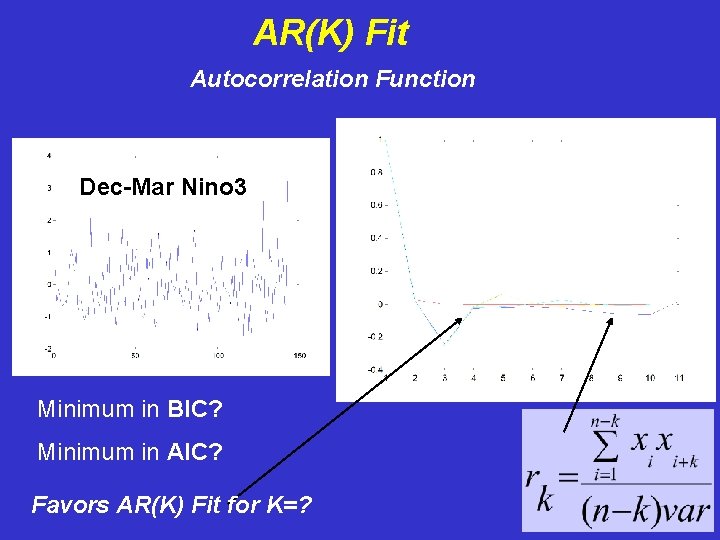
AR(K) Fit Autocorrelation Function Dec-Mar Nino 3 Minimum in BIC? Minimum in AIC? Favors AR(K) Fit for K=?

MA model Now, consider the case f k=0 Pure Moving Average (MA) model, represents a running mean of the past M values. Consider case where M=1…

MA(1) model Now, consider the case f k=0 Consider case where M=1…

ARMA(1, 1) model