Lecture 7 Intro to Machine Learning Rachel Greenstadt

Reminders • Machine Learning exercise out today • We’ll go over it • Due

Machine Learning • • Definition: the study of computer algorithms that improve automatically through

Where is ML useful? • Self-customizing software • spam filters, learning user preferences •

Learning element • Design of a learning element is affected by – Which components

Learning • Inductive Supervised • “Teacher” provides labeled examples • Opposite of unsupervised, e.

Machine Learning terms • Supervised examples • Training set : set of examples used

Inductive Learning • Construct/adjust h to agree with f on training set (the supervised

Induction Task Example • • • Given: 9714 patient records, each describing a pregnancy

Decision Trees • Representation: • Each internal node tests an attribute • Each branch

Expressiveness • Decision trees can express any function of the input attributes. • E.

Hypothesis spaces • How many distinct decision trees with n Boolean attributes? • =

Decision tree learning • Aim: find a small tree consistent with the training examples

Choosing an attribute • Idea: a good attribute splits the examples into subsets that

Learning decision trees • Problem: decide whether to wait for a table at a

Attribute-based representations • Examples described by attribute values (Boolean, discrete, continuous) • E. g.

Decision trees • One possible representation for hypotheses • E. g. , here is

Entropy • I(P(v 1), . . . , P(vn)) = Sumi=1. . n (-P(vi)log

Information gain • A chosen attribute A divides the training set E into subsets

Information gain • For the training set, p = n = 6, I(6/12, 6/12)

Example contd. • Decision tree learned from the 12 examples: • Substantially simpler than

Build a decision tree • Whether or not to move forward at an intersection,

Performance measurement • How do we know that h ≈ f ? 1. Use

Question • Suppose we generate a training set from a decision tree and then

Summary • Learning needed for unknown environments, lazy designers • Learning agent = performance

Bayesian Learning • Conditional probability • Bayesian classifiers • Assignment • Information Retrieval performance

Bayes’ Theorem • If P(h) > 0, then • P(h|d) = [P(d|h)P(h)]/P(d) • Can

Bayesian Exercises • Bayes: P(h|d) = [P(d|h)P(h)]/P(d) • Conditional: P(A|B) = P(A ^ B)/P(B)

Naive Bayesian • Why naive? Makes independence classifier assumptions which may not hold. .

Classifying reviews: Changeling • • Eastwood is a brilliant filmmaker who leaves nothing to

How to Classify? • Need to pick a set of features to use to

How to classify • Compute product of all conditional probabilities of each of the

$• Evaluating Your Classifier Precision - fraction of documents properly classified or positive$

Readings • Nilesh Dalvi, Pedro Domingos, Mausam Sumit, Sanghai Deepak Verma. Adversarial Classification. in

Slides: 45

Download presentation

Lecture 7 : Intro to Machine Learning Rachel Greenstadt & Mike Brennan November 10, 2008

Reminders • Machine Learning exercise out today • We’ll go over it • Due before class 11/24

Machine Learning • • Definition: the study of computer algorithms that improve automatically through experience Formally: • • Improve at task T with respect to performance measure P based on experience E Example: Learning to play Backgammon • • • T: play backgammon P: number of games won E: data about previously played games

Where is ML useful? • Self-customizing software • spam filters, learning user preferences • Data mining • medical records, credit fraud • Software that can’t be written by hand • speech recognition, autonomous driving • Other examples?

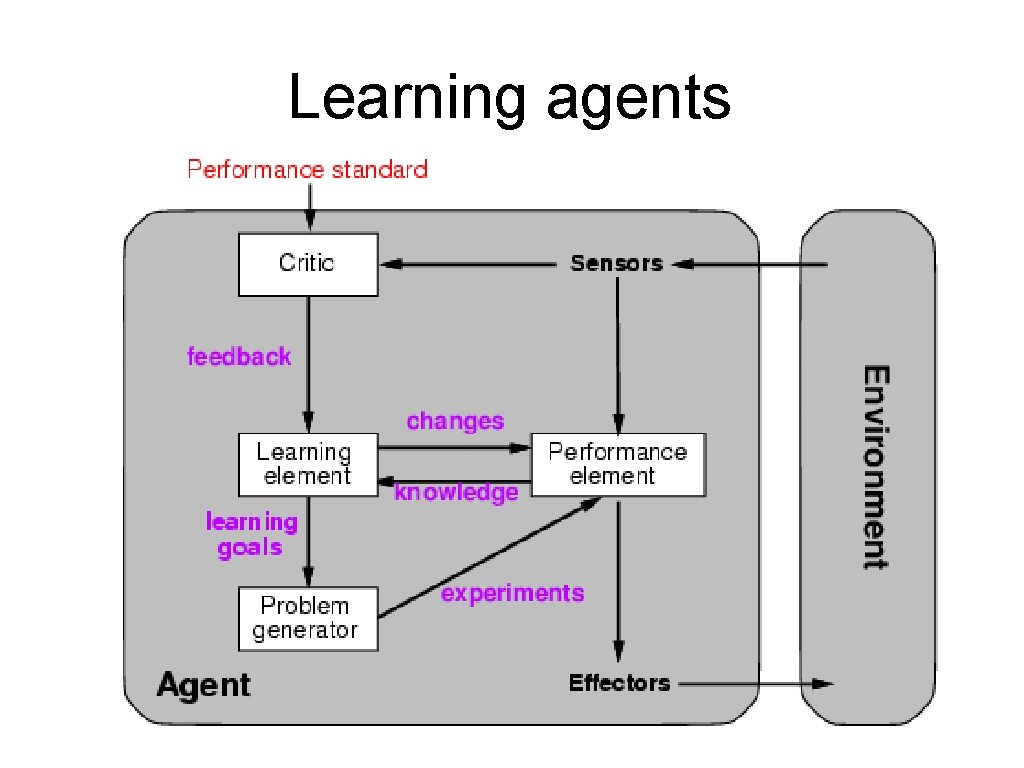
Learning agents

Learning element • Design of a learning element is affected by – Which components of the performance element are to be learned – What feedback is available to learn these components – What representation is used for the components • Type of feedback: – Supervised learning: correct answers for each example – Unsupervised learning: correct answers not given – Reinforcement learning: occasional rewards

Learning • Inductive Supervised • “Teacher” provides labeled examples • Opposite of unsupervised, e. g. clustering • Inductive Inference • Given: samples of an unknown function f • (x, f(x)) pairs • Goal: find a function h that approximates f

Machine Learning terms • Supervised examples • Training set : set of examples used to improve the algorithm • Test set : set of examples set aside to evaluate the algorithm based on performance measure

Inductive Learning • Construct/adjust h to agree with f on training set (the supervised examples) • (h is consistent if it agrees with f on all examples) • E. g. curve-fitting

Inductive Learning • Construct/adjust h to agree with f on training set (the supervised examples) • (h is consistent if it agrees with f on all examples) • E. g. curve-fitting Occam’s razor: prefer the simplest hypothesis consistent with the data

Induction Task Example • • • Given: 9714 patient records, each describing a pregnancy and a birth Each record contains 215 features Learn to predict which future patients are at high risk of C-section

Induction Task Example

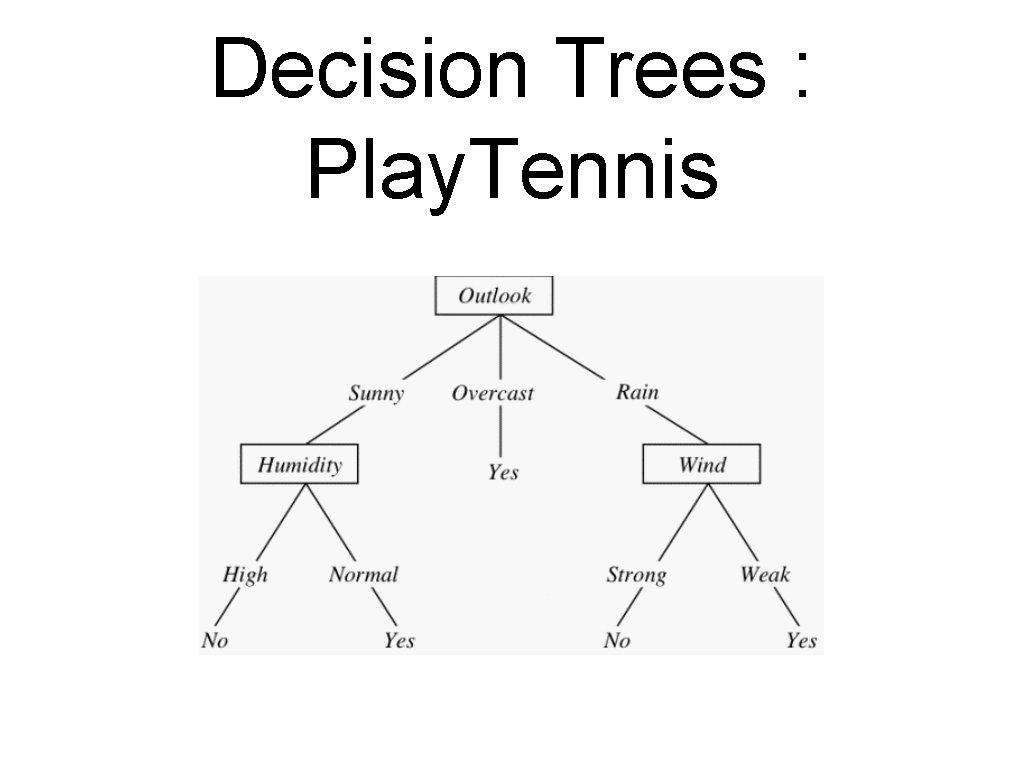
Decision Trees : Play. Tennis

Decision Trees • Representation: • Each internal node tests an attribute • Each branch is an attribute value • Each leaf assigns a classification

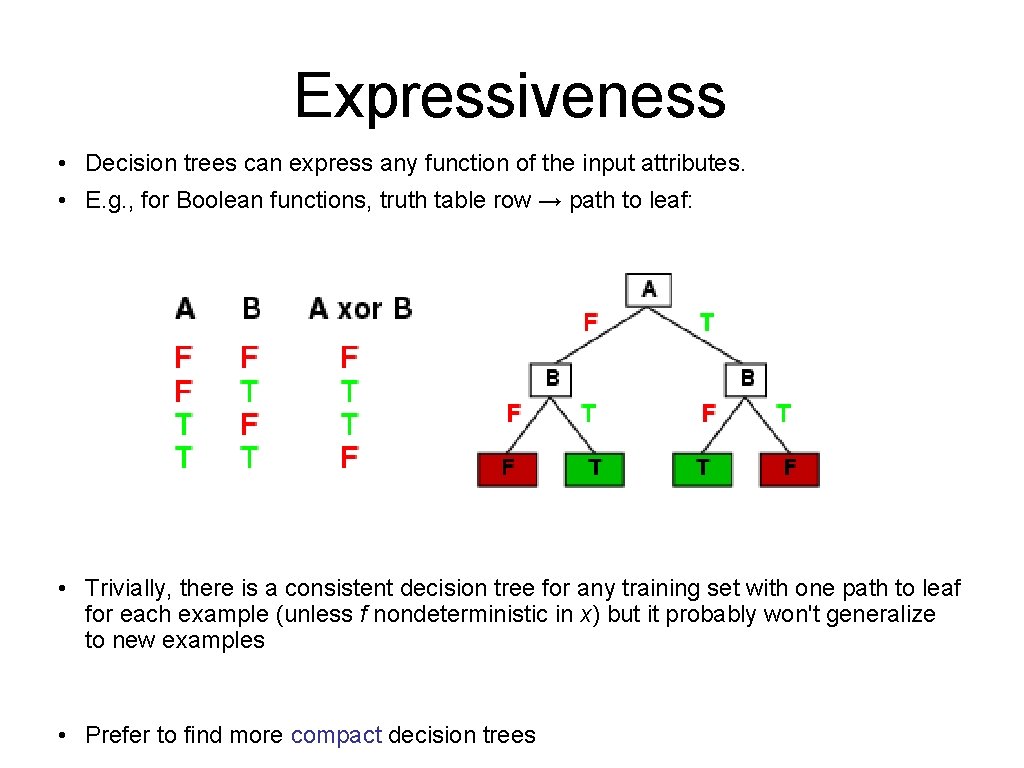
Expressiveness • Decision trees can express any function of the input attributes. • E. g. , for Boolean functions, truth table row → path to leaf: • Trivially, there is a consistent decision tree for any training set with one path to leaf for each example (unless f nondeterministic in x) but it probably won't generalize to new examples • Prefer to find more compact decision trees

Hypothesis spaces • How many distinct decision trees with n Boolean attributes? • = number of Boolean functions n n 2 • = number of distinct truth tables with 2 rows = 2 • E. g. , with 6 Boolean attributes, there are 18, 446, 744, 073, 709, 551, 616 trees • How many purely conjunctive hypotheses (e. g. , Hungry ∧¬Rain)? • Each attribute can be in (positive), in (negative), or out – ⇒ 3 n distinct conjunctive hypotheses • More expressive hypothesis space – increases chance that target function can be expressed – increases number of hypotheses consistent with training set – ⇒may get worse predictions

Decision tree learning • Aim: find a small tree consistent with the training examples • Idea: (recursively) choose "most significant" attribute as root of (sub)tree

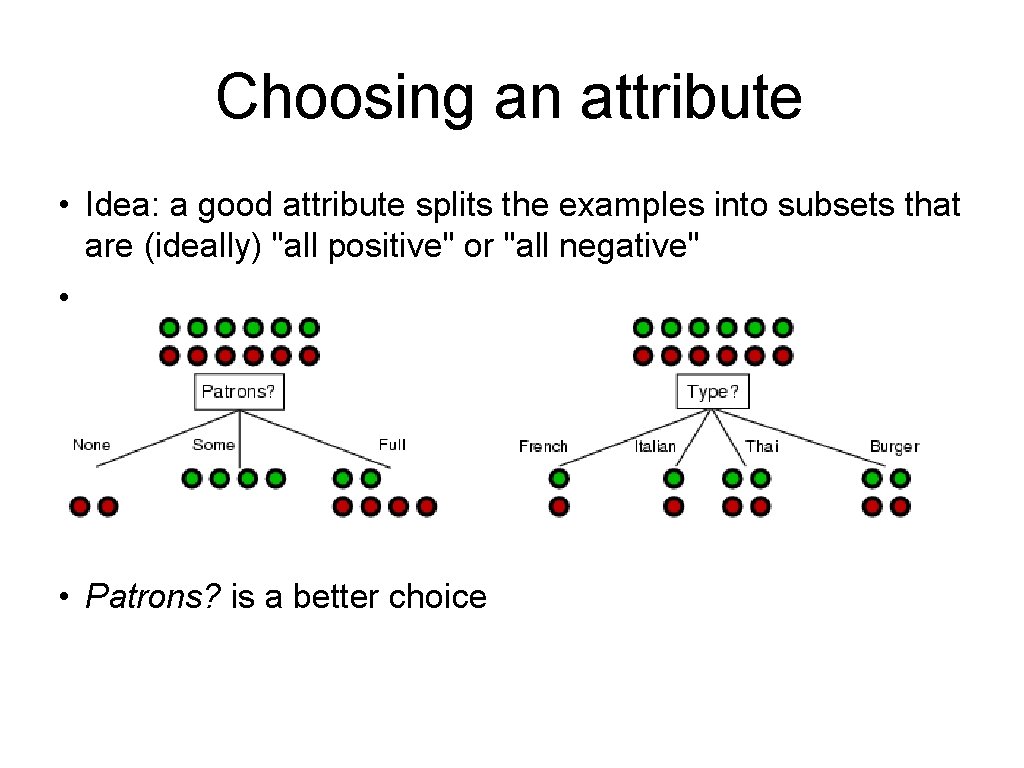
Choosing an attribute • Idea: a good attribute splits the examples into subsets that are (ideally) "all positive" or "all negative" • • Patrons? is a better choice

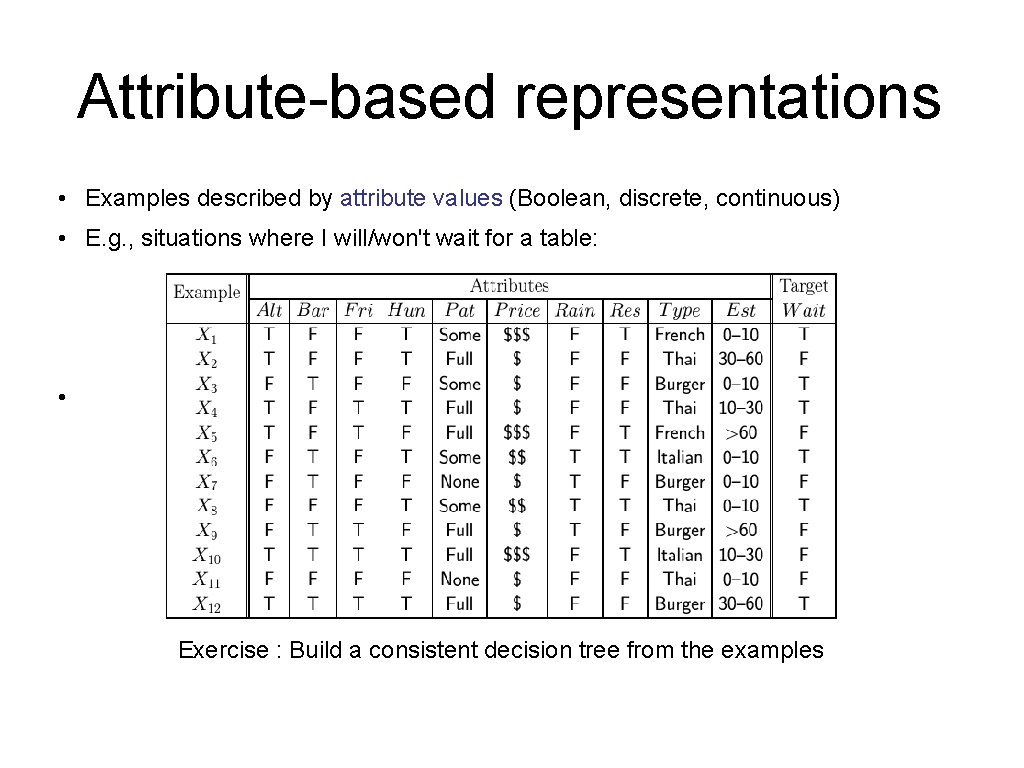
Learning decision trees • Problem: decide whether to wait for a table at a restaurant, based on the following attributes: 1. Alternate: is there an alternative restaurant nearby? 2. Bar: is there a comfortable bar area to wait in? 3. Fri/Sat: is today Friday or Saturday? 4. Hungry: are we hungry? 5. Patrons: number of people in the restaurant (None, Some, Full) 6. Price: price range ($, $$$) 7. Raining: is it raining outside? 8. Reservation: have we made a reservation? 9. Type: kind of restaurant (French, Italian, Thai, Burger) 10. Wait. Estimate: estimated waiting time (0 -10, 10 -30, 30 -60, >60)

Attribute-based representations • Examples described by attribute values (Boolean, discrete, continuous) • E. g. , situations where I will/won't wait for a table: • Exercise : Build a consistent decision tree from the examples

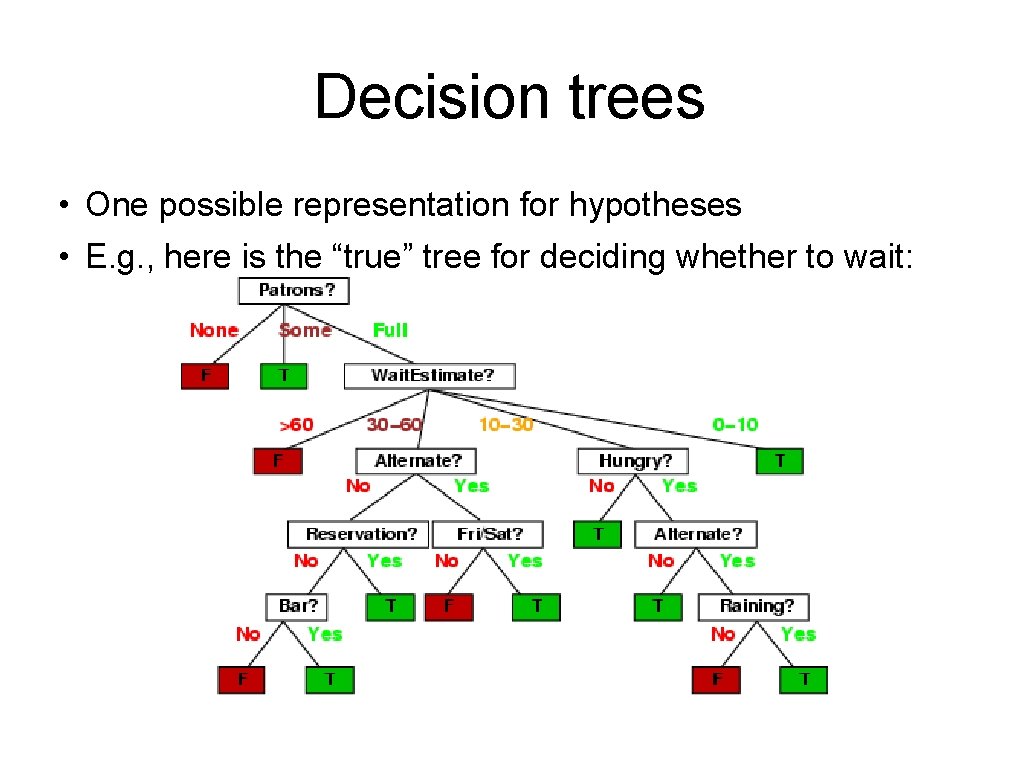
Decision trees • One possible representation for hypotheses • E. g. , here is the “true” tree for deciding whether to wait:

Entropy • I(P(v 1), . . . , P(vn)) = Sumi=1. . n (-P(vi)log 2 P(vi)) • Tossing a fair coin – I(1/2, 1/2) - 1/2 log 21/2 - 1/2 log 21/2 = 1 bit –If we weight the coin, information gain by tossing is reduced 25

Information gain • A chosen attribute A divides the training set E into subsets E 1, … , Ev according to their values for A, where A has v distinct values. • Information Gain (IG) or reduction in entropy from the attribute test: • remainder(A) is the remaining uncertainty after splitting on the attribute • Choose the attribute with the largest IG

Information gain • For the training set, p = n = 6, I(6/12, 6/12) = 1 bit • Consider the attributes Patrons and Type (and others too): • Patrons has the highest IG of all attributes and so is chosen by the DTL algorithm as the root

Example contd. • Decision tree learned from the 12 examples: • Substantially simpler than “true” tree---a more complex hypothesis isn’t justified by small amount of data

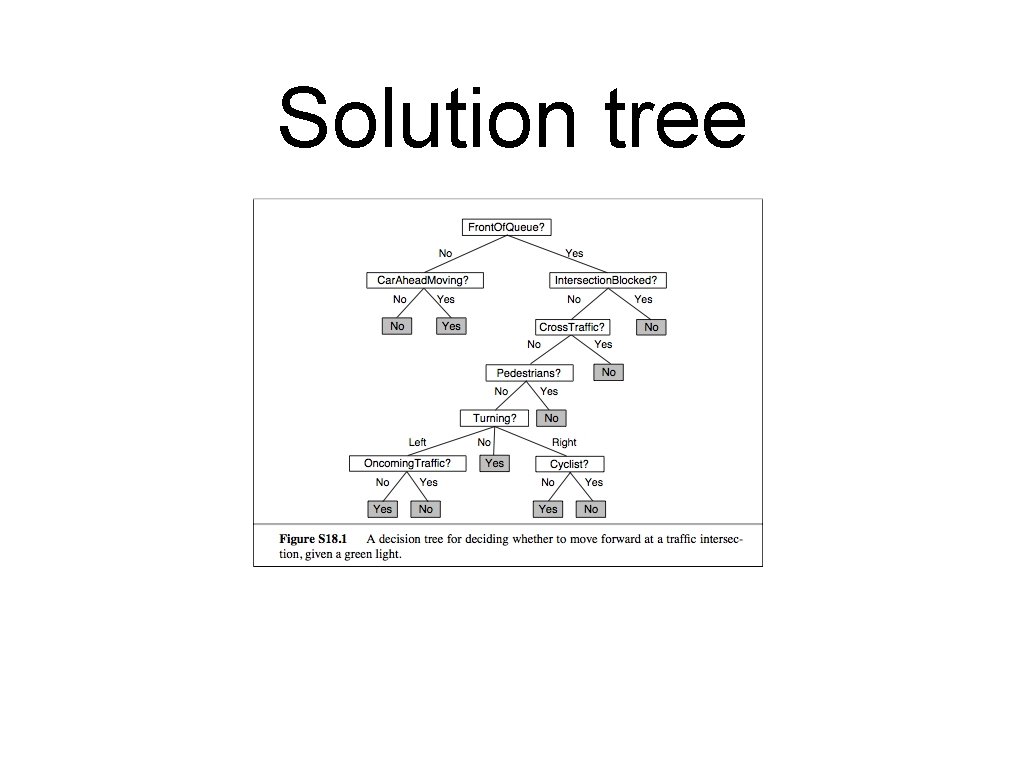
Build a decision tree • Whether or not to move forward at an intersection, given the light has just turned green. 29

Solution tree

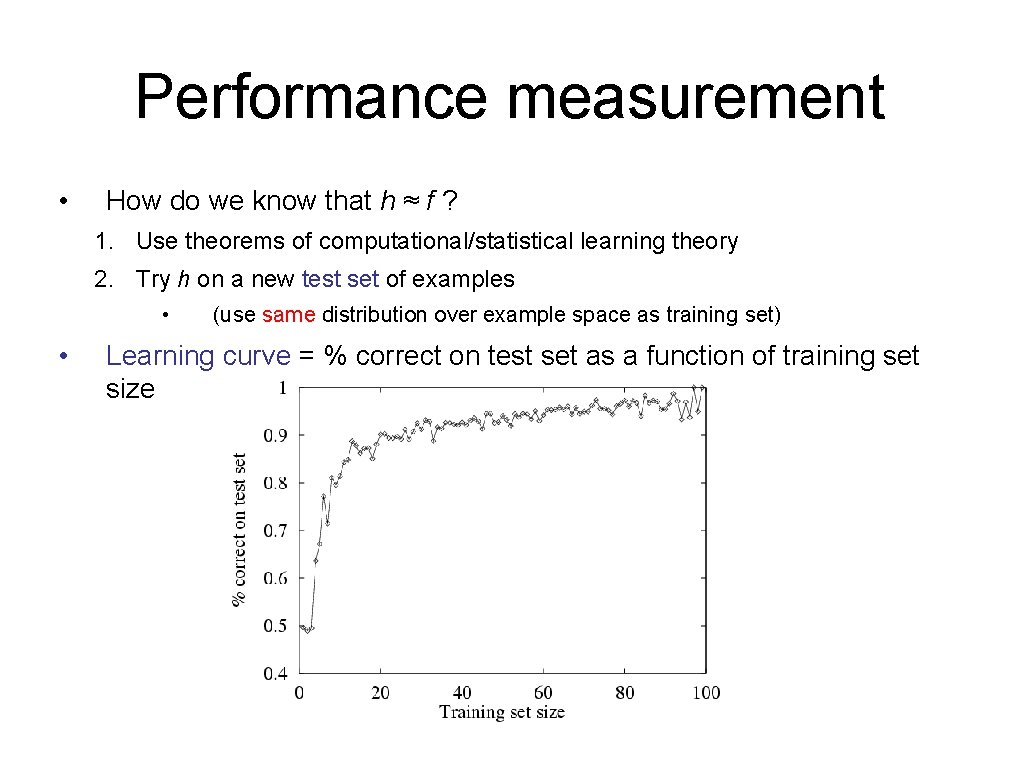
Performance measurement • How do we know that h ≈ f ? 1. Use theorems of computational/statistical learning theory 2. Try h on a new test set of examples • • (use same distribution over example space as training set) Learning curve = % correct on test set as a function of training set size

Question • Suppose we generate a training set from a decision tree and then apply decision tree learning to that training set. Is it the case that the learning algorithm will eventually return the correct tree as the training set goes to infinity? Why or why not? 32

Summary • Learning needed for unknown environments, lazy designers • Learning agent = performance element + learning element • For supervised learning, the aim is to find a simple hypothesis approximately consistent with training examples • Decision tree learning using information gain • Learning performance = prediction accuracy measured on test set

Bayesian Learning • Conditional probability • Bayesian classifiers • Assignment • Information Retrieval performance measures

Bayesian Exercises • Bayes: P(h|d) = [P(d|h)P(h)]/P(d) • Conditional: P(A|B) = P(A ^ B)/P(B) • • A patient takes a lab test and the result comes back positive. The test has a false negative rate of 2% and false positive rate of 2%. Furthermore, 0. 5% of the entire population have this cancer. What is the probability of cancer if we know the test result is positive? A math teacher gave her class two tests. 25% of the class passed both tests and 42% of the class passed the first test. What is the probability that a student who passed the first test also passed the second test?

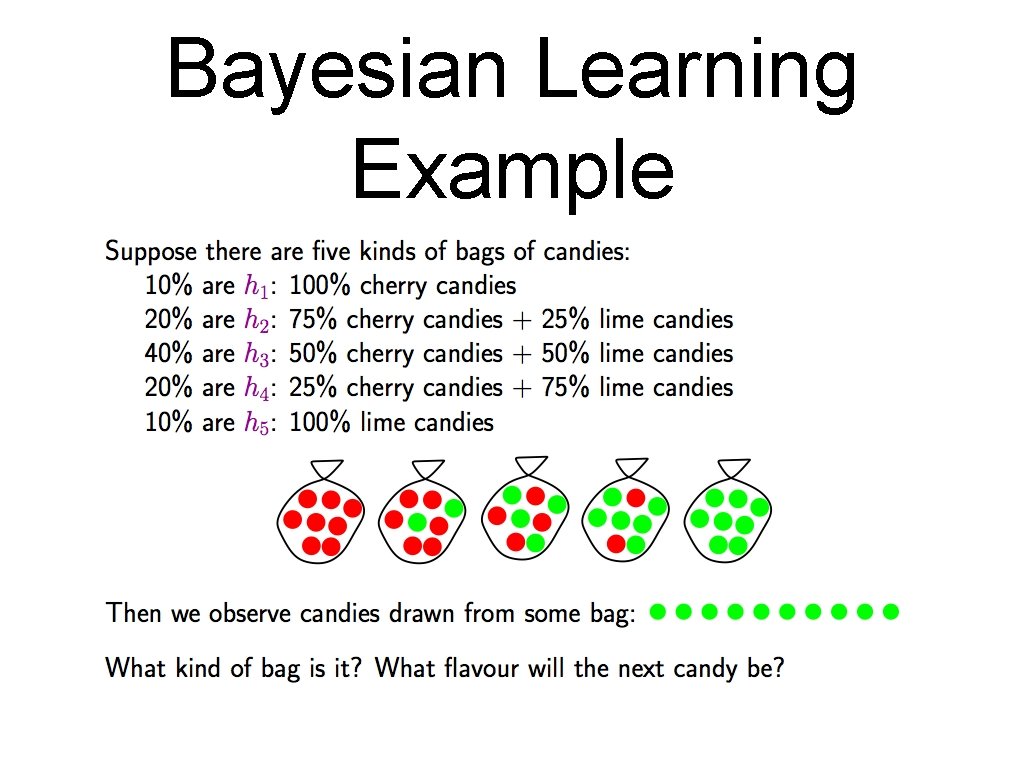
Bayesian Learning Example

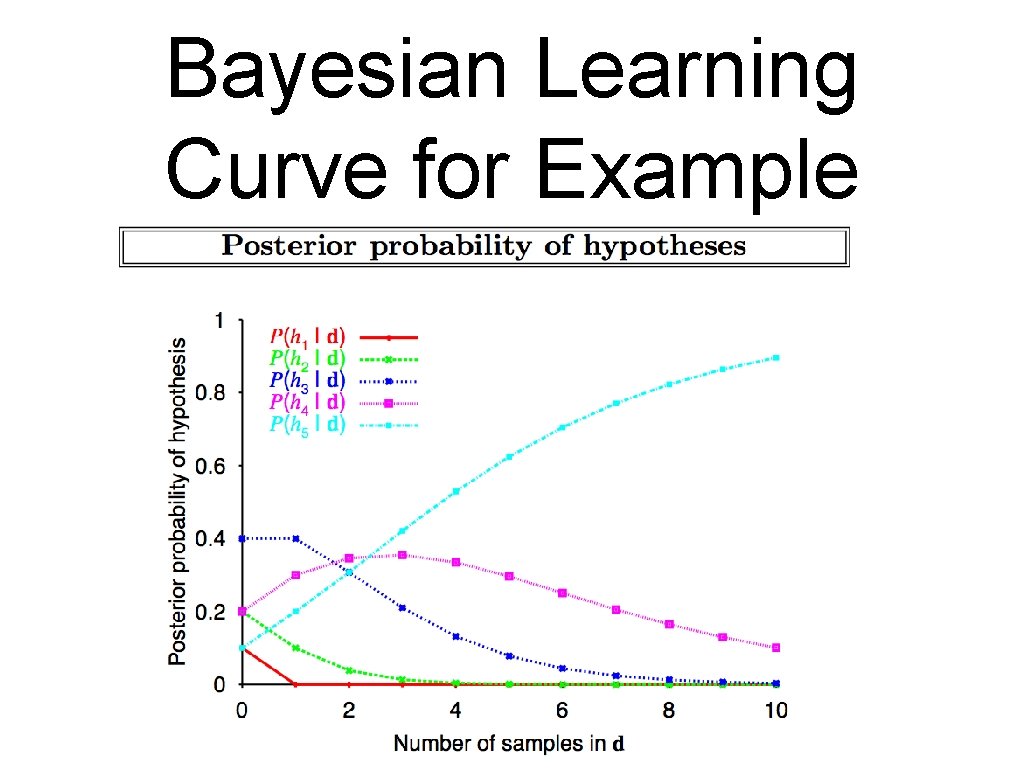
Bayesian Learning Curve for Example

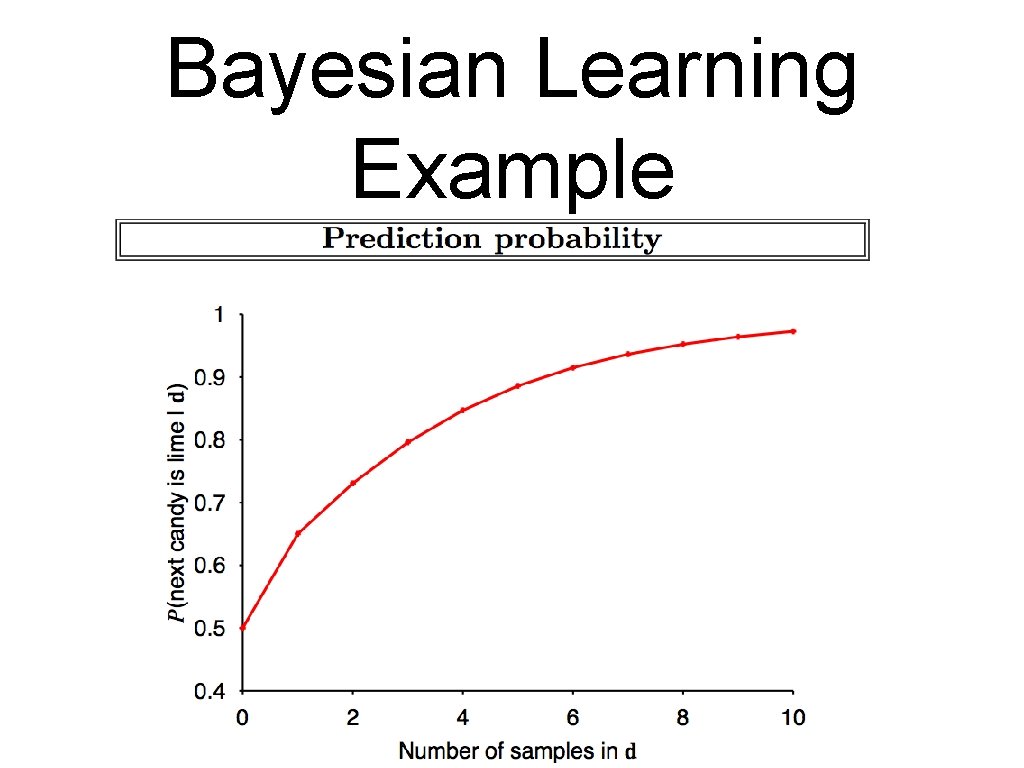
Bayesian Learning Example

Naive Bayesian • Why naive? Makes independence classifier assumptions which may not hold. . . • Goal : given a target, determine which class it belongs to, based on the prior probabilities of features in the target • In our case we’re looking to classify movie reviews as positive, negative, or neutral • Shouldn’t be too hard <200 lines of code

Classifying reviews: Changeling • • Eastwood is a brilliant filmmaker who leaves nothing to chance. The details of the era are sensational. Though gripping at times, the pace of the movie plods along with all deliberate speed that might prompt occasional glances at the wristwatch.

How to Classify? • Need to pick a set of features to use to distinguish positive and negative reviews • Starting feature : words, consider the frequency of words in positive and negative reviews • You will use this feature, and come up with one of your own

How to classify • Compute product of all conditional probabilities of each of the features of the document, multiplied by the prior probability of any document being a member of the class • Consider f a set of n features of document d

$• Evaluating Your Classifier Precision - fraction of documents properly classified or positive$

• Evaluating Your Classifier Precision - fraction of documents properly classified or positive predictive value • • Recall - the percentage of true positives (sensitivity) correctly identified • • True positives/(true positives + false positives) (True positives ^ Identified Positives) / True positives f-measure - the weighted harmonic mean of precision and recall • • F 1= (2 * precision * recall) / (precision + recall) More generally • • Fβ = [(1 + β 2) (precision * recall)]/(β 2 * precision + recall) Other things to think about: Proper sampling, cross validating.

Readings • Nilesh Dalvi, Pedro Domingos, Mausam Sumit, Sanghai Deepak Verma. Adversarial Classification. in Proceedings of the Tenth International Conference on Knowledge Discovery and Data Mining (KDD), 2004.