Lecture 7 Induction Sorting Today n Reading n

+ Lecture 7: Induction & Sorting

+ Today n Reading n JS Ch. 5. 2 – 5. 3 (Recursion, Design), Ch. 6 (Sorting) n Objectives n Induction n Correctness of Selection sort n Complexity of Selection sort

+ Announcements n Assignment 2 starter code posted n How to copy the starter code to my workspace? n Java. Doc – what’s expected? n Quiz on Friday n Big-O n Induction n Harvey Mudd Career Fair

+ Induction n Let n P(n) be some proposition To prove P(n) is true for all n ≥ 0 n (Step One) Base case: Prove P(0) n (Step Two) Assume P(k) is true for k ≥ 0 n (Step Three) Use this assumption to prove P(k+1).

+ Induction n Practice Examples n Prove 1+ 2 + … + n = [n(n+1)]/2 for all n ≥ 0 n Prove 20 + 21 + …+ 2 n = 2 n+1 – 1 for all n ≥ 0 n Prove 2 n < n! for all n ≥ 4 n Induction can be used to prove n Mathematical statements n Correctness of an algorithm n Complexity of an algorithm

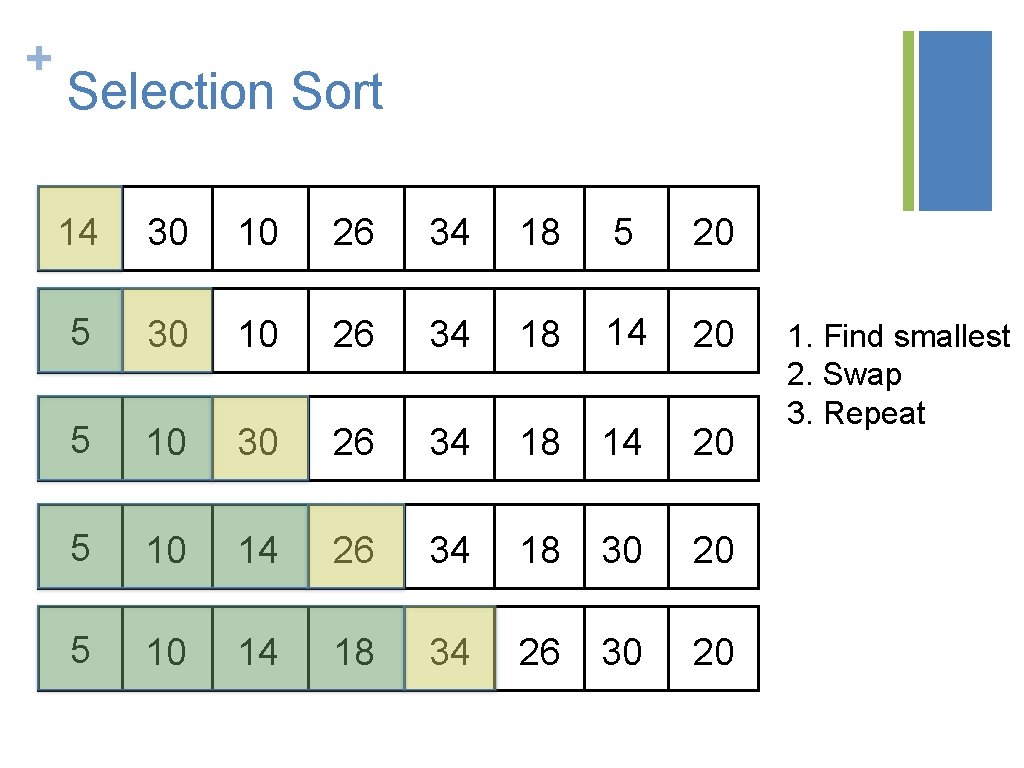
+ Selection Sort 14 30 10 26 34 18 5 20 5 30 10 26 34 18 14 20 5 10 30 26 34 18 14 20 5 10 14 26 34 18 30 20 5 10 14 18 34 26 30 20 1. Find smallest 2. Swap 3. Repeat

+ Selection Sort /** * Sorts an integer array using iterative selection sort * @param array of integers to be sorted */ private static void selection. Sort. Iterative(int[] array) { for(int i = 0; i < array. length; ++i) { int min = index. Of. Smallest(array, i); swap(array, i, min); } }

+ Selection Sort (helper) /** * @param array of integers * @param start. Index valid index into array * @return index of smallest value in array[start. Index. . . n] */ protected static int index. Of. Smallest(int[] array, int start. Index) { int smallest = start. Index; for(int i = start. Index+1; i < array. length; ++i) { if(array[i] < array[smallest]) { smallest = i; } } return smallest; }

+ Correctness of Selection Sort using Induction (on board) n Consider what must be true after every iteration of the for-loop in selection. Sort. Iterative

+ Complexity of Selection sort using Induction (on board) n Count the number of comparisons performed for each iteration of the for-loop in selection. Sort. Iterative

+ Strong Induction n Sometimes need to assume more than just the previous case, so instead n Prove P(0) n For n > 0, use P(k) for all k < n as assumption in order to prove P(n).

+ Proof Example n fast. Power(x, n) algorithm to calculate xn: n if n == 0 then return 1 n if n is even, return fast. Power(x*x, n/2) n if n is odd, return x*fast. Power(x, n-1) n Proof by induction on n (on board) n Base case: n ==0 n Induction case: Assume fast. Power(x, k) is xk for all k < n. Show fast. Power(x, n) is xn

+ Extra Slides

+ Insertion. Sort n Similar: To sort array of n elements: n Sort first n-1 elements n Insert last element in correct position n How long to insert new element into sorted list of n elements?

+ Complexity of Selection sort using Induction n Selection. Sort(array, n-1) nn n = array. length Takes time n(n-1)/2, n Results n Iterative in O(n 2) complexity version of selection sort is in text.

+ Complexity of Selection sort using Induction n Count number of comparisons of elts from array n n All comparisons are in index. Of. Largest(array, n) n At most n comparisons. Prove # of comparisons in selection. Sort(array, n) is 1 + 2 +. . . + n. n Base case: n = 0: No comparisons n Assume true for selection. Sort(array, k-1): 1 + 2 +. . . + (k-1) n Show for k elements: n index. Of. Largest(array, k) takes k comparisons, n swap takes none. n By induction selection. Sort(array, k-1) takes 1 + 2 +. . . +(k 1). n Therefore total: 1 + 2 +. . . + (k-1) + k

+ Complexity of Selection Sort n Count the number of comparisons of elements

+ Weekly Assignment 2 n Build Frequency Lists: Draw pictures. n Significantly harder than last lab. Use TA’s on Wednesday and Thursday nights. n Lab will be filled on Sunday night with CS 51 students! n Friday quiz

+ Correctness n For all n ≥ 0 where n < array. length, after running selection. Sort(array, n), array[0. . n] is sorted in non-descending order. n P(n): After running selection. Sort(array, n), array[0. . . n] is sorted in non-descending order. n Base case: prove P(0) n selection. Sort(array, 0) does nothing, but array[0. . 0] has only one element and hence is in order.

+ Induction Case n Suppose P(k) is true, i. e. after calling selection. Sort(array, k), the array[0. . k] is sorted in non-descending order n Prove P(k+1). n Call of selection. Sort(array, k+1) starts by finding index of largest element in array[0. . k+1] and swaps with element in array[k+1]. n By induction assumption, recursive call of selection. Sort(array, k) leaves array[0. . k] in order, and array[k+1] is larger, so array[0. . k+1] is in order. ✔