Lecture 7 Auctions serve the dual purpose of

Lecture 7 Auctions serve the dual purpose of eliciting preferences and allocating resources between competing uses. A less fundamental but more practical reason for studying auctions is that the value of goods exchanged each year by auction is huge. We describe the main kinds of auctions, define strategic and revenue equivalence, analyze optimal bidding behavior, and compare the outcomes from using different types. Read Chapters 19 and 20 of Strategic Play.

Auctions are widely used by companies, private individuals and government agencies to buy and sell commodities. They are also used in competitive contracting between an (auctioneer) firm and other (bidder) firms up or down the supply chain to reach trading agreements. Merger and acquisitions often have an auction flavor about them. To begin our discussion we compare two sealed bid auctions, where there are two bidders with known valuations of 2 and 4 respectively.

First price sealed bid auction In a first price sealed auction, players simultaneously submit their bids, the highest bidder wins the auction, and pays what she bid for the item. Highway contracts typically follow this form. For example, if the valuation 4 player bids 5 and the valuation 2 player bids 1, then the former wins the auction, pays 5 and makes a net loss of 1.

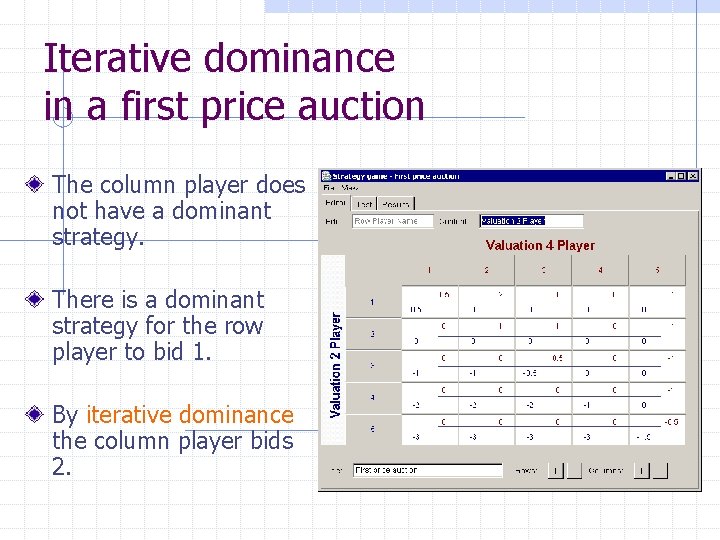
Dominance for the row player The column player does not have a dominant strategy. There is a dominant strategy for the row player to bid 1. By iterative dominance the column player bids 2.

Iterative dominance in a first price auction The column player does not have a dominant strategy. There is a dominant strategy for the row player to bid 1. By iterative dominance the column player bids 2.

Second price sealed bid auction In a second priced sealed bid auction, players simultaneously submit their bids, the highest bidder wins the auction, and pays the second highest bid. This is similar to Ebay, although Ebay is not sealed bid. For example, if the valuation 4 player bids 5 and the valuation 2 player bids 1, then the former wins the auction, pays 1 and makes a net profit of 3.

Dominance in a second price auction The row player has a dominant strategy of bidding 2. The column player has a dominant strategy of bidding 4. Thus both players have a dominant strategy of bidding their (known) valuation.

Comparing auction mechanisms Comparing the two auctions, the bidder place different bids but the outcome is the same, the column player paying 2 for the item. How robust is this result, that the form of the auction does not really matter? 1. Do people know their own valuations? 2. If not, are the valuations related? 3. What do bidders know about the valuations of their rivals? 4. Is everyone risk neutral? 5. How many items are up for sale, and how many units is each player bidding on? 6. Is collusion an issue?

Bidding strategies Recall that a strategy is a complete description of instructions to be played throughout the game, and that the strategic form of a game is the set of alternative strategies to each player and their corresponding expected payoffs from following them. Two games are strategically equivalent if they share the same strategic form. In strategically equivalent auctions, the set of bidding strategies that each potential bidders receive, and the mapping to the bidder’s payoffs, are the same.

Descending auctions are strategically equivalent to first-price auctions During the course of a descending auction no information is received by bidders. Each bidder sets his reservation price before the auction, and submits a market order to buy if and when the limit auctioneer's limit order to sell falls to that point. Dutch auctions and first price sealed bid auctions share strategic form, and hence yield the same realized payoffs if the initial valuation draws are the same. Rule 1: Pick the same reservation price in Dutch auction that you would submit in a first price auction

English auction In an English auction bidders compete against each other by successively raising the price at which they are willing to pay for the auctioned object. The bidding stops when nobody is willing to raise the price any further, and the item is sold to the person who has bid the highest price, at that price.

Second-price versus ascending auctions When there are only 2 bidders, an ascending auction mechanism is strategically equivalent to the second price sealed bid auction (because no information is received during the auction). More generally, both auctions are (almost) strategically equivalent if all bidders have independently distributed valuations (because the information conveyed by the other bidders has no effect on a bidder’s valuation). In common value auctions the 3 mechanisms are not strategically equivalent if there are more than 2 players. Rule 2: If there are only two bidders, or if valuations are independently distributed, choose the same reservation price in English, Japanese and second price auctions.

Bidding in a second-price auction If you know your own valuation, there is a general result about how to bid in a second price sealed bid auction, or where to stop bidding in an ascending auction. Bidding should not depend on what you know about the valuations of the other players, nor on what they know about their own valuations. It is a dominant strategy to bid your own valuation. A corollary of this result is that if every bidder knows his own valuation, then the object will be sold for the second highest valuation. Rule 3 : In a second price sealed bid auction, bid your valuation if you know it.

Proving the third rule Suppose you bid above your valuation, win the auction, and the second highest bid also exceeds your valuation. In this case you make a loss. If you had bid your valuation then you would not have won the auction in this case. In every other case your winnings would have been identical. Therefore bidding your valuation dominates bidding above it. Suppose you bid below your valuation, and the winning bidder places a bid between your bid and your valuation. If you had bid your valuation, you would have won the auction and profited. In every other case your winnings would have been identical. Therefore bidding your valuation dominates bidding below it. The proof is completed by combining the two parts.

Relaxing strategic equivalence In strategically equivalent auctions, the strategic form solution strategies of the bidders, and the payoffs to all them, are identical. This is a very strong form of equivalence. Can we show that such bidders might be indifferent to certain auctions which lack strategic equivalence?

Revenue equivalence defined The concept of revenue equivalence provides a useful tool for exploring this question. Two auction mechanisms are revenue equivalent if, given a set of players their valuations, and their information sets, the expected surplus to each bidder and the expected revenue to the auctioneer is the same. Revenue equivalence is a less stringent condition than strategic equivalence. Thus two strategic equivalent auctions are invariably revenue equivalent, but not all revenue equivalent auctions are strategic equivalent.

Preferences and Expected Payoffs Let: U(vn) denote the expected value of the nth bidder with valuation vn bidding according to his equilibrium strategy when everyone else does too. P(vn) denote the probability the nth bidder will win the auction when all players bid according to their equilibrium strategy. C(vn) denote the expected costs (including any fees to enter the auction, and payments in the case of submitting a winning bid).

An Additivity Assumption We suppose preferences are additive, symmetric and private, meaning: U(v) = P(v) v - C(v) So the expected value of participating in the auction is additive in the expected benefits of winning the auction and the expected costs incurred.

A revealed preference argument Suppose the valuation of n is vn and the valuation of j is vj. The surplus from n bidding as if his valuation is vj is U(vj), the value from participating if his valuation is vj, plus the difference in how he values the expected winnings compared to a bidder with valuation vj, or (vn – vj)P(vj). In equilibrium the value of n following his solution strategy is at least as profitable as deviating from it by pretending his valuation is vj. Therefore: U(vn) > U(vj) + (vn – vj)P(vj)

Revealed preference continued For convenience, we rewrite the last slide on the previous page as: U(vn) - U(vj) > (vn – vj)P(vj) Now viewing the problem from the jth bidder’s perspective we see that by symmetry: U(vj) > U(vn) + (vj – vn)P(vn) which can be expressed as: (vn– vj)P(vn) > U(vn) - U(vj)

A fundamental equality Putting the two inequalities together, we obtain: (vn – vj) P(vn)> U(vn) - U(vj) > (vn – vj) P(vj) Writing: vn = vj + dv yields: which, upon integration, yields:

Revenue equivalence This equality shows that in private value auctions, the expected surplus to each bidder does not depend on the auction mechanism itself providing two conditions are satisfied: 1. In equilibrium the auction rules award the bid to the bidder with highest valuation. 2. The expected value to the lowest possible valuation is the same (for example zero). Note that if all the bidders obtain the same expected surplus, the auctioneer must obtain the same expected revenue.

A theorem Assume each bidder: - is a risk-neutral demander for the auctioned object; - draws a valuation independently from a common, strictly increasing probability distribution function. Consider auction mechanisms where: - the buyer with the highest valuation always wins - the bidder with the lowest feasible signal expects zero surplus. Then the same expected revenue is generated by the

Steps for deriving expected revenue The expected revenue from any auction satisfying the conditions of theorem, is the expected value of the second highest bidder. To obtain this quantity, we proceed in two steps: of the 1. derive the probability distribution second highest valuation find 2. obtain its density and integrate to the mean.

Probability distribution of the second highest valuation Since any auction satisfying the conditions for theorem can be used to calculate the expected revenue, we select the second price auction. The probability that the second highest valuation is less than x is the sum of the probabilities that: 1. all the valuations are less than x, or: F(x)N 2. N-1 valuations are less than x and the other one is greater than x. There are N ways of doing this so the probability is: NF(x)N-1[1 - F(x)] The probability distribution for the second highest valuation is therefore: NF(x)N-1 - (N - 1) F(x)N

Expected revenue from Private Value Auctions The probability density function for the second highest valuation is therefore: N(N – 1)F(x)N-2 [1 - F(x)]F‘(x) Therefore the expected revenue to the auctioneer, or the expected value of the second highest valuation is:

Using the revenue equivalence theorem to derive optimal bidding functions We can also derive the solution bidding strategies for auctions that are revenue equivalent to the second price sealed bid auction. Consider, for example a first price sealed bid auctions with independent and identically distributed valuations. The revenue equivalence theorem implies that each bidder will bid the expected value of the next highest bidder conditional upon his valuation being the highest.

Bidding in a first price sealed bid auction The truncated probability distribution for the next highest valuation when vn is the highest valuation is: In a symmetric equilibrium to first price sealed bid auction, we can show that a bidder with valuation vn bids:

Comparison of bidding strategies The bidding strategies in the first and second price auctions markedly differ. In a second price auction bidders should submit their valuation regardless of the number of players bidding on the object. In the first price auction bidders should shave their valuations, by an amount depending on the number of bidders.

The derivation The probability of the remaining valuations being less than w when the highest valuation is v(1) is: Therefore the probability density for the second highest valuation when vn = v(1) is: This implies the expected value of the second highest valuation, conditional on vn = v(1) is: Integrating by parts we obtain the bidding function:

An example: the uniform distribution Suppose valuations are uniformly distributed within a closed interval, with probability distribution: Then in equilibrium, a player with valuation v bids a weighted average of the lowest possible valuation and his own, where the weights are 1/N and (N-1)/N:

When does revenue equivalence fail? The private valuations of bidders might be drawn from probability distributions that are not identical. The theorem does not apply when values are not private, such as when bidders receive signals about the value of the object to them that are correlated with each other. Bidders might be risk averse or risk loving rather than risk neutral. (This is of less importance value maximizing firms. )

Affiliated Valuations The revenue equivalence theorem applies to situations where the valuation of each is bidder is independently distributed. This is not always a valid assumption, because how a bidder values the object on the auction block for his own use might depend on information that another bidder has.

An example: Value of the object not known to bidders Consider a new oil field tract that drillers bid for after conducting seismic their individual explorations. The value of the oil field is the same to each bidder, but unknown. The nth bidder receives a signal sn which is distributed about the common value v, where sn = v + n and n E[v| sn] – v is independently distributed across bidders. Notice that each drilling company would have more precise estimates of the common valuation from reviewing the geological survey results of their rivals.

The expected value of the item upon winning the auction If the nth bidder wins the auction, he realizes his signal exceeded the signals of everybody else, that is sn ≡ max{s₁, …, s. N} so he should condition the expected value of the item on this new information. His expected value is now the expected value of vn conditional upon observing the maximum signal: E[vn| sn ≡ max{s₁, …, s. N}] This is the value that the bidder should use in the auction, because he should recognize that unless his signal is the maximum he will receive a payoff of zero.

The Winner’s Curse Conditional on the signal, but before the bidding starts, the expectation of the common value is We define the winner’s curse as Although bidders should take the winner's curse into account, there is widespread evidence that novice bidders do not take this extra information into account when placing a bid.

Symmetric valuations We relax independence and consider the class of symmetric valuations, which have two defining features: 1. All bidders have the same utility function. 2. Each bidder only cares about the collection of signals received by the other bidders, not who received them. Thus we may write the valuation of bidder n as:

Revenue Comparisons for Symmetric Auctions We can rank the expected revenue generated in symmetric equilibrium for auctions where valuations are also symmetric. There are two basic results. In a symmetric auction: 1. The expected revenue from a Japanese auction is higher than what an English auction yields. 2. The expected revenue from an English auction exceeds a first price sealed bid auction.

Asymmetric valuations In a private valuation auctions suppose the bidders have different uses for the auctioned object, and this fact is common knowledge to every bidder. Each bidder knows the probability distributions from which the other valuations are drawn, and uses that information when making her bid. In that case the revenue equivalence theorem is not valid, and the auctioneer's prefers some types of auctions over others. What happens if the private valuations of bidders are not drawn from the same probability distribution function?

An example of asymmetry Instead of assuming all bidders appear the same to the seller and to each other, suppose that bidders fall into two recognizably different classes. Suppose there are two cumulative distributions, F₁(v) and F₂(v) with probability p₁ and p₂ respectively. Thus: F(v) = p₁F₁(v) + p₂F₂(v) Bidders of type i ∈ {1, 2} draw their valuations independently from the distribution Fi(v). We assume the supports are continuous and overlap, but that they do not coincide.

An example of asymmetry Instead of assuming all bidders appear the same to the seller and to each other, suppose that bidders fall into two recognizably different classes. Suppose there are two cumulative distributions, F₁(v) and F₂(v) with probability p₁ and p₂ respectively. Thus: F(v) = p₁F₁(v) + p₂F₂(v) Bidders of type i ∈ {1, 2} draw their valuations independently from the distribution Fi(v). We assume the supports are continuous and overlap, but that they do not coincide.

A conceptual experiment Suppose each bidder sees his valuation, but does not immediately learn whether other bidders comes from the high or low probability distribution. At that point the bidding strategy cannot depend on which probability distribution the other valuations come from. She forms her bid b(v). Then each bidder is told what type of person the other bidders are, type i ∈ {1, 2}, that is whether their valuations were drawn from F₁(v) and F₂(v). How should she revise her bid?

Intuition Suppose F₁(v) and F 2(v) have the same support, but F 1(v) first order stochastically dominates F 2(v), that is F₁(v) 6 F 2(v). When a bidder learns that his valuation is drawn from F 2(v) (respectively F₁(v)), he deduces the other one is more likely to draw a higher (lower) valuation than himself, realizes the probability of winning falls (rises), so adjusts his bid upwards (downwards). The intuition is in first price auctions to bid aggressively from weakness and vice versa.

Bidding with differential information Another type of asymmetry occurs when one bidder knows more about the value of the object being auctioned than the others. What happens if they are asymmetrically informed about a common value? An extreme form of dependent signals occurs when one bidder know the signal and the others do not. How should an informed player bid? What about an uninformed player?

Second price sealed bid auctions The arguments we have given in previous lectures imply the informed player optimally bids the true value. The uninformed player bids any pure or mixed distribution. If he wins the auction he pays the common value, if he loses he pays nothing, and therefore makes neither gains or losses on any bid. This implies the revenue from the auction is indeterminate.

Perspective of the less informed bidder in a first price auction Suppose the uninformed bidder always makes the same positive bid, denoted b. This is an example of a pure strategy. Is this pure strategy part of a Nash equilibrium? The best response of the informed bidder is to bid a little more than b when the value of the object v is worth more than b, and less than b otherwise. Therefore the uninformed bidder makes an expected loss by playing a pure strategy in this auction. A better strategy would be to bid nothing.

A theorem on first price sealed bid auctions The argument in the previous slide shows that the uninformed bidder plays a mixed strategy in this game. One can show that when the auctioned item is worth v the informed bidder bids: (v) = E[V|V v] in equilibrium, and that the uninformed bidder chooses a bid at random from the interval [0, E[V]] according to the probability distribution H defined by H(b) = Prob[ (v) b]

Return to the uninformed bidder If the uninformed player bids more than E[V], then his expected return is negative, since he would win the auction every time v < E[V] but less frequently when v > E[V]. We now show that if his bid b < E[V], his expected return is zero, and therefore any bid b < E[V] is a best response to the informed player’s bid. If the uniformed bids less than E[V] and loses the auction, his return is zero. If he bids less than E[V] and wins the auction, his return is E[V| (V) < b] – b = E[V| V < -1(b) ] – b = ( -1(b) ) – b = 0

Return to the informed bidder Since the uninformed player bids less than E[v] with unit probability, so does the informed player. Noting that (w) varies from v to E[v], we prove it is better to bid (v) rather than (w). Given a valuation of v, the expected net benefit from bidding (w) is: H( (w))[v - (w)] = Pr{V w}[v - (w)] = F(w)[v - (w)] Differentiating with respect to w, using derivations found on the next slide, yields F’(w)[v - w] which is positive for all v > w and negative for all v < w, and zero at v = w. Therefore bidding (v) is optimal for the informed bidder with valuation v.

The derivative Noting it follows from the fundamental theorem of calculus that and so the derivative of F(w)[v - (w)] with respect to w is :

Lecture Summary We described several types of auction mechanisms. We showed conditions under which auctions are strategically equivalent, revenue equivalent, and compared revenue from different auctions when these conditions do not hold. We showed how to derive the optimal bidding rule for several private value auctions, and explained the nature of the winner’s curse in common value auctions.