Lecture 7 A Tale of Two Graphs and

Lecture 7: A Tale of Two Graphs (and a tree) CS 201 J: Engineering Software University of Virginia 23 September 2003 Computer Science CS 201 J Fall 2003 David Evans http: //www. cs. virginia. edu/evans

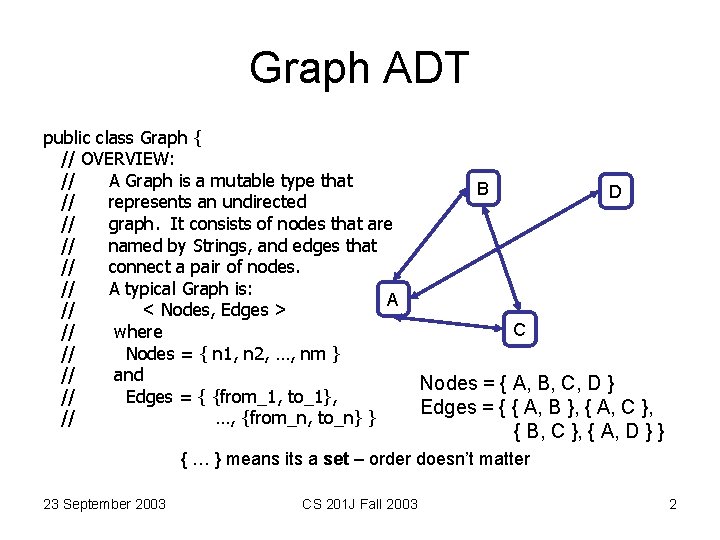
Graph ADT public class Graph { // OVERVIEW: // A Graph is a mutable type that // represents an undirected // graph. It consists of nodes that are // named by Strings, and edges that // connect a pair of nodes. // A typical Graph is: A // < Nodes, Edges > // where // Nodes = { n 1, n 2, …, nm } // and // Edges = { {from_1, to_1}, // …, {from_n, to_n} } B D C Nodes = { A, B, C, D } Edges = { { A, B }, { A, C }, { B, C }, { A, D } } { … } means its a set – order doesn’t matter 23 September 2003 CS 201 J Fall 2003 2

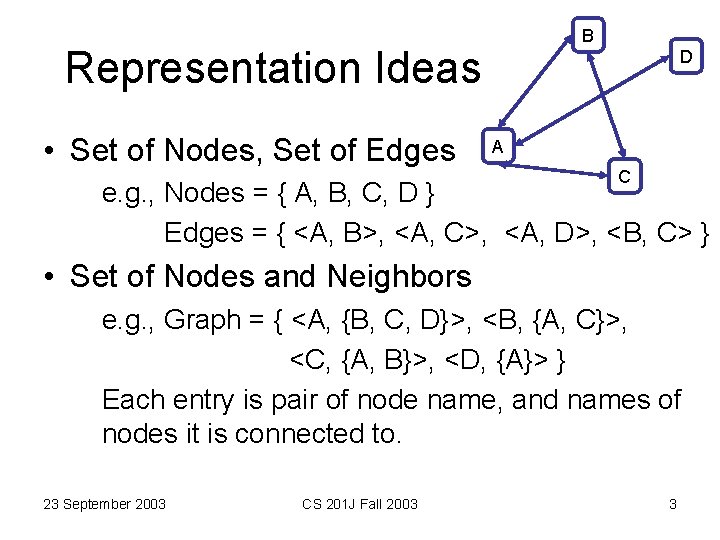
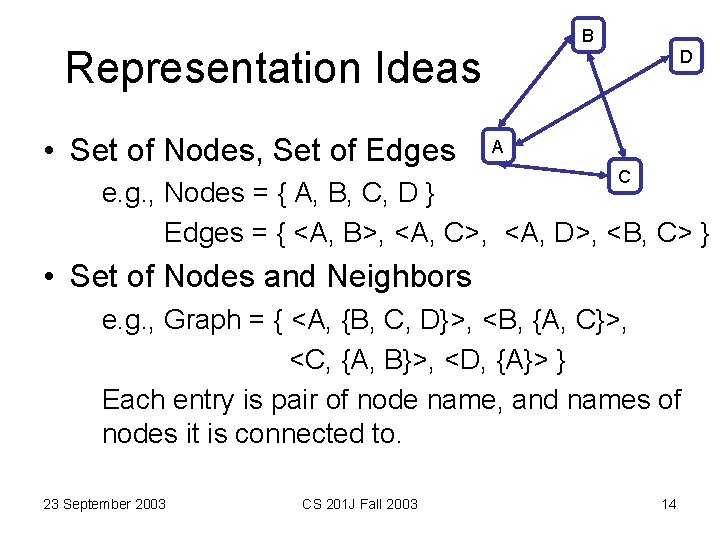
B Representation Ideas • Set of Nodes, Set of Edges D A C e. g. , Nodes = { A, B, C, D } Edges = { <A, B>, <A, C>, <A, D>, <B, C> } • Set of Nodes and Neighbors e. g. , Graph = { <A, {B, C, D}>, <B, {A, C}>, <C, {A, B}>, <D, {A}> } Each entry is pair of node name, and names of nodes it is connected to. 23 September 2003 CS 201 J Fall 2003 3

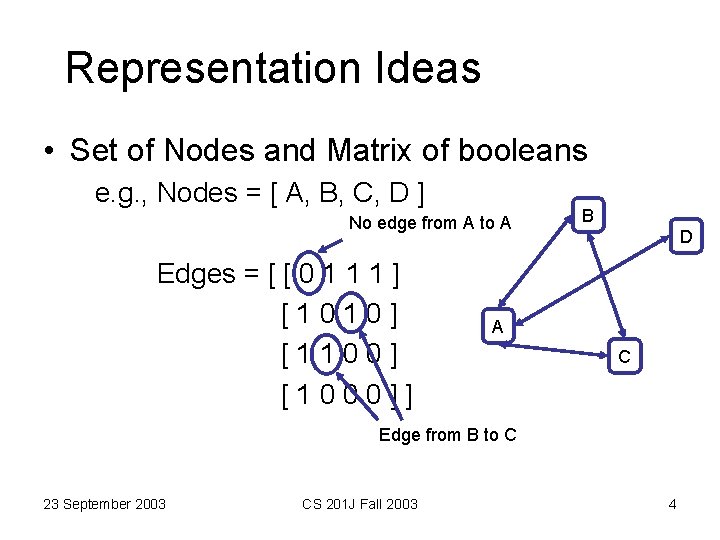
Representation Ideas • Set of Nodes and Matrix of booleans e. g. , Nodes = [ A, B, C, D ] No edge from A to A Edges = [ [ 0 1 1 1 ] [1010] [1100] [1000]] B D A C Edge from B to C 23 September 2003 CS 201 J Fall 2003 4

Implementation 1 class Edge { // OVERVIEW: Record type for representing an edge. String node 1, node 2; Edge (String n 1, String n 2) { node 1 = n 1; node 2 = n 2; } } class Graph { // OVERVIEW: A Graph is a mutable type that represents an … Vector nodes; // A Vector of String objects Vector edges; // A Vector of Edge object } … 23 September 2003 CS 201 J Fall 2003 5

Rep Invariant Function from rep to boolean class Edge { String node 1, node 2; } class Graph { Vector nodes; // A Vector of String objects Vector edges; // A Vector of Edge object …} RI (c) = c. nodes != null && c. edges != null && !c. nodes. contains. Null && !c. edges. contains. Null && elements of c. nodes are String objects && elements of c. edges are Edge objects && no duplicates in c. nodes && no duplicates in c. edges Is this precise enough? && every node mentioned in c. edges is also in c. nodes 23 September 2003 CS 201 J Fall 2003 6

Rep Invariant RI (c) = && && && c. nodes != null && c. edges != null !c. nodes. contains. Null && !c. edges. contains. Null elements of c. nodes are String objects elements of c. edges are Edge objects && no duplicates in c. nodes // No duplicate edges, node 1/node 2 are interchangable: && ((c. edges[i]. node 1 = c. edges[j]. node 1 && c. edges[i]. node 2 = c. edges[j]. node 2) || (c. edges[i]. node 1 = c. edges[j]. node 2 && c. edges[i]. node 2 = c. edges[j]. node 1)) i == j && every node mentioned in c. edges is also in c. nodes 23 September 2003 CS 201 J Fall 2003 7

Abstraction Function public class Graph { // OVERVIEW: // A Graph is a mutable type that // represents an undirected // graph. It consists of nodes that are // named by Strings, and edges that // connect a pair of nodes. // A typical Graph is: // < Nodes, Edges > // where // Nodes = { n 1, n 2, …, nm } // and // Edges = { {from_1, to_1}, // …, {from_n, to_n} } 23 September 2003 • Function from rep to abstract notion (use notation from overview) AF (c) = < Nodes, Edges > where … CS 201 J Fall 2003 8

Abstraction Function class Edge { String node 1, node 2; } class Graph { Vector nodes; // A Vector of String objects Vector edges; // A Vector of Edge object …} AF (c) = < Nodes, Edges > where Nodes = { c. nodes[i] | 0 <= i < c. nodes. size () } The set of nodes is the elements of the c. nodes Vector Edges = { { c. edges[i]. node 1, c. edges[i]. node 2 } | 0 <= i < c. edges. size () } The set of edges is the elements of the c. edges Vector 23 September 2003 CS 201 J Fall 2003 9

class Edge { String node 1, node 2; } Implementing Constructor class Graph { Vector nodes; // A Vector of String objects Vector edges; // A Vector of Edge object …} public Graph () // EFFECTS: Initializes this to a graph with no nodes or // } edges: < {}, {} >. nodes = new Vector (); edges = new Vector (); 23 September 2003 How do we know this satisfies the rep invariant? CS 201 J Fall 2003 10

Implementing add. Node class Edge { String node 1, node 2; } class Graph { Vector nodes; // A Vector of String objects Vector edges; // A Vector of Edge object …} public void add. Node (String name) { // REQUIRES: name is not the name of a node in this // MODIFIES: this // EFFECTS: adds a node named name to this: // } this_post = < this_pre. nodes U { name }, this_pre. edges > nodes. add. Element (name); 23 September 2003 How do we know this still satisfies the rep invariant? CS 201 J Fall 2003 11

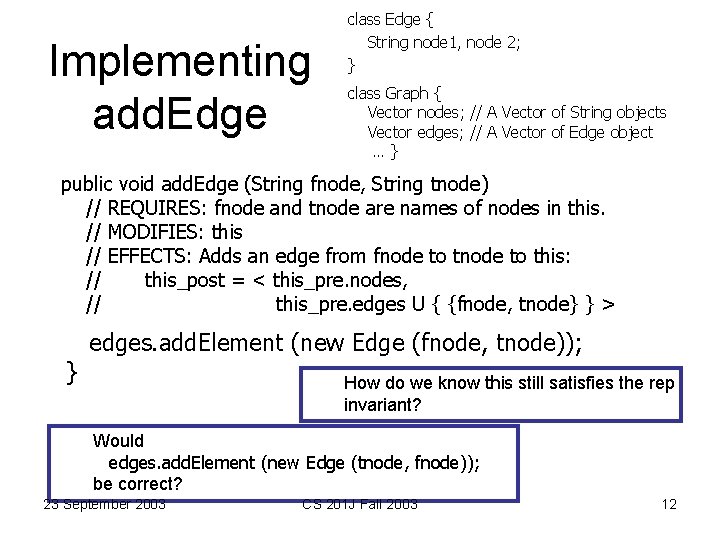
Implementing add. Edge class Edge { String node 1, node 2; } class Graph { Vector nodes; // A Vector of String objects Vector edges; // A Vector of Edge object …} public void add. Edge (String fnode, String tnode) // REQUIRES: fnode and tnode are names of nodes in this. // MODIFIES: this // EFFECTS: Adds an edge from fnode to this: // this_post = < this_pre. nodes, // this_pre. edges U { {fnode, tnode} } > } edges. add. Element (new Edge (fnode, tnode)); How do we know this still satisfies the rep invariant? Would edges. add. Element (new Edge (tnode, fnode)); be correct? 23 September 2003 CS 201 J Fall 2003 12

Implementing get. Neighbors class Edge { String node 1, node 2; } class Graph { Vector nodes; // A Vector of String objects Vector edges; // A Vector of Edge object …} public String. Set get. Neighbors (String node) // REQUIRES: node is a node in this // EFFECTS: Returns the String. Set consisting of all nodes in this // that are directly connected to node: // result = { n | {node, n} is in this. edges } String. Set res = new String. Set (); Enumeration edgeenum = edges. elements (); while (edgeenum. has. More. Elements ()) { Edge e = (Edge) edgeenum. next. Element (); if (e. node 1. equals (node)) { res. insert (e. node 2); } else if (e. node 2. equals (node)) { res. insert (e. node 1); } 23 September 2003 CS 201 J Fall 2003 13

B Representation Ideas • Set of Nodes, Set of Edges D A C e. g. , Nodes = { A, B, C, D } Edges = { <A, B>, <A, C>, <A, D>, <B, C> } • Set of Nodes and Neighbors e. g. , Graph = { <A, {B, C, D}>, <B, {A, C}>, <C, {A, B}>, <D, {A}> } Each entry is pair of node name, and names of nodes it is connected to. 23 September 2003 CS 201 J Fall 2003 14

Implementation 2 class Node. Neighbors { // OVERVIEW: Record type for representing an edge. String node; String. Set neighbors; // A Set of String objects Node. Neighbors (String n) { node = n; neighbors = new String. Set (); } } class Graph { // OVERVIEW: A Graph is a mutable type that represents an … Vector nodes; // A Vector of Node. Neighbors objects … } 23 September 2003 CS 201 J Fall 2003 15

Rep Invariant Function from rep to boolean class Node. Neighbors { String node; String. Set neighbors; } class Graph { Vector nodes; // A Vector of Node. Neighbors objects } RI (c) = c. nodes != null && !c. nodes. contains. Null && elements of c. nodes are Node. Neighbors objects && no duplicates in c. nodes && for each node in c. nodes, each node in c. nodes[i]. neighbors is a node in c. nodes[i]. neighbors does not contain duplicates 23 September 2003 CS 201 J Fall 2003 16

Abstraction Function class Node. Neighbors { String node; String. Set neighbors; } class Graph { Vector nodes; // A Vector of Node. Neighbors objects } AF (c) = < Nodes, Edges > where Nodes = { c. nodes[i]. node | 0 <= i < c. nodes. size () } The set of nodes is the elements of the c. nodes Vector Edges = { { c. nodes[i]. node, c. nodes[i]. neighbors[e] } | 0 <= i < c. nodes. size (), 0 <= e <= c. nodes[i]. neighbors. size () } 23 September 2003 CS 201 J Fall 2003 17

Implementing Constructor class Node. Neighbors { String node; Vector neighbors; // A Vector of String objects } class Graph { Vector nodes; // A Vector of Node. Neighbors objects } public Graph () // EFFECTS: Initializes this to a graph with no nodes or // } edges: < {}, {} >. nodes = new Vector (); 23 September 2003 CS 201 J Fall 2003 18

Implementing add. Node class Node. Neighbors { String node; String. Set neighbors; } class Graph { Vector nodes; // A Vector of Node. Neighbors objects } public void add. Node (String name) { // REQUIRES: name is not the name of a node in this // MODIFIES: this // EFFECTS: adds a node named name to this: // } this_post = < this_pre. nodes U { name }, this_pre. edges > nodes. add. Element (new Node. Neighbors (name)); How do we know this still satisfies the rep invariant? 23 September 2003 CS 201 J Fall 2003 19

Implementing add. Edge class Node. Neighbors { String node; String. Set neighbors; } class Graph { Vector nodes; // A Vector of Node. Neighbors objects } public void add. Edge (String fnode, String tnode) // REQUIRES: fnode and tnode are names of nodes in this. // MODIFIES: this // EFFECTS: Adds an edge from fnode to this: // this_post = < this_pre. nodes, // this_pre. edges U { {fnode, tnode} } > } Node. Neighbors n 1 = lookup. Node (fnode); Node. Neighbors n 2 = lookup. Node (tnode); n 1. neighbors. insert (tnode); n 2. neighbors. insert (fnode); 23 September 2003 We need to implement lookup. Node also. How do we know this still satisfies the rep invariant? CS 201 J Fall 2003 20

Implementing get. Neighbors class Node. Neighbors { String node; String. Set neighbors; } class Graph { Vector nodes; // A Vector of Node. Neighbors objects } public String. Set get. Neighbors (String node) // REQUIRES: node is a node in this // EFFECTS: Returns the String. Set consisting of all nodes in this // that are directly connected to node: // result = { n | {node, n} is in this. edges } Node. Neighbors n = lookup. Node (node); return n. neighbors; Almost…but we have exposed our rep! 23 September 2003 CS 201 J Fall 2003 21

Rep Exposure What if client does this? Graph g = new Graph (); g. add. Node (“A”); g. add. Node (“B”); g. add. Edge (“A”, “B”); String. Set neighbors = g. get. Neighbors (“A”); neighbors. insert (“C”); Does the rep invariant for g still hold? 23 September 2003 CS 201 J Fall 2003 22

Rep Exposure • If mutable components of the representation are accessible to clients, the implementation exposes the rep! • Clients can mutate the representation directly – without using data type operations Why is this bad? 23 September 2003 CS 201 J Fall 2003 23

Problems with Rep Exposure • Client mutations could break the rep invariant • Client code may break if ADT implementation changes • No longer possible to reason about the invariant being true by just checking the ADT implementation 23 September 2003 CS 201 J Fall 2003 24

Implementing get. Neighbors class Node. Neighbors { String node; String. Set neighbors; } class Graph { Vector nodes; // A Vector of Node. Neighbors objects } public String. Set get. Neighbors (String node) // REQUIRES: node is a node in this // EFFECTS: Returns the String. Set consisting of all nodes in this // that are directly connected to node: // result = { n | {node, n} is in this. edges Node. Neighbors n = lookup. Node (node); n. neighbors; return n. neighbors. copy (); } 23 September 2003 If we return a copy, the client doesn’t have access to the actual neighbors object in the representation. CS 201 J Fall 2003 25

Which implementation is better? • Depends what we care about • Code complexity – Normally the most important criteria – Nodes/Edges: get. Neighbors is harder – Node. Neighbors: to. String is harder, add. Edge a little harder • Memory Use – Nodes/Edges: 2 vectors, each edge requires 2 strings – Node. Neighbors: 1 vector, number of nodes String. Sets, each edge requires 1 string 23 September 2003 CS 201 J Fall 2003 26

Which implementation is better? • Performance – Both have poor performance: linear search through all the nodes to find one – Node. Neighbors get. Neighbors does less work – Other methods Nodes/Edges usually less work – If we expect clients to call get. Neighbors a lot, Node. Neighbors might be better 23 September 2003 CS 201 J Fall 2003 27

Performance Comparison > time java Graph. Test // Using Nodes/Edges impl 1. 220 u 0. 020 s 0: 01. 25 99. 2% > time java Graph. Test // Using Node. Neighbors impl 0. 660 u 0. 040 s 0: 00. 79 88. 6% Very rough comparison…but Node. Neighbors appears to be twice as fast for this test case. What is the test case doing? 23 September 2003 CS 201 J Fall 2003 28

Graph. Test. java public class Graph. Test { static public void main (String args[]) { Graph g = new Graph (); int numnodes = 1000; } } for (int i = 0; i < numnodes; i++) { g. add. Node ("node" + i); } for (int i = 0; i < numnodes - 1; i++) { g. add. Edge ("node" + i, "node" + (i + 1)); } for (int i = 0; i < numnodes - 2; i++) { g. add. Edge ("node" + i, "node" + (i + 2)); } for (int i = 0; i < numnodes; i++) { String. Set neighbors = g. get. Neighbors ("node" + i); } 23 September 2003 CS 201 J Fall 2003 29

Charge When picking representations, focus on complexity of implementation Your time is (usually) more valuable than the computer’s! 23 September 2003 CS 201 J Fall 2003 30