Lecture 7 1 Electric Potential Energy of a

Lecture 7 -1 Electric Potential Energy of a Charge (continued) 0 i is “the” reference point. Choice of reference point (or point of zero potential energy) is arbitrary. i is often chosen to be infinitely far ( )

Lecture 7 -2 Electric Potential • U(r) of a test charge q 0 in electric field generated by other source charges is proportional to q 0. • So U(r)/q 0 is independent of q 0, allowing us to introduce electric potential V independent of q 0. taking the same reference point • [Electric potential] = [energy]/[charge] SI units: J/C = V (volts) Scalar! Potential energy difference when 1 C of charge is moved between points of potential difference 1 V

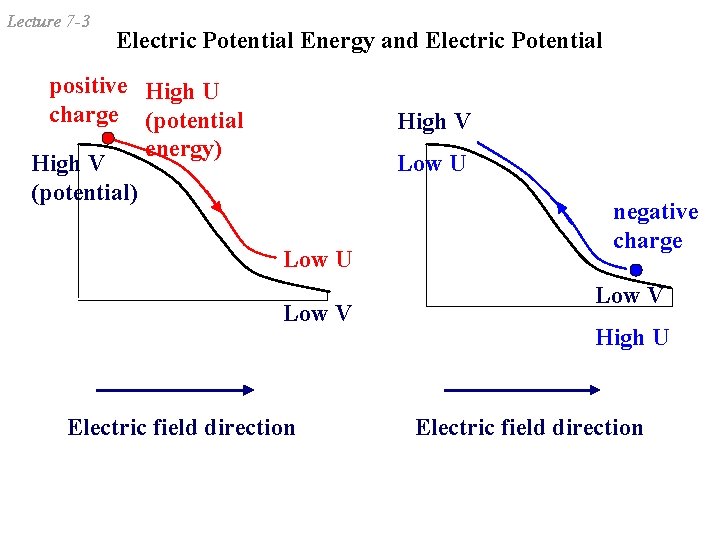
Lecture 7 -3 Electric Potential Energy and Electric Potential positive High U charge (potential energy) High V (potential) High V Low U Low V Electric field direction negative charge Low V High U Electric field direction

Lecture 7 -4 E from V We can obtain the electric field E from the potential V by inverting the integral that computes V from E: Expressed as a vector, E is the negative gradient of V E always points from high V to low V. (But high V is high U only for a positive charge. )

Lecture 7 -5 READING QUIZ 1 A conducting sphere A with radius RA = 1 meter is connected via a conducting wire to a conducting sphere B with radius RB = ½ meter. The spheres have a total charge Q = QA + QB. The radial electric fields at surface of the spheres are EA and EB respectively. Which of the following statements is correct? A| EA > EB B| EA = EB C| EA = 1/2 EB D| EA = 2 EB

Lecture 7 -6 Equipotential Surfaces • An equipotential surface is a surface on which the potential is the same everywhere. For a displacement Δr of a test charge q 0 along an equipotentital, U = constant on an equipotential surface. E is everywhere perpendictular to U Potential difference between nearby equipotentials is approximately equal to E times the separation distance. Equipotential surfaces are drawn at constant intervals of ΔV http: //www. its. caltech. edu/~phys 1/java/phys 1/EField. html

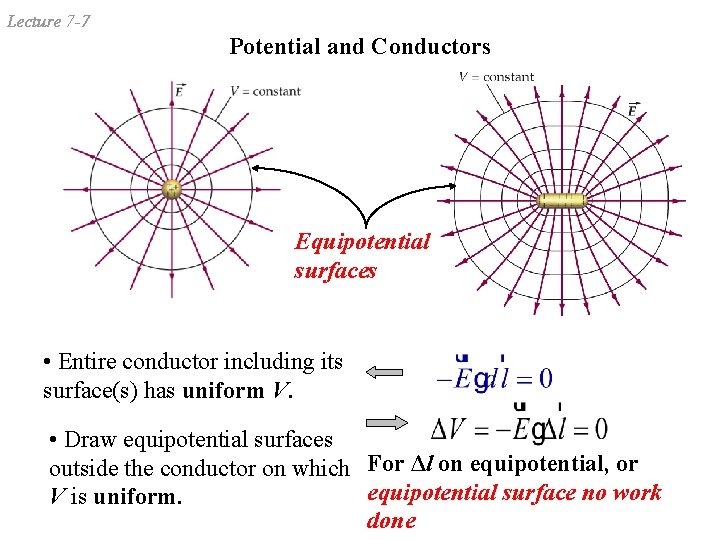
Lecture 7 -7 Potential and Conductors Equipotential surfaces • Entire conductor including its surface(s) has uniform V. • Draw equipotential surfaces outside the conductor on which For Δl on equipotential, or equipotential surface no work V is uniform. done

Lecture 7 -8 Potential of a Uniformly Charged Sheet Electric field is uniform on each side of the sheet as shown. Equipotential surfaces are perpendictular to the electric fields. Separation between equipotential surfaces are equal to the potential differences divided by the magnitude of electric field.

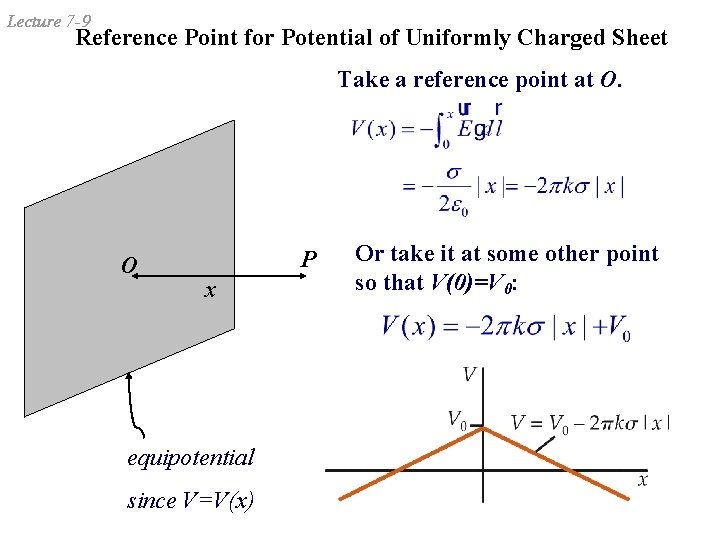
Lecture 7 -9 Reference Point for Potential of Uniformly Charged Sheet Take a reference point at O. O P x equipotential since V=V(x) Or take it at some other point so that V(0)=V 0:

Lecture 7 -10 Two Ways to Calculate Potential • Integrate -E from the reference point at (∞) to the point (P) of observation: Q r P Ø A line integral (which could be tricky to do) Ø If E is known and simple and a simple path can be used, it may be reduced to a simple, ordinary 1 D integral. • Integrate d. V (contribution to V(r) from each infinitesimal source charge dq) over all source charges: q 1 q 3 P q 2 Q P q 4

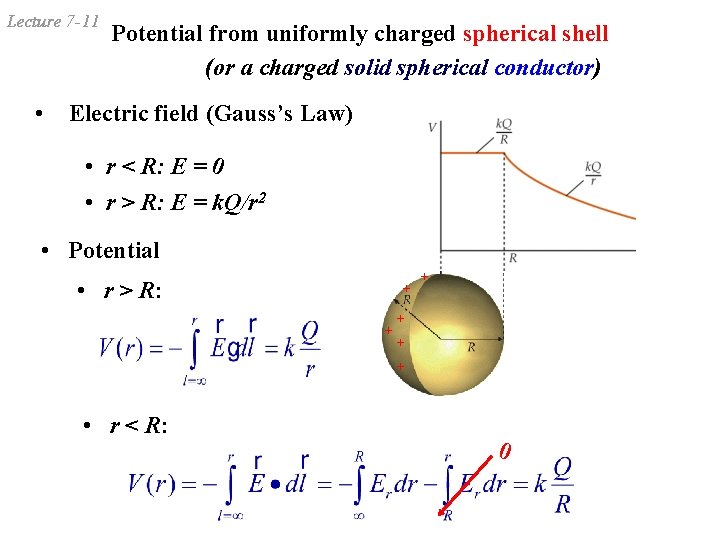
Lecture 7 -11 • Potential from uniformly charged spherical shell (or a charged solid spherical conductor) Electric field (Gauss’s Law) • r < R: E = 0 • r > R: E = k. Q/r 2 • Potential • r > R: + + + • r < R: 0

Lecture 7 -12 D 0 CCAM 2

Lecture 7 -13

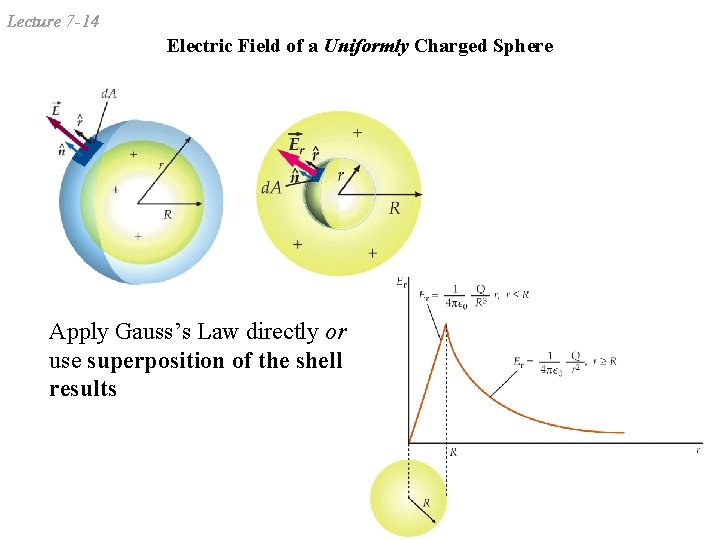
Lecture 7 -14 Electric Field of a Uniformly Charged Sphere Apply Gauss’s Law directly or use superposition of the shell results

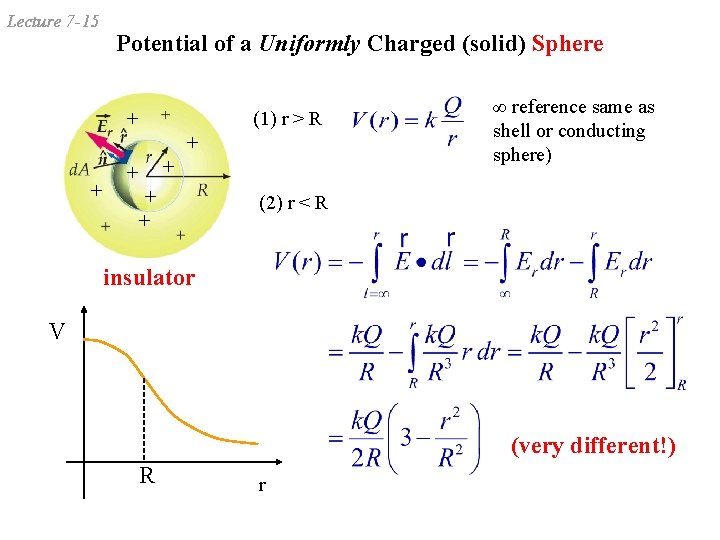
Lecture 7 -15 Potential of a Uniformly Charged (solid) Sphere + (1) r > R + + + ∞ reference same as shell or conducting sphere) (2) r < R insulator V (very different!) R r

Lecture 7 -16 Physics 241 –warm-up Quiz 2 A infinite plane with uniform charge density +σ. What is the potential difference VB-VA? a) b) c) d) e) -(3/2)σ/ε 0 -σ/2ε 0 3σ/ε 0 σ/2ε 0 -3σ/ε 0 +σ. A B 1 m 2 m

Lecture 7 -17 Charged Concentric Spherical Conductors V (a) r > c (b) b < r < c r Qout Qin c (c) a < r < b b a (d) r < a

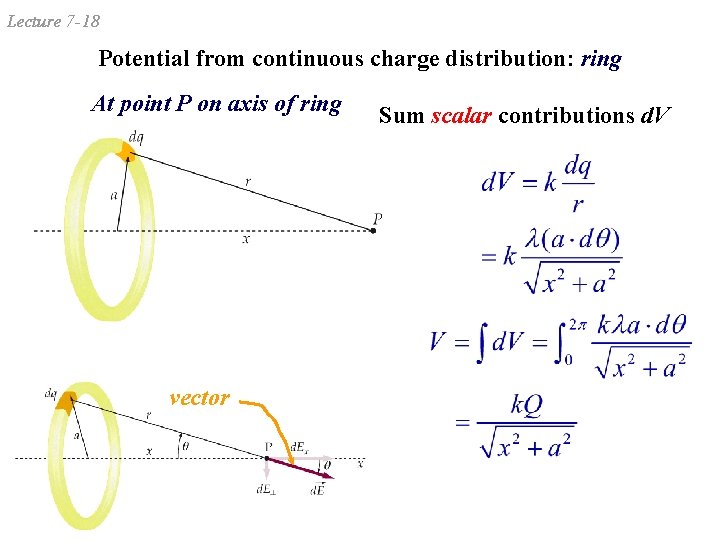
Lecture 7 -18 Potential from continuous charge distribution: ring At point P on axis of ring vector Sum scalar contributions d. V

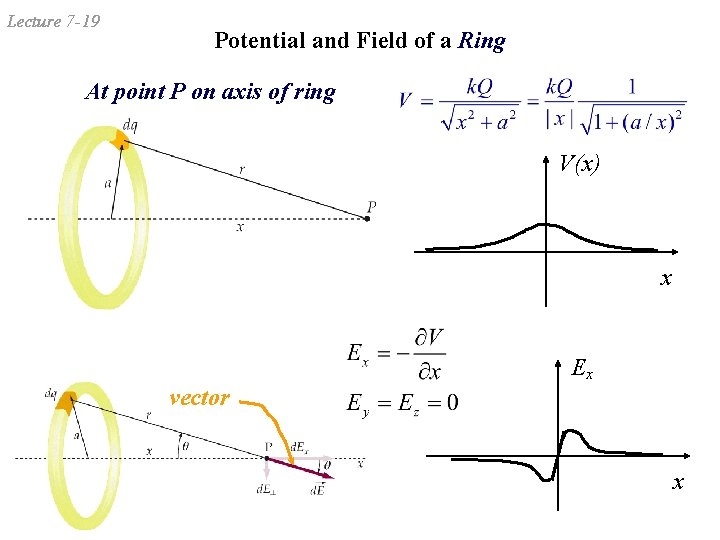
Lecture 7 -19 Potential and Field of a Ring At point P on axis of ring V(x) x Ex vector x

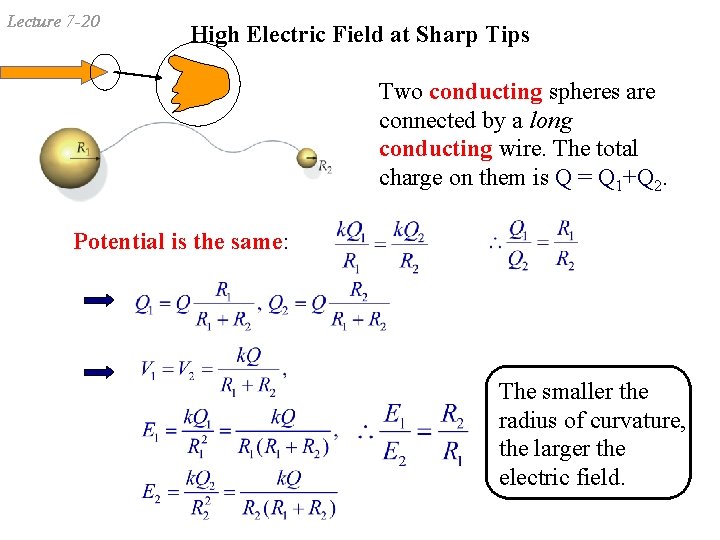
Lecture 7 -20 High Electric Field at Sharp Tips Two conducting spheres are connected by a long conducting wire. The total charge on them is Q = Q 1+Q 2. Potential is the same: The smaller the radius of curvature, the larger the electric field.

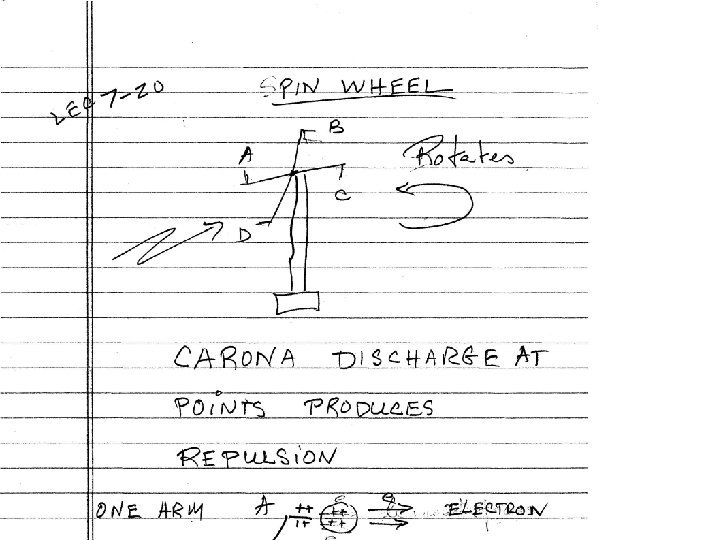
Lecture 7 -21 DOCCAM 2

Lecture 7 -22

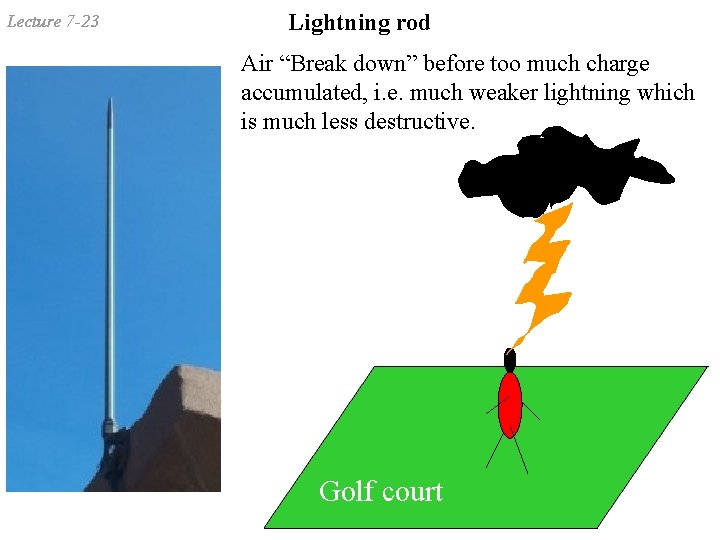
Lecture 7 -23 Lightning rod Air “Break down” before too much charge accumulated, i. e. much weaker lightning which is much less destructive. Golf court

Lecture 7 -24 Physics 241 10: 30 Quiz 3 A spherical shell of radius 50 cm is charged uniformly with a total charge of Q Coulombs. What is the potential difference VB-VA ? a) b) c) d) e) k. Q/2 -2 k. Q -(3/2)k. Q -k. Q/2 Q A B 1 m 2 m

Lecture 7 -25 Physics 241 11: 30 Quiz 3 Two parallel planes, 2 m apart, are charged with uniform charge densities 2σ and -σ (in C/m 2). Respectively as shown. What is the potential difference VB-VA (in volts)? a) b) c) d) e) -(3/2)σ/ε 0 -2σ/ε 0 3σ/ε 0 -3σ/ε 0 2 m A B

Lecture 7 -26 Physics 241 –Quiz 5 c A spherical shell of radius 20 cm is charged uniformly with a total charge of Q Coulombs. What is the potential difference VB-VA? a) b) c) d) e) k. Q/2 -2 k. Q -(3/2)k. Q -k. Q/2 Q A B 1 m 2 m