Lecture 6 Types of Types It would appear

Lecture 6: Types of Types “It would appear that we have reached the limits of what it is possible to achieve with computer technology, although one should be careful with such statements, as they tend to sound pretty silly in five years. ” John Von Neumann, 1949 CS 655: Programming Languages David Evans University of Virginia Computer Science 1 Feb 2000 University of Virginia CShttp: //www. cs. virginia. edu/~evans 655

Menu • • • PS 1 Results (John) Latent Types, Dynamic Checking Algol 60 Group Report Manifest Types, Dynamic Checking Manifest Types, Static Checking 1 Feb 2000 University of Virginia CS 655 2

Types integers in [0, …) Strings Beatle’s Song Titles Colors secret information programs that halt pointers that points to integer that is prime number pointers that points to pointer that points to storage shared by some other pointer • Type is any set of values • Next week’s definition will be different 1 Feb 2000 University of Virginia CS 655 3

Why have types? • Overloading operators + vs. FADD – compiler needs types to figure out what “+” means • Detecting program errors – Better to notice error than report incorrect result • Make programs easier to read, understand maintain – Better than comments if they are checked and can be trusted • Security – Can use types to constrain the behavior of programs (we’ll see Proof-Carrying Code later…) 1 Feb 2000 University of Virginia CS 655 4

Taxonomy • Latent vs. Manifest – Are types visible in the program text? • Checked statically vs. checked dynamically – Do you have to run the program to know if it has type errors? • Checked weakly vs. strongly – How strict are the rules for using types? • All combinations are (theoretically) possible – Language that is manifest + static + weak? – Language that is latent + dynamic + strong? 1 Feb 2000 University of Virginia CS 655 5

Labrador: BARK with Latent Types Instruction : : = STORE Loc Literal | HALT | ERROR (Same as BARK) | ADD Loc 1 Loc 2 Loc 1 gets the value of Loc 1 + Loc 2. Loc 1 and Loc 2 must be the same type, result has same type. | MUL Loc 1 Loc 2 Loc 1 gets the value of Loc 1 * Loc 2. Loc 1 and Loc 2 must be the same type. | IF Loc 1 THEN Loc 1 If value in Loc 1 is non-zero, jump to instruction corresponding to value in Loc 2. Loc 1 and Loc 2 must contain integers. Literal : : = Int. Literal | Real. Literal Int. Literal : : = [-]? [0 -9]* Has type integer. Real. Literal : : = [-]? [0 -9]* Has type real. As companions Labradors are kindly, patient, intelligent and always keen to please. They make perfect family dogs being especially good with children. Walter & Shackles Guide to Dogs 1 Feb 2000 University of Virginia CS 655 6

Labrador Program [0] STORE R 0 3. 14159 [1] STORE R 1 4. [2] MUL R 1 [3] MUL R 0 R 1 1 Feb 2000 University of Virginia CS 655 7

Operational Semantics: ADD BARK rule: Instructions[PC] = ADD Loc 1 Loc 2 < Instructions x PC x Register. File > < Instructions x PC’ x Register. File’ > where PC’ = PC + 1 Register. File’[n] = Register. File[n] Register. File’[n] = Register. File[Loc 1] + Register. File[Loc 2] if n Loc 1 What does this mean? 1 Feb 2000 University of Virginia CS 655 8

Typed Register File C = Instructions x PC x Register. File[i] = <type, value> for all integers i type = integer | real value = an integer if type if integer, a real if type is real Assume functions typeof(Register. File[i]), valueof(Register. File[i]) 1 Feb 2000 University of Virginia CS 655 9

Operational Semantics: ADDinteger Instructions[PC] = ADD Loc 1 Loc 2, typeof(Register. File[Loc 1]) = integer, typeof(Register. File[Loc 2]) = integer < Instructions x PC x Register. File > < Instructions x PC’ x Register. File’ > where PC’ = PC + 1 Register. File’[n] = Register. File[n] Register. File’[n] = if n Loc 1 <integer, valueof(Register. File[Loc 1]) +integer valueof(Register. File[Loc 2])> 1 Feb 2000 University of Virginia CS 655 10

Operational Semantics: ADDreal Instructions[PC] = ADD Loc 1 Loc 2, typeof(Register. File[Loc 1]) = real, typeof(Register. File[Loc 2]) = real < Instructions x PC x Register. File > < Instructions x PC’ x Register. File’ > where PC’ = PC + 1 Register. File’[n] = Register. File[n] Register. File’[n] = <real, valueof(Register. File[Loc 1]) +real valueof(Register. File[Loc 2])> 1 Feb 2000 University of Virginia CS 655 if n Loc 1 11

Strong vs. Weak Typing • What do we have? – Latent, dynamic, strongly typed language • To get: latent, dynamic, weakly typed language: – Allow ADD and MUL to work on mixed types, result is real, allow IF predicate to be real – Add transition rules for Instructions[PC] = ADD Loc 1 Loc 2, typeof(Register. File[Loc 1]) = real, typeof(Register. File[Loc 2]) = integer etc. 1 Feb 2000 University of Virginia CS 655 12

Is Dynamic Type Checking Useful? 1 Feb 2000 University of Virginia CS 655 13

Manifest Types Often, however, explicit (manifest) types make programs easier for compilers to read, not easier for humans to read; and explicit (manifest) types are generally cumbersome for the program writer as well. Implicitly (latently) typed programming languages thus have clear advantages in terms of readability and writability. Turbak & Gifford 1 Feb 2000 University of Virginia CS 655 14

Mastiff: BARK with Manifest Types Program : : = Declaration* Instruction* Declaration : : = TYPE Loc INTEGER Loc will hold integral values. | TYPE Loc REAL Loc will hold real values. Instruction : : = STORE Loc Literal Loc gets the value of Literal. Loc must have been declared with the same type as Literal. … (same as Labrador) Mastiff: An excellent guard dog, yet gentle and affectionate to its family. Walter & Shackles Guide to Dogs 1 Feb 2000 University of Virginia CS 655 15

Mastiff Program [D 0] [D 1] [0] [1] [2] [3] 1 Feb 2000 TYPE R 0 REAL TYPE R 1 INTEGER STORE R 0 3. 14159 STORE R 1 4 MUL R 1 MUL R 0 R 1 University of Virginia CS 655 16

Input Function: I: Program C C = Instructions x PC x Register. File where Instructions = same as before, PC = 0 Register. File[n] = <integer, 0> if TYPE Rn INTEGER is in Declarations Register. File[n] = <real, 0. 0> if TYPE Rn REAL is in Declarations Register. File[n] = <undeclared, 0> for all other integers n Register. File[n] = <error, 0> if (TYPE Rn INTEGER and TYPE Rn REAL are in Declarations) 1 Feb 2000 University of Virginia CS 655 17

STORE Loc Int. Literal Instructions[PC] = STORE Loc Int. Literal, typeof(Register. File[Loc]) = integer < Instructions x PC x Register. File > < Instructions x PC’ x Register. File’ > where PC’ = PC + 1 Register. File’[n] = Register. File[n] if n Loc Register. File’[n] = <integer, value of Int. Literal> if n Loc 1 Feb 2000 University of Virginia CS 655 18

Static Semantics • Static checking = at compile-time – Dynamic checking = at run (simulate)-time • Know a whole program is type-correct without running it • Can make claims about all possible executions • Drawbacks: – May limit expressiveness of types (not everything can be checked statically) – Some type-correct programs may not pass static checking 1 Feb 2000 University of Virginia CS 655 19

Typing Rules Premise; . . . ; Premise Conclusions are type judgments: A E : T Read: A proves E has type T. Use type okay to mean it type-checks, but has no type. Type environment: A Type bindings: [I 1: T 1, . . . , In: Tn] In (Loc) has type Tn 1 Feb 2000 University of Virginia CS 655 20

Mastiff Typing Rules true A Int. Literal : integer [int-literal] Real. Literal : real [real-literal] A contains [Loc: T] Loc : T [location] 1 Feb 2000 University of Virginia CS 655 21

Typing ADD A Loc 1 : integer, A Loc 22 : integer A ADD Loc 1 Loc 2 : okay [add-integers] A Loc 1 : real , A Loc 22 : real A ADD Loc 1 Loc 2 : okay [add-reals] 1 Feb 2000 University of Virginia CS 655 22

Typing MUL A Loc 1 : integer, A Loc 22 : integer A MUL Loc 1 Loc 2 : okay [mul-integers] A Loc 1 : real, A Loc 2 : integer A MUL Loc 1 Loc 2 : okay [mul-weak] 1 Feb 2000 University of Virginia CS 655 23

Typing IF A Loc 1 : integer, A Loc 2 : integer A IF Loc 1 THEN Loc 2 : okay A Loc 1 : real , A Loc 2 : integer A IF Loc 1 THEN Loc 2 : okay 1 Feb 2000 University of Virginia CS 655 [if] [if-weak] 24

Type Checking • Statement is well-typed if and only if it has a provable type judgment: – Construct a proof tree, where the root is the type judgment for this statement, and leaves are the axioms • Declarations provide the axioms: Declarations = TYPE Loci 0 Ti 0; TYPE Loci 1 Ti 1, . . . A = [Loci 0: Ti 0, Loci 1 : Ti 1, . . . ] 1 Feb 2000 University of Virginia CS 655 25

[D 0] [D 1] [0] [1] [2] [3] TYPE R 0 REAL TYPE R 1 INTEGER STORE R 0 3. 14159 STORE R 1 4 MUL R 1 MUL R 0 R 1 Type Checking Example Check instruction 3: MUL R 0 R 1 A = [R 0: real; R 1: integer] from Declarations A contains [R 0 : real] R 0 : real same for R 1: integer A R 0 : real, A R 1 : integer A MUL R 0 R 1 : okay 1 Feb 2000 University of Virginia CS 655 [mul-weak] 26

Mastiff with Expressions Program : : = Declaration* Instruction : : = STORE Loc Expression must match declared type of Loc | GOTO Expression must be integer | IF Expressionp THEN Expressionj must be integer Expression : : = MUL Expression | ADD Expression | Loc | Literal | ( Expression ) 1 Feb 2000 University of Virginia CS 655 27

Type checking Example [D 0] TYPE R 0 REAL [0] STORE R 0 (MUL 3. 14159 (MUL 4 4)) … [real-literal] … [mul-int] A 3. 14: real, A (MUL 4 4) : integer [mul-weak] A MUL 3. 14 (MUL 4 4): okay A R 0 : real, A (MUL …): real A STORE R 0 (MUL …): okay 1 Feb 2000 University of Virginia CS 655 [store-real] 28

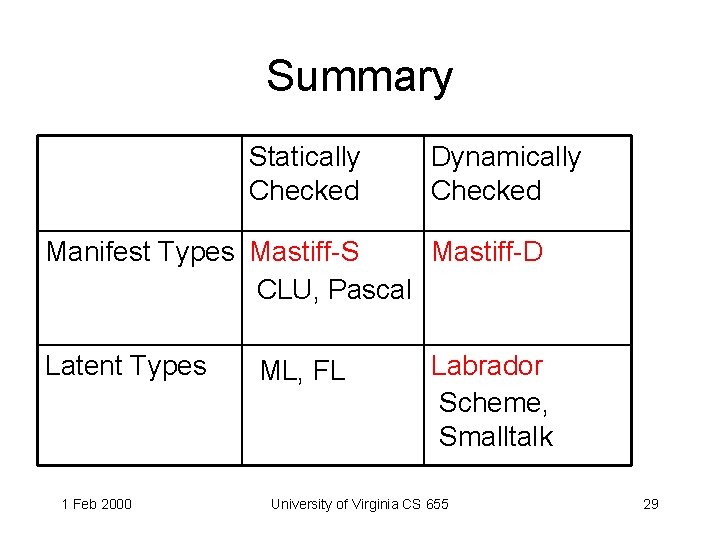
Summary Statically Checked Dynamically Checked Manifest Types Mastiff-S Mastiff-D CLU, Pascal Latent Types 1 Feb 2000 ML, FL Labrador Scheme, Smalltalk University of Virginia CS 655 29

Charge • Continue working on your projects! • Tuesday: Data Abstraction – CLU: language designed to support methodology based on data abstraction – Reasoning (informally) about data abstractions • Next: Object-Oriented Languages • Later: (after Spring Break) – How to do static checking with latent types (type reconstruction, type inference) – How to use types for security • Today at 4: 00, Jordan Hall: Mark S. Boguski, Natl Institutes of Health Interface between computation and biology 1 Feb 2000 University of Virginia CS 655 30