Lecture 6 The Finite Element Method 1 dimensional

Lecture 6; The Finite Element Method 1 -dimensional spring systems Lecture 6; The Finite Element Method 1 1 -dimensional spring systems (modified 2011 -09 -21)

With a 1 -dimensional spring system we here mean springs in series where the individual springs are linear, i. e. expose linear force-elongation relations Note that the identity of a spring is indicated by a ring-symbol, while its stiffness is referred to as k Lecture 6; The Finite Element Method 2 1 -dimensional spring systems (modified 2011 -09 -21)

Why study (linear) spring systems? • You are familiar with springs, since you have met them in a number of courses • By using what you already know (e. g. equilibrium), we may find a matrix formulation which has the same structure as an FE-formulation for a general elastostatic problem of Solid Mechanics Lecture 6; The Finite Element Method 3 1 -dimensional spring systems (modified 2011 -09 -21)

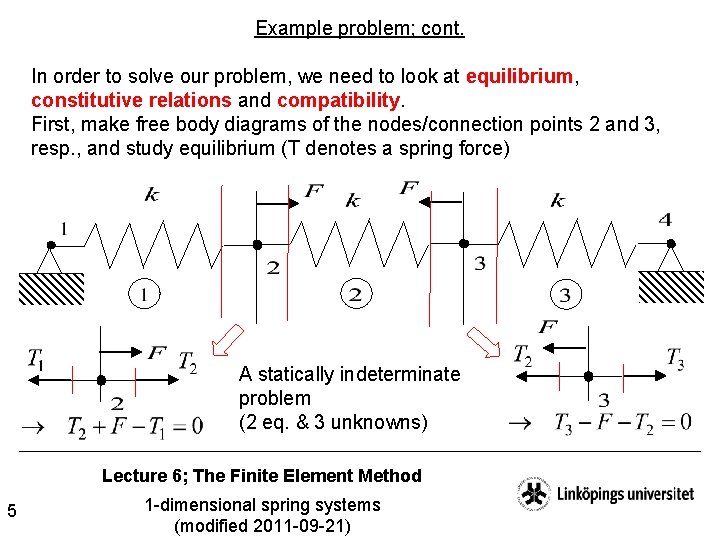
Example problem Let us first, in order to have something to compare with, in the "traditional" way determine the spring forces and spring elongations in the example below. We will later on solve the same problem by a structured FE-treatment. Lecture 6; The Finite Element Method 4 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. In order to solve our problem, we need to look at equilibrium, constitutive relations and compatibility. First, make free body diagrams of the nodes/connection points 2 and 3, resp. , and study equilibrium (T denotes a spring force) A statically indeterminate problem (2 eq. & 3 unknowns) Lecture 6; The Finite Element Method 5 1 -dimensional spring systems (modified 2011 -09 -21)

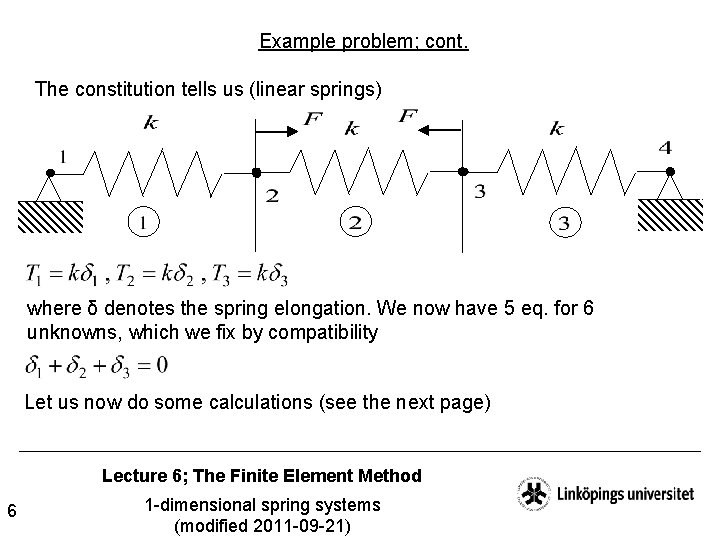
Example problem; cont. The constitution tells us (linear springs) where δ denotes the spring elongation. We now have 5 eq. for 6 unknowns, which we fix by compatibility Let us now do some calculations (see the next page) Lecture 6; The Finite Element Method 6 1 -dimensional spring systems (modified 2011 -09 -21)

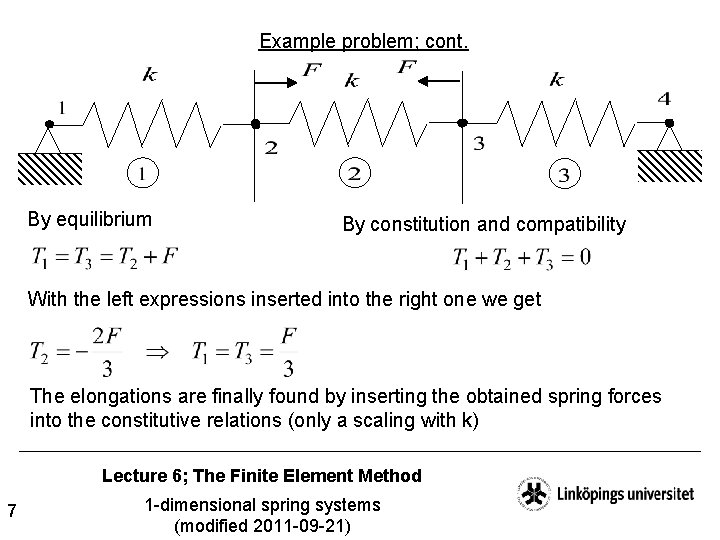
Example problem; cont. By equilibrium By constitution and compatibility With the left expressions inserted into the right one we get The elongations are finally found by inserting the obtained spring forces into the constitutive relations (only a scaling with k) Lecture 6; The Finite Element Method 7 1 -dimensional spring systems (modified 2011 -09 -21)

Structured analysis of spring systems Let us now focus on a general structured FE approach for spring systems, which contains the following steps I. Find, for each spring, a relation between the spring loading and the spring displacements II. Find, for the spring structure, a relation between the structural loading and the structural displacements III. Solve the structural problem for the given loading and restraints, and calculate entities such as spring forces and spring elongations Let us now see how this is done! Lecture 6; The Finite Element Method 8 1 -dimensional spring systems (modified 2011 -09 -21)

Step I Find, for each spring, a relation between spring loading and the spring displacements Lecture 6; The Finite Element Method 9 1 -dimensional spring systems (modified 2011 -09 -21)

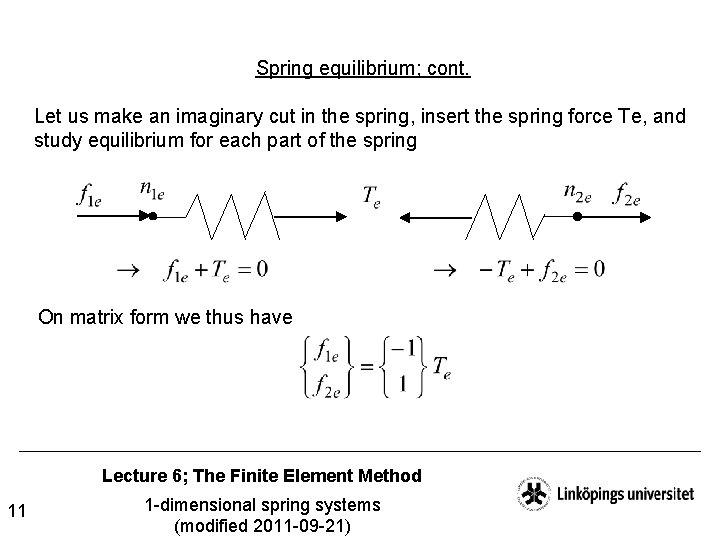
Spring equilibrium Let us now study equilibrium for an arbitrary spring in a spring system as illustrated below, where the index e refers to the element number, where the spring nodes/end points are labeled n 1 e and n 2 e, resp. , and where the spring loading is described by the forces f 1 e and f 2 e, resp. Note that the forces are defined positive in the positive x-direction! Lecture 6; The Finite Element Method 10 1 -dimensional spring systems (modified 2011 -09 -21)

Spring equilibrium; cont. Let us make an imaginary cut in the spring, insert the spring force Te, and study equilibrium for each part of the spring On matrix form we thus have Lecture 6; The Finite Element Method 11 1 -dimensional spring systems (modified 2011 -09 -21)

Spring equilibrium; cont. Let us now proceed and look at the spring deformation, where the elongation (as before) is labeled δe, while the displacement of its end nodes are called d 1 e and d 2 e; resp. Obviously or, on matrix form Lecture 6; The Finite Element Method 12 1 -dimensional spring systems (modified 2011 -09 -21)

Spring equilibrium; cont. Since the springs are linear, we have Lecture 6; The Finite Element Method 13 1 -dimensional spring systems (modified 2011 -09 -21)

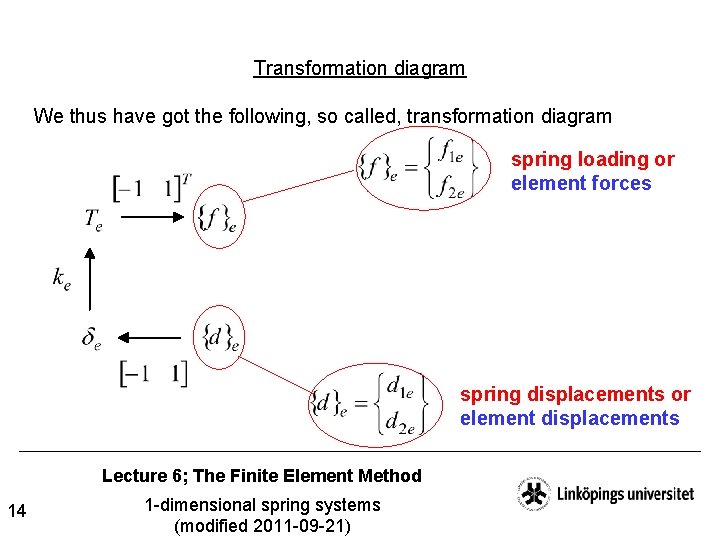
Transformation diagram We thus have got the following, so called, transformation diagram spring loading or element forces spring displacements or element displacements Lecture 6; The Finite Element Method 14 1 -dimensional spring systems (modified 2011 -09 -21)

Transformation diagram; cont. A counter-clockwise trip in the transf. diag. will give us the so called spring stiffness [k]e, which relates the element displacements to the element forces Lecture 6; The Finite Element Method 15 1 -dimensional spring systems (modified 2011 -09 -21)

Transformation diagram; cont. The complete transf. diag. for the spring thus takes the form Lecture 6; The Finite Element Method 16 1 -dimensional spring systems (modified 2011 -09 -21)

Step II Find, for the spring structure, the relation between the structual loading and the structural displacements Lecture 6; The Finite Element Method 17 1 -dimensional spring systems (modified 2011 -09 -21)

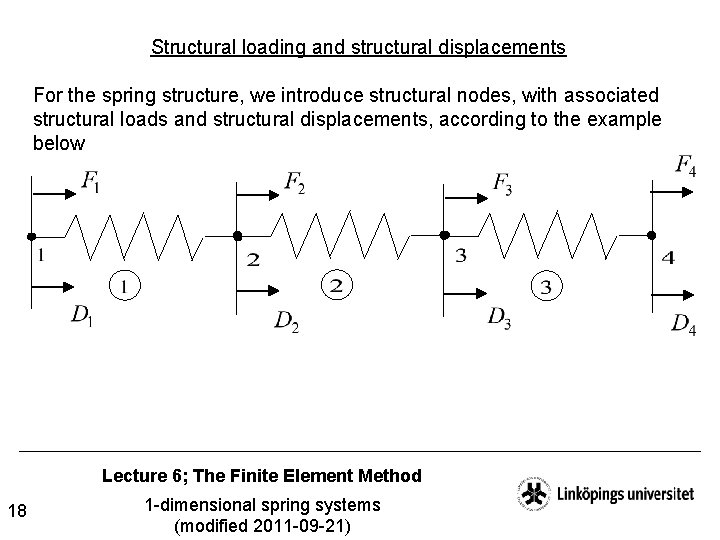
Structural loading and structural displacements For the spring structure, we introduce structural nodes, with associated structural loads and structural displacements, according to the example below Lecture 6; The Finite Element Method 18 1 -dimensional spring systems (modified 2011 -09 -21)

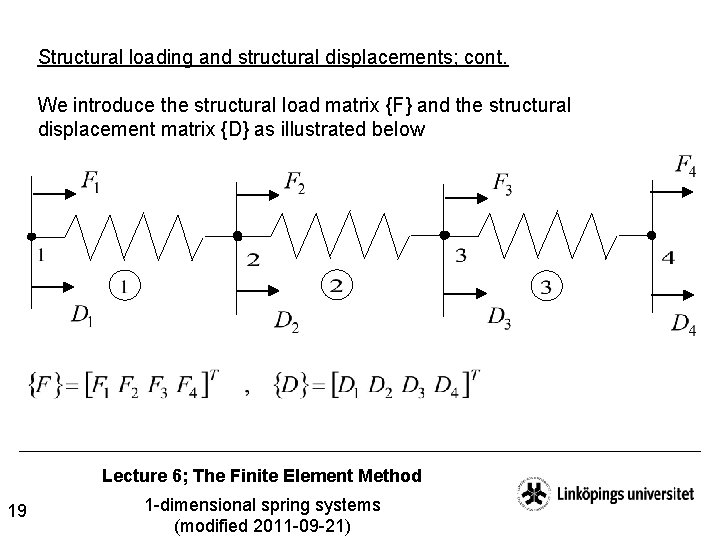
Structural loading and structural displacements; cont. We introduce the structural load matrix {F} and the structural displacement matrix {D} as illustrated below Lecture 6; The Finite Element Method 19 1 -dimensional spring systems (modified 2011 -09 -21)

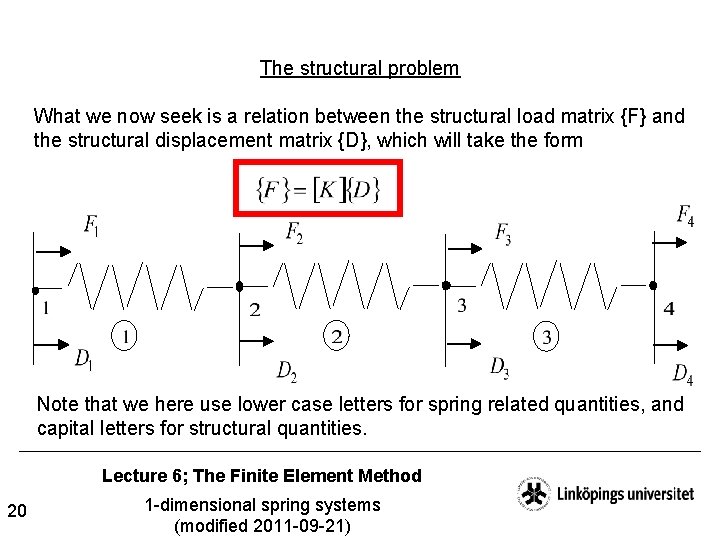
The structural problem What we now seek is a relation between the structural load matrix {F} and the structural displacement matrix {D}, which will take the form Note that we here use lower case letters for spring related quantities, and capital letters for structural quantities. Lecture 6; The Finite Element Method 20 1 -dimensional spring systems (modified 2011 -09 -21)

The structural problem; cont. In the transformation diagram we thus have to find Lecture 6; The Finite Element Method 21 1 -dimensional spring systems (modified 2011 -09 -21)

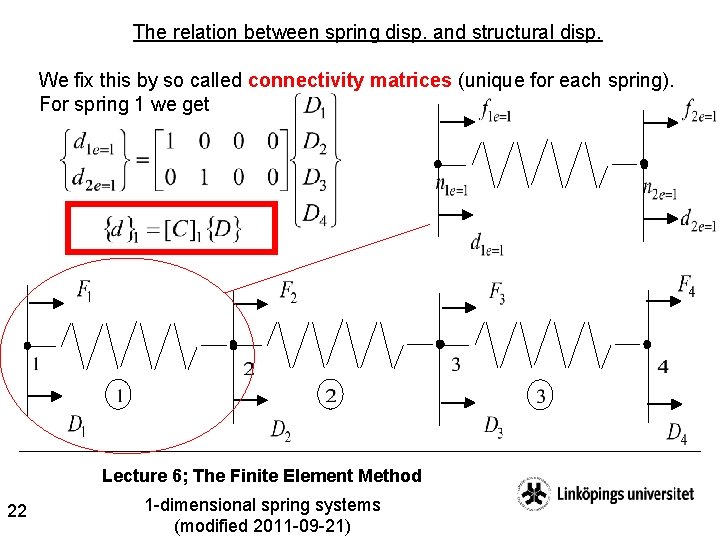
The relation between spring disp. and structural disp. We fix this by so called connectivity matrices (unique for each spring). For spring 1 we get Lecture 6; The Finite Element Method 22 1 -dimensional spring systems (modified 2011 -09 -21)

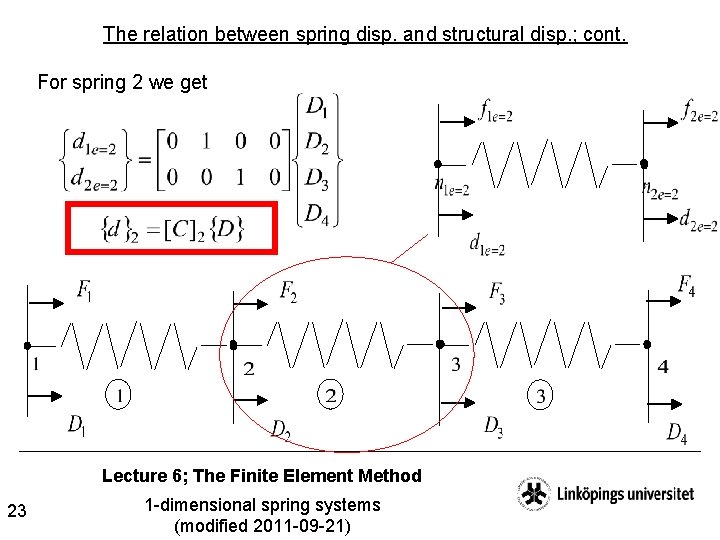
The relation between spring disp. and structural disp. ; cont. For spring 2 we get Lecture 6; The Finite Element Method 23 1 -dimensional spring systems (modified 2011 -09 -21)

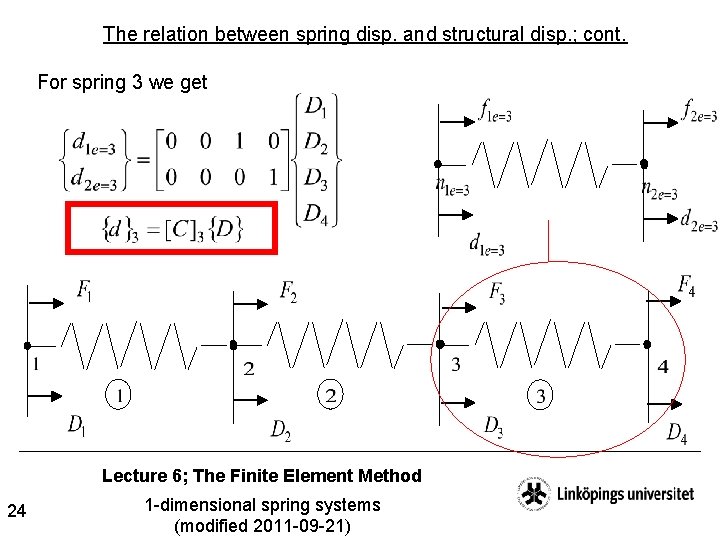
The relation between spring disp. and structural disp. ; cont. For spring 3 we get Lecture 6; The Finite Element Method 24 1 -dimensional spring systems (modified 2011 -09 -21)

The relation between spring disp. and structural disp. ; cont. Thus, Lecture 6; The Finite Element Method 25 1 -dimensional spring systems (modified 2011 -09 -21)

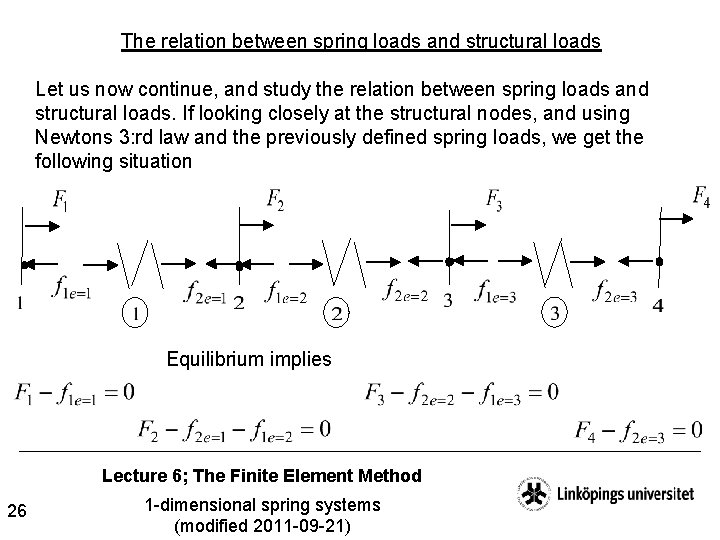
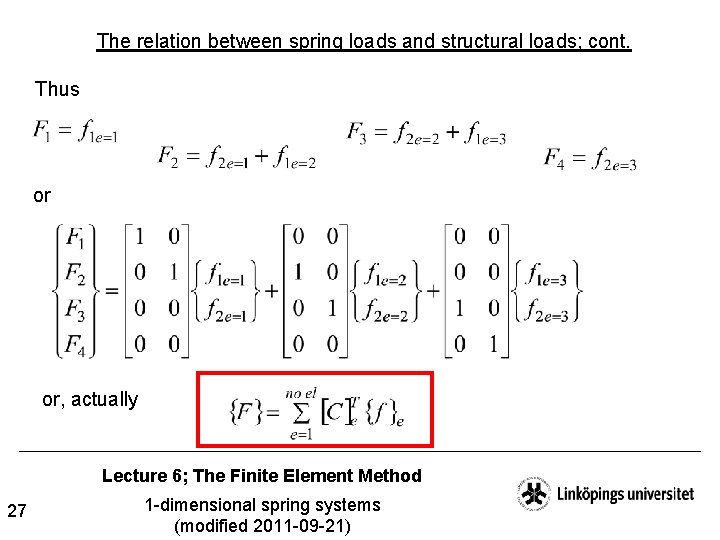
The relation between spring loads and structural loads Let us now continue, and study the relation between spring loads and structural loads. If looking closely at the structural nodes, and using Newtons 3: rd law and the previously defined spring loads, we get the following situation Equilibrium implies Lecture 6; The Finite Element Method 26 1 -dimensional spring systems (modified 2011 -09 -21)

The relation between spring loads and structural loads; cont. Thus or or, actually Lecture 6; The Finite Element Method 27 1 -dimensional spring systems (modified 2011 -09 -21)

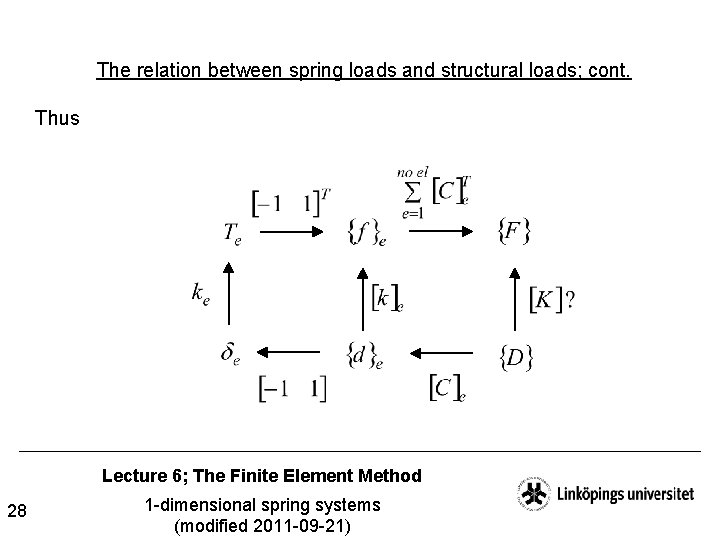
The relation between spring loads and structural loads; cont. Thus Lecture 6; The Finite Element Method 28 1 -dimensional spring systems (modified 2011 -09 -21)

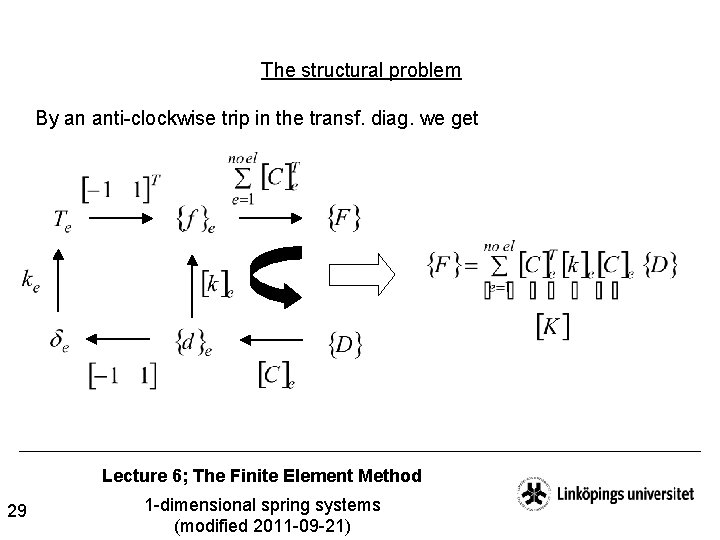
The structural problem By an anti-clockwise trip in the transf. diag. we get Lecture 6; The Finite Element Method 29 1 -dimensional spring systems (modified 2011 -09 -21)

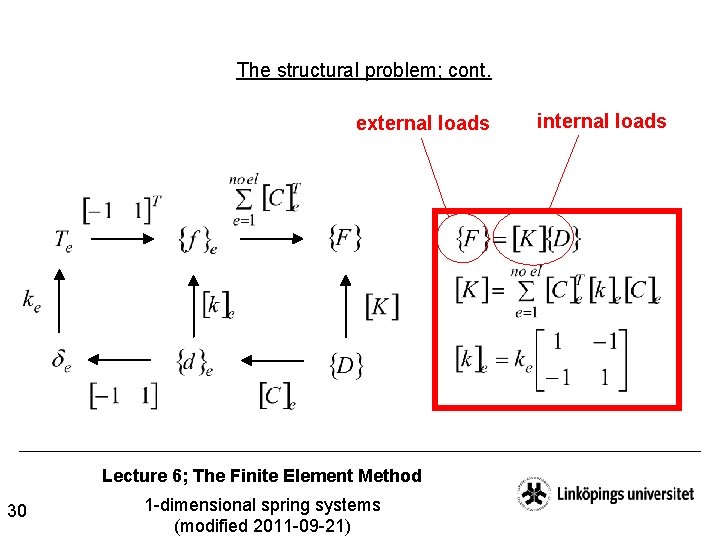
The structural problem; cont. external loads Lecture 6; The Finite Element Method 30 1 -dimensional spring systems (modified 2011 -09 -21) internal loads

Step III Solve the structural problem for given loading and restraints, and calculate entities such as spring forces and spring elongations Let us see what this looks like in our example! Lecture 6; The Finite Element Method 31 1 -dimensional spring systems (modified 2011 -09 -21)

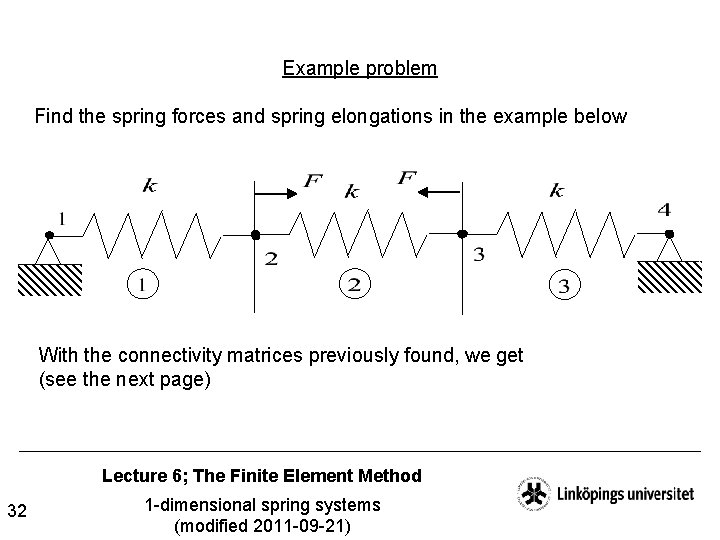
Example problem Find the spring forces and spring elongations in the example below With the connectivity matrices previously found, we get (see the next page) Lecture 6; The Finite Element Method 32 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. Lecture 6; The Finite Element Method 33 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. We thus have to solve Lecture 6; The Finite Element Method 34 1 -dimensional spring systems (modified 2011 -09 -21) =0 =? =F =? =-F =0 =?

Example problem; cont. The unknown displacements D 2 and D 3 are now found by solving the equation system one gets when eliminating all rows and columns associated with locked displacements implying Lecture 6; The Finite Element Method 35 1 -dimensional spring systems (modified 2011 -09 -21) =0 =? =F =? =-F =0 =?

Example problem; cont. The spring elongations are then found by (c. f. the transformation diagram) which for instance gives Finally, the spring forces are found by (c. f. the transformation diagram) Implying e. g. that As before : ) Lecture 6; The Finite Element Method 36 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. The way used for finding the structural problem described above (assembling the spring stiffnesses by using connectivity matrices) constitutes the general structured way to describe FEM. In a hand calculation situation, it is often easier to use the procedure described below (not using connectivity matrices). Also when considering implementation in a computer code it is generally too expensive to directly work with connectivity matrices (both with respect to computational time and memory allocation). Instead one saves the positions of the non-zero elements in the connectivity matrices. Lecture 6; The Finite Element Method 37 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. The “direct identification” method The contribution to [K] from element 1, which we here call [K]1, is = D 1 = D 2 Lecture 6; The Finite Element Method 38 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. The “direct identification” method; cont. The contribution to [K] from element 2, which we here call [K]2, is = D 2 = D 3 Lecture 6; The Finite Element Method 39 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. The “direct identification” method; cont. The contribution to [K] from element 3, which we here call [K]3, is = D 3 = D 4 Lecture 6; The Finite Element Method 40 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. The “direct identification” method; cont. The resulting structural stiffness is found by adding all contributions (giving the same result as before) Lecture 6; The Finite Element Method 41 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. The “direct identification” method; cont. After having solved the structural problem, we proceed in the following way when calculating the spring forces (note that we in the “direct identification” procedure have not set up any connectivity matrices). Lecture 6; The Finite Element Method 42 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. The “direct identification” method; cont. As an example, we get for element 1 T 1 =k = D 1 = D 2 Lecture 6; The Finite Element Method 43 1 -dimensional spring systems (modified 2011 -09 -21) As before : )

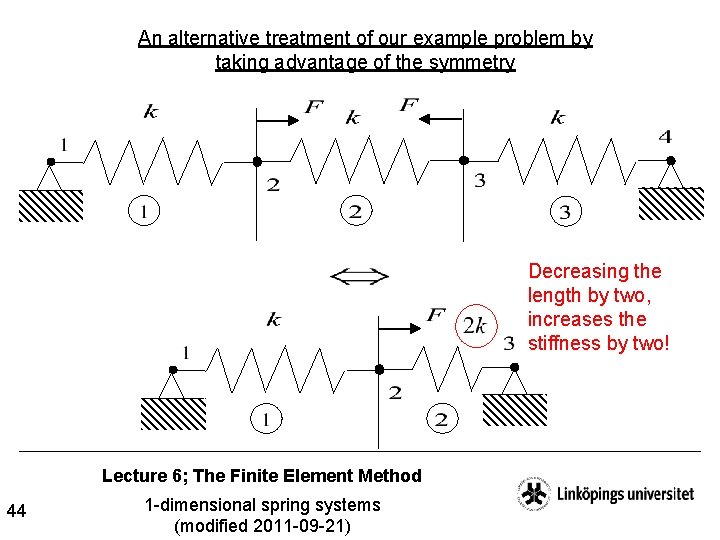
An alternative treatment of our example problem by taking advantage of the symmetry Decreasing the length by two, increases the stiffness by two! Lecture 6; The Finite Element Method 44 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. The contribution to [K] from element 1, which we here call [K]1, is = D 1 = D 2 Lecture 6; The Finite Element Method 45 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. The contribution to [K] from element 2, which we here call [K]2, is = D 2 = D 3 Lecture 6; The Finite Element Method 46 1 -dimensional spring systems (modified 2011 -09 -21)

Example problem; cont. We thus have to solve =0 =? =F =0 =? and gets =F As before : ) Lecture 6; The Finite Element Method 47 1 -dimensional spring systems (modified 2011 -09 -21)

Some final comments The spring stiffness matrix [k]e and the structural stiffness matrix [K] are symmetric and singular (can not be inverted). However, if we have prevented rigid body motions, we may solve the structural problem (the reduced stiffness matrix obtained by removing rows and columns associated with locked displacements is not singular). One may finally also note that the sum of all components in a row or column of [k]e or [K] is always zero. Lecture 6; The Finite Element Method 48 1 -dimensional spring systems (modified 2011 -09 -21)