Lecture 6 Stacks 1 The Abstract Data Type

Lecture 6: Stacks 1

The Abstract Data Type • Specifications of an abstract data type for a particular problem – Can emerge during the design of the problem’s solution – Examples • read. And. Correct algorithm • display. Backward algorithm 2

Developing an ADT During the Design of a Solution • ADT stack operations – Create an empty stack – Destroy a stack – Determine whether a stack is empty – Add a new item to the stack – Remove the item that was added most recently – Retrieve the item that was added most recently 3

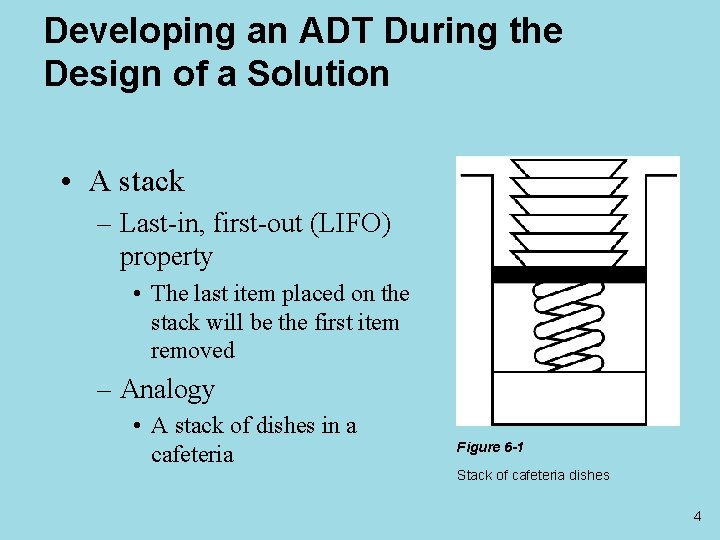
Developing an ADT During the Design of a Solution • A stack – Last-in, first-out (LIFO) property • The last item placed on the stack will be the first item removed – Analogy • A stack of dishes in a cafeteria Figure 6 -1 Stack of cafeteria dishes 4

Refining the Definition of the ADT Stack • Operation Contract for the ADT Stack is. Empty(): boolean {query} push(in new. Item: Stack. Item. Type) throw Stack. Exception pop(out stack. Top: Stack. Item. Type) throw Stack. Exception get. Top(out stack. Top: Stack. Item. Type) {query} throw Stack. Exception 5

Implementations of the ADT Stack • The ADT stack can be implemented using – An array – A linked list – The ADT list • All three implementations use a Stack. Exception class to handle possible exceptions 6

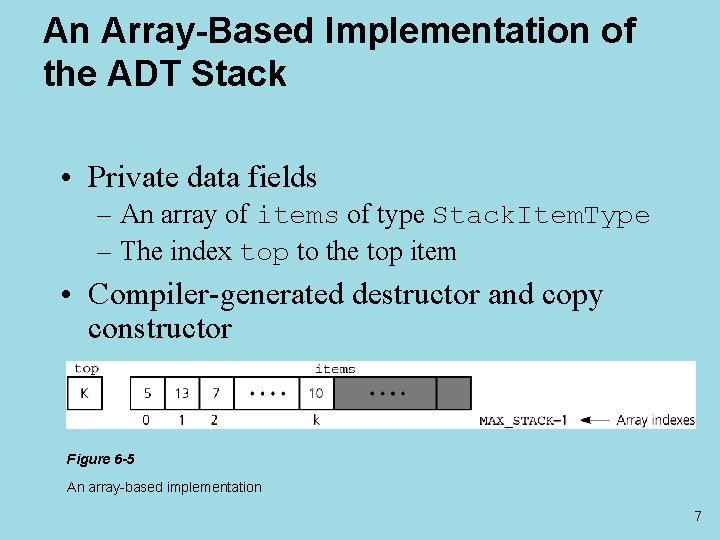
An Array-Based Implementation of the ADT Stack • Private data fields – An array of items of type Stack. Item. Type – The index top to the top item • Compiler-generated destructor and copy constructor Figure 6 -5 An array-based implementation 7

• const int MAX_STACK = 20; • typedef int Stack. Item. Type; • • • • class Stack { public: Stack(); // default constructor bool is. Empty() const; void push(Stack. Item. Type new. Item) ; void pop(Stack. Item. Type& stack. Top); void get. Top(Stack. Item. Type& stack. Top) const; private: Stack. Item. Type items[MAX_STACK]; // array of stack items int top; // index to top of stack }; // end class

• Stack: : Stack(): top(-1) • { • }; // end default constructor • bool Stack: : is. Empty() const • { • return top < 0; • }; // end is. Empty

• void Stack: : push(Stack. Item. Type new. Item) throw(Stack. Exception) • {// if stack has no more room for another item • if (top >= MAX_STACK-1) • throw Stack. Exception("Stack. Exception: stack full on push"); • else • { ++top; • items[top] = new. Item; • } // end if • }; // end push • void Stack: : pop() throw(Stack. Exception) • { • if (is. Empty()) • throw Stack. Exception("Stack. Exception: stack empty on pop"); • else • --top; // stack is not empty; pop top • }; // end pop 10

• • • void Stack: : pop(Stack. Item. Type& stack. Top) throw(Stack. Exception) { if (is. Empty()) throw Stack. Exception("Stack. Exception: stack empty on pop"); else { // stack is not empty; retrieve top stack. Top = items[top]; --top; // pop top } // end if }; // end pop • • void Stack: : get. Top(Stack. Item. Type& stack. Top) const throw(Stack. Exception) { if (is. Empty()) throw Stack. Exception("Stack. Exception: stack empty on get. Top"); else // stack is not empty; retrieve top stack. Top = items[top]; }; // end get. Top 11

• • • • int main() { Stack. Item. Type an. Item; Stack a. Stack; for (int i = 0; i< 10; i++) {an. Item = i*10; a. Stack. push(an. Item); // push it onto stack } while (!a. Stack. is. Empty()) { a. Stack. get. Top(an. Item); cout <<an. Item<<endl; a. Stack. pop(); } return 0; }//ex 6 -1. cpp 12

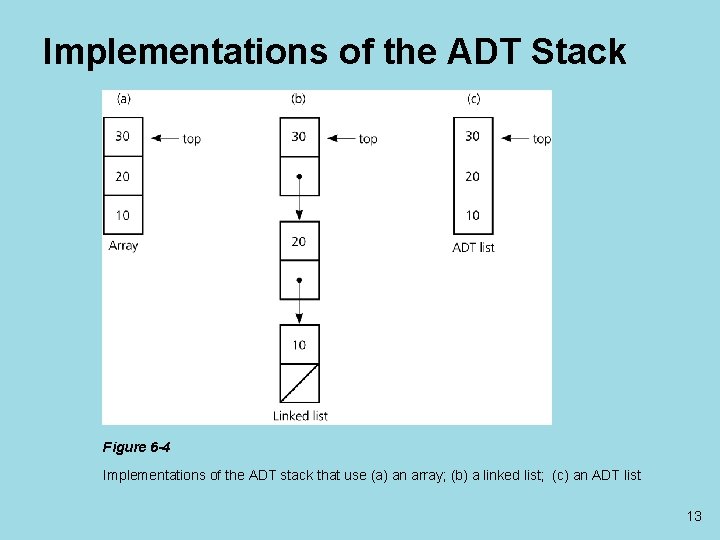
Implementations of the ADT Stack Figure 6 -4 Implementations of the ADT stack that use (a) an array; (b) a linked list; (c) an ADT list 13

A Pointer-Based Implementation of the ADT Stack • A pointer-based implementation – Enables the stack to grow and shrink dynamically • top. Ptr is a pointer to the head of a linked list of items • A copy constructor and destructor must be supplied Figure 6 -6 A pointer-based implementation 14

Pointer-based Stack • • • • class Stack {public: //… Stack(const Stack& a. Stack); //… ~Stack(); //Destructor; private: struct Stack. Node // a node on the stack { Stack. Item. Type item; // a data item on the stack Stack. Node *next; // pointer to next node }; // end struct Stack. Node *top. Ptr; // pointer to first node in the stack }; // end class 15

• • • • • Stack: : Stack() : top. Ptr(NULL) {} // end default constructor Stack: : Stack(const Stack& a. Stack) { if (a. Stack. top. Ptr == NULL) top. Ptr = NULL; // original list is empty else { // copy first node top. Ptr = new Stack. Node; top. Ptr->item = a. Stack. top. Ptr->item; // copy rest of list Stack. Node *new. Ptr = top. Ptr; // new list pointer for (Stack. Node *orig. Ptr = a. Stack. top. Ptr->next; orig. Ptr != NULL; orig. Ptr = orig. Ptr->next) { new. Ptr->next = new Stack. Node; new. Ptr = new. Ptr->next; new. Ptr->item = orig. Ptr->item; } // end for new. Ptr->next = NULL; } // end if } // end copy constructor 16

• Stack: : ~Stack() • {while (!is. Empty()) pop(); } // Assertion: top. Ptr == NULL • bool Stack: : is. Empty() const • { return top. Ptr == NULL; } // end is. Empty • void Stack: : push(Stack. Item. Type new. Item) • { // create a new node • Stack. Node *new. Ptr = new Stack. Node; • // set data portion of new node • new. Ptr->item = new. Item; • // insert the new node • new. Ptr->next = top. Ptr; • top. Ptr = new. Ptr; • } // end push 17

• void Stack: : pop() throw(Stack. Exception) • { • if (is. Empty()) • throw Stack. Exception("Stack. Exception: stack empty on pop"); • else • { // stack is not empty; delete top • Stack. Node *temp = top. Ptr; • top. Ptr = top. Ptr->next; • // return deleted node to system • temp->next = NULL; // safeguard • delete temp; • } // end if • } // end pop 18

• • • • • void Stack: : pop(Stack. Item. Type& stack. Top) throw(Stack. Exception) {if (is. Empty()) throw Stack. Exception("Stack. Exception: stack empty on pop"); else { // stack is not empty; retrieve and delete top stack. Top = top. Ptr->item; Stack. Node *temp = top. Ptr; top. Ptr = top. Ptr->next; temp->next = NULL; // safeguard delete temp; // return deleted node to system } // end if } // end pop void Stack: : get. Top(Stack. Item. Type& stack. Top) const throw(Stack. Exception) { if (is. Empty()) throw Stack. Exception("Stack. Exception: stack empty on get. Top"); else // stack is not empty; retrieve top stack. Top = top. Ptr->item; } // end get. Top //ex 6 -2. cpp 19

An Implementation That Uses the ADT List • The ADT list can represent the items in a stack • Let the item in position 1 of the list be the top – push(new. Item) • insert(1, new. Item) – pop() • remove(1) – get. Top(stack. Top) • retrieve(1, stack. Top) 20

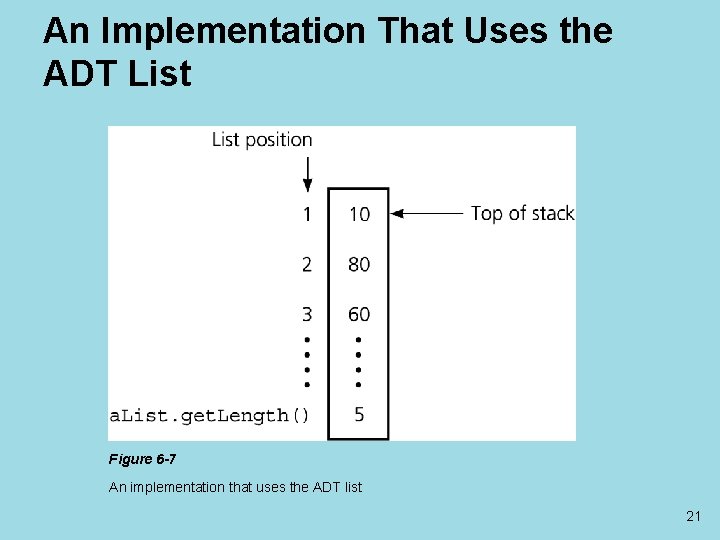
An Implementation That Uses the ADT List Figure 6 -7 An implementation that uses the ADT list 21

Comparing Implementations • Fixed size versus dynamic size – A statically allocated array-based implementation • Fixed-size stack that can get full • Prevents the push operation from adding an item to the stack, if the array is full – A dynamically allocated array-based implementation or a pointer-based implementation • No size restriction on the stack 22

Comparing Implementations • A pointer-based implementation vs. one that uses a pointer-based implementation of the ADT list – Pointer-based implementation is more efficient – ADT list approach reuses an already implemented class • Much simpler to write • Saves programming time 23

List Based Stack • • • Stack {public: //… private: List a. List; // list of stack items }; // others are the same as the Pointer-based 24

• Stack: : Stack() • { } // end default constructor • Stack: : Stack(const Stack& a. Stack): a. List(a. Stack. a. List) • { } // end copy constructor • Stack: : ~Stack() • { } // end destructor • bool Stack: : is. Empty() const • { • return a. List. is. Empty(); • } // end is. Empty 25

• void Stack: : push(Stack. Item. Type new. Item) throw(Stack. Exception) • { try { • a. List. insert(1, new. Item); • } // end try • catch (List. Exception e) • { throw Stack. Exception("Stack. Exception: cannot push item"); • } // end catch • } // end push • void Stack: : pop() throw(Stack. Exception) • { try { • a. List. remove(1); • } // end try • catch (List. Index. Out. Of. Range. Exception e) • { throw Stack. Exception("Stack. Exception: stack empty on pop"); • } // end catch • } // end pop 26

• • • void Stack: : pop(Stack. Item. Type& stack. Top) throw(Stack. Exception) { try { a. List. retrieve(1, stack. Top); a. List. remove(1); } // end try catch (List. Index. Out. Of. Range. Exception e) { throw Stack. Exception("Stack. Exception: stack empty on pop"); } // end catch } // end pop • • • void Stack: : get. Top(Stack. Item. Type& stack. Top) const throw(Stack. Exception) { try { a. List. retrieve(1, stack. Top); } // end try catch (List. Index. Out. Of. Range. Exception e) { throw Stack. Exception("Stack. Exception: stack empty on get. Top"); } // end catch } // end get. Top //ex 6 -3. cpp 27

The STL Class stack • Provides a size function • Has two data type parameters – T, the data type for the stack items – Container, the container class that the STL uses in its implementation of the stack • Uses the keyword explicit in the constructor’s declaration to prevent use of the assignment operator to invoke the constructor 28

• • • • • #include <iostream> #include <stack> using namespace std; int main() { stack<int> a. Stack; int item; // Right now, the stack is empty if (a. Stack. empty()) cout << "The stack is empty. " << endl; for (int j = 0; j < 5; j++) a. Stack. push(j); // places items on top of stack while (!a. Stack. empty()) { cout << a. Stack. top() << endl; a. Stack. pop(); } // end while return 0; } // end main //ex 6 -4. cpp 29

Using the ADT Stack in a Solution • A program can use a stack independently of the stack’s implementation – display. Backward algorithm can be refined using stack operations • Use axioms to define an ADT stack formally – Example: Specify that the last item inserted is the first item to be removed (a. Stack. push(new. Item)). pop()= a. Stack 30

Checking for Balanced Braces • A stack can be used to verify whether a program contains balanced braces – An example of balanced braces abc{defg{ijk}{l{mn}}op}qr – An example of unbalanced braces abc{def}}{ghij{kl}m 31

Checking for Balanced Braces • Requirements for balanced braces – Each time you encounter a “}”, it matches an already encountered “{” – When you reach the end of the string, you have matched each “{” 32

Checking for Balanced Braces Figure 6 -3 Traces of the algorithm that checks for balanced braces 33

34 bool balanced (string str) • { int index=0; • Stack S; • while (str [index]!= '') { • if (str[index] == ‘{' ) • S. push(‘{'); • else if(str[index] == ‘}' ) { • if(!S. is. Empty( )) S. pop( ); • else return 0; • } • ++index; // next character • } • return (S. is. Empty( ));

Recognizing Languages 35 We define a language L as follows: L = {w$w’| w is a character string that does not contain a $ sign. w’ is the reverse of w. } PALINDROMES EXAMPLES: A$A AB$BA ABA$ABA // in language Counter Examples: A$B$B$A A$BA //not in language Basic Idea: Keep pushing characters onto a stack until you see a $. Then keep popping and reading, and compare those characters. Return FALSE if a popped character is different from a read character. Return TRUE if the stack becomes empty and the end of the string is found at the same time.

36 bool palindrome (string str) • { int index=0; Stack S; • while (str[index] != '$') { • if (str[index] == '') return false; • S. push(str[index]); • ++index; } • ++index; char ch; • while (str[index] != '') { • if (S. is. Empty( )) return false; • S. get. Top(ch); • if (ch != str[index] ) return false; • S. pop( ); • ++index; } • if (S. is. Empty( )) return true; // should be! • else return false; • } //ex 6 -5. cpp

37 Evaluating Postfix Expressions: Given is a postfix expression, compute its value. 2 * (3 + 4) (infix) 2 3 4 + * (corresponding postfix) 2 * (3 + 4) -> 14 2 3 4 + * -> 14

38 Basic Idea: We use a stack again, but this time we put the NUMBERS onto it. Every time we see a number, we push it. Every time we see an operator, we pop off two numbers, apply the operator, and push the result back onto the stack. 2 2 3 4 + 3. . . 4 + *. . . Push 2 on the stack. . . Push 3 on the stack. . . Push 4 on the stack. . . Pop off 4; Pop off 3; add 3 and 4; (ORDER!) Push 7 on stack. *. . . Pop off 7; Pop off 2; Multiply 2 and 7; Push 14 back on the stack.

39 Now the same example using the abstract data type. S. Push(2) S. Push(3) S. Push(4) y = S. Get. Stack. Top() S. Pop() x = S. Get. Stack. Top() S. Pop() z=x+y S. Push(z) y = S. Get. Stack. Top() S. Pop() x = S. Get. Stack. Top() S. Pop() z=x*y S. Push(z)

40 For the program we make a number of simplifying assumptions: · No error checking; No unary operators; Only +, -, *, / as operators; and Only digit 1 -9 as operands · int evaluate (string str) • {Stack S; int x, y, z; • for ( int index =0; index< str. length(); ++index) { // look at each char – if (( str[index]=='+' )||(str[index] == '-')||(str[index] == '*')||(str[index] == '/')) { S. get. Top(y); S. pop( ); • S. get. Top(x); S. pop( ); • switch (str[index]){case '+': z = x + y; break; case '-': z = x-y; break; • case '*': z = x*y; break; case '/': z = x/y; break; • } ; S. push(z); • } else S. push(str[index]-'0'); • } • S. get. Top(z); return z; • }

41 Converting Infix to Postfix (Complicated) This uses a stack again, but this time it stores the operators and open parentheses, as opposed to the operands. The result is stored in an array “PE”, the postfix expression. Algorithm 1. If an operand appears in the input stream, then append it to the PE array. 2. If a “(“ appears in the input stream, then push it onto the stack. 3. If a “)” appears in the input stream, then pop off elements from the stack and append them to the PE array until an open parenthesis is found on the stack. Pop off and discard the (

42 4. If an operator appears in the input stream, then: IF the stack is NOT EMPTY then pop off operators of greater or equal precedence from the stack and append them to PE, until: a) either: the stack is empty b) or: you find an “(“ on the stack c) or: you find an operator of lower precedence Then push the new operator on the stack. 5. When you reach the end of the input, then pop off all operators from the stack and append them to the end of PE.

43 Now we will show an example of how to actually do this. We convert: A - (B + C * D) / E We will show the stack top on the RIGHT. CH= A CH= ( CH= B CH= + CH= C CH= * S= S= S= -(+ S= -(+* PE= AB PE= ABC 1. 4. d) 2. 1. 4. b) 1. 4. c) CH= D CH= ) S= -(+* S= -(+ S= -( S= S= -/ S= S= PE= ABCD*+ PE= ABCD*+E/- 1. 3. 3. 3. 4. d) 1. 5. 5. CH= / CH= E

44 Why does this work? This algorithm is based on the following observations: 1) Operands stay in the same order. A+B becomes AB+ and NOT BA+ 2) Operators move only to the right, never to the left, relative to the operands. A+B ---> AB+ + moved to the right of B. 3) Postfix expressions don’t need parenthesis.

• string infix. To. Postfix (string str) • {Stack S; string result; int y; • for ( int index =0; index< str. length(); ++index) { • // look at each char • switch (str[index]) { • case '(': S. push (str[index]); break; • case ')': • if (!S. is. Empty()){ S. pop(y); • while (char (y) !='(') {result+=char(y); S. pop(y); }; • } • break;

• • • case '+': case '-': case '*': case '/': if (!S. is. Empty()){S. get. Top(y); while ((!S. is. Empty())&& (char(y)!='(') &&(pre(str[index])<= pre(y))) { result+=char(y); S. pop(); S. get. Top(y); } } S. push (str[index]); break; default: if (str[index]<='Z'&&str[index]>='A')||(str[index]<='z'&&str[index]> ='a')) result+=str[index]; } }

• while (!S. is. Empty()) {S. pop(y); • if ((char(y) == '+')||(char(y) == '-')||(char(y) == '*')||(char(y) == '/'))result+=char(y); • else return "Error!"; • } • return result; • }

48 Search This section uses a structure called a graph that will be covered in more detail much later in the class. Given is the following problem: There is a map of cities, and there is a flight plan that describes all connections between cities. Then you are given two specific cities, A and B and asked whether you can fly from A to B. Note: In a real flight plan you can’t be sure that there is a flight from B to A. We will use examples that make this assumption. In fact, there will be “dead-end cities” with no flights leaving. (Flights in, No flights out) Of course this problem uses a stack, but we start with the representation of the map.

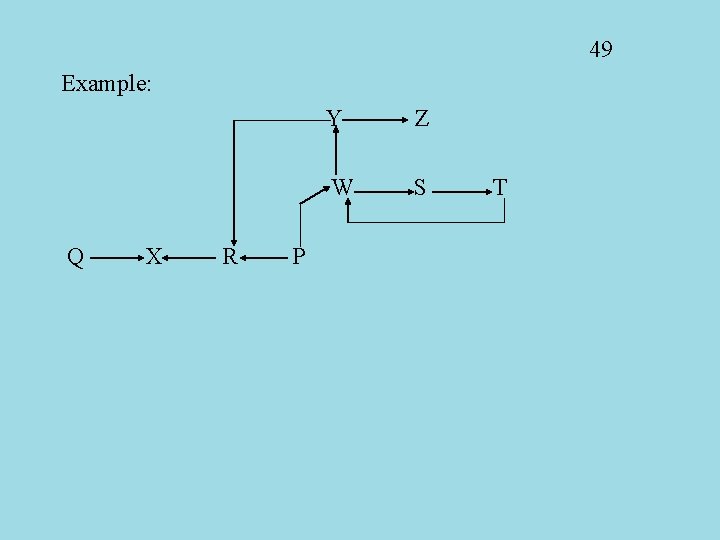
49 Example: Q X R P Y Z W S T

50 How do we represent this “graph” in the computer? There are two possibilities, but for now we will learn only one: The Adjacency List. An adjacency list is really an ARRAY OF LINKED LISTS. For every city there is one element in the array. This element is a pointer to a linked list. Every element of the linked list contains the name of ONE NEIGHBORING CITY.

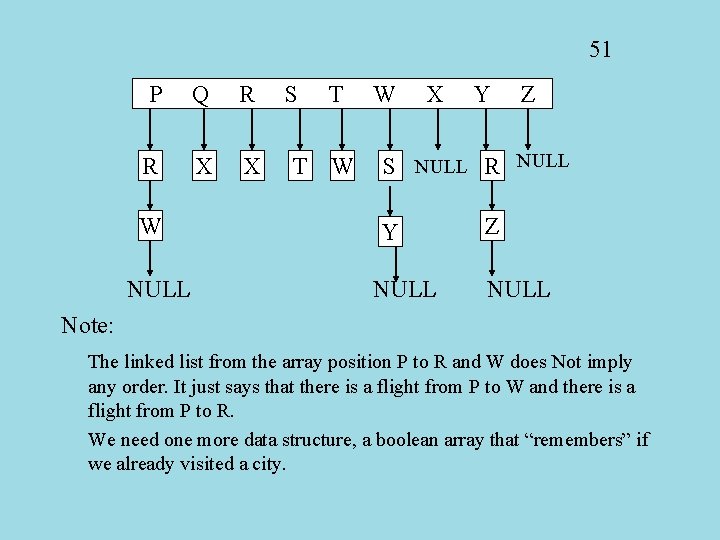
51 P Q R R X X W NULL S T T W W X Y Z S NULL R NULL Y NULL Z NULL Note: The linked list from the array position P to R and W does Not imply any order. It just says that there is a flight from P to W and there is a flight from P to R. We need one more data structure, a boolean array that “remembers” if we already visited a city.

52 Back to the problem: We assume that there are three files: Cityfile. . . A file of cities, in alphabetical order, that are known to all. If there is no flight from or to a city, it is just not mentioned here. Flightfile. . . This is the actual flight plan. Each line contains a pair of cities, and such a line means that there is a flight from the first city to the second city. Requestfile. . . This looks exactly like the Flightfile, but it stands for a request.

53 For the simplest version we want only answer: “you can get there from here, ” or “you cannot get there from here. ” We use a backtrack search to find the path. If necessary we search “exhaustively, ” which means we try every possible path. Let’s call the origin city O, and the destination city D. Either we find a path, or we conclude that no path exists. Basic approach: Look at a neighbor of O. If the neighbor is D, then we are done. If this neighbor is not D, say it is C 1, then we look at a neighbor of C 1. If the neighbor of C 1 is D, we are done, etc.

54 Now comes the backtrack part: In our hypothetical flight plan, there are cities where no flights leave at all(!) If we reach such a city, then we have to return to the previous choice and make another selection. For that I need to store the previous selection, and that is what the stack is used for. Invariant: The stack contains at every moment the cities on a trip from O to the current city. O is at the bottom of the stack. By popping off the top element, I can return to the previous city. After I popped a city off the stack, how do I make sure that I don’t go there again? That’s where the “visited” array is used.

55 Important notes: 1. The described search algorithm does not define at all in what order we are visiting cities. In practice we use the order in the adjacency list. 2. The resultant path might be a very bad one. There might exist a direct flight, and I might choose a much longer path instead. 3. The result will, however, never contain a circle. The “visited” array protects me from that. Now comes the basic algorithm.

56 search(O, D) S. Push(O); visited[O] = TRUE; while ((!S. Stack. Is. Empty( ))&& (S. Get. Stack. Top( ) != D) { C 1 = S. Get. Stack. Top( ); if (/*there are no flights from C 1 to any unvisited city*/) S. Pop( ); else // select any unvisited neighbor C of C 1 S. Push(C); visited[C] = TRUE } } Example: In the previous map, how do we get from P to Z? We start with a stack containing P. As before, the top is at the right. S= P

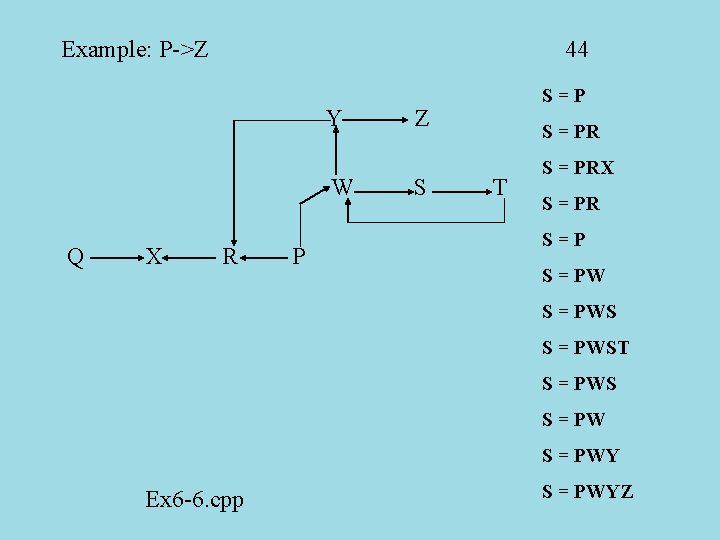
Example: P->Z 44 Y W Q X R P S=P Z S S = PR T S = PRX S = PR S=P S = PWST S = PWS S = PWY Ex 6 -6. cpp S = PWYZ

58 The relationship between stacks and recursion: We could have solved the same search problem in a recursive manner. In fact, this is always true. A recursive program can be modeled by a program using a stack. There is a deeper reason for this: The INTERNAL IMPLEMENTATION of recursion in C++ uses a stack.

59 Recursive. Search(O, D) visited[O] = TRUE if (O == D) // report success else for ( C = all neighbors of O ) Recursive. Search(C, D) Note that this is very rough. The FOR loop would go on after we already were successful.

Summary • ADT stack operations have a last-in, firstout (LIFO) behavior • Stack applications – Algorithms that operate on algebraic expressions – Flight maps • A strong relationship exists between recursion and stacks 60