Lecture 6 Introduction to Algebra RigidBody Motion Allen

Lecture 6 Introduction to Algebra & Rigid-Body Motion Allen Y. Yang September 18 th, 2006 MASKS © 2004 Invitation to 3 D vision
Outline • Euclidean space 1. Points and Vectors 2. Cross products 3. Singular value decomposition (SVD) • Rigid-body motion 1. Euclidean transformation 2. Representation 3. Canonical exponential coordinates 4. Velocity transformations MASKS © 2004 Invitation to 3 D vision

Euclidean space n Points and vectors are different! n Bound vector & free vector: MASKS © 2004 Invitation to 3 D vision

Linear space n The set of all free vectors, V, forms a linear space over the field R. (points don’t) n Closed under “+” and “*” n V is completely determined by a basis, B: n Change of basis: MASKS © 2004 Invitation to 3 D vision

Change of basis Summary: MASKS © 2004 Invitation to 3 D vision
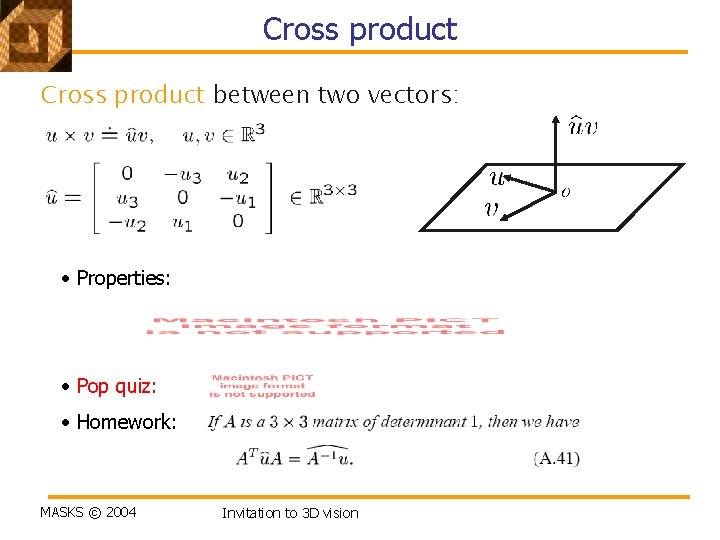
Cross product between two vectors: • Properties: • Pop quiz: • Homework: MASKS © 2004 Invitation to 3 D vision

Rank R is a rotation matrix, T is nontrivial. Pop Quiz: rank( )=? MASKS © 2004 Invitation to 3 D vision

Singular Value Decomposition (SVD) MASKS © 2004 Invitation to 3 D vision

Fixed-Rank Approximation MASKS © 2004 Invitation to 3 D vision

Geometric Interpretation A MASKS © 2004 Invitation to 3 D vision

Rigid-Body Motion n n To describe an object movement, one should specify the trajectory of all points on the object. For rigid-body objects, it is sufficient to specify the motion of one point, and the local coordinate axes attached at it. MASKS © 2004 Invitation to 3 D vision

Rigid-Body Motion n n Rigid-body motions preserve distances, angles, and orientations. Goal: finding representation of SE(3). n Translation T n Rotation R MASKS © 2004 Invitation to 3 D vision

Rotation Orthogonal change of coordinates Collect coordinates of one reference frame relative to the other into a matrix R MASKS © 2004 Invitation to 3 D vision

Degree of Freedom (DOF) n n Translation T has 3 DOF. Rotation R has 3 DOF. Can be specified by three space angles. Summary: R in SO(3) has 3 DOF. g in SE(3) has 6 DOF. Homogeneous representation MASKS © 2004 Invitation to 3 D vision

Homogeneous representation (summary) n Points n Vectors n Transformation n Representation MASKS © 2004 Invitation to 3 D vision

Canonical Exponential Coordinates MASKS © 2004 Invitation to 3 D vision

Canonical Exponential Coordinates n n n One such solution: Yet the solution is NOT unique! when w is a unit vector. Multiplication: MASKS © 2004 Invitation to 3 D vision

Canonical Exponential Coordinates Canonical exponential coordinates for rigid-body motions. Similar to rotation: n (twist) n Hence, MASKS © 2004 Invitation to 3 D vision

Canonical Exponential Coordinates Twist coordinates Velocity transformations Given MASKS © 2004 Invitation to 3 D vision

Summary MASKS © 2004 Invitation to 3 D vision
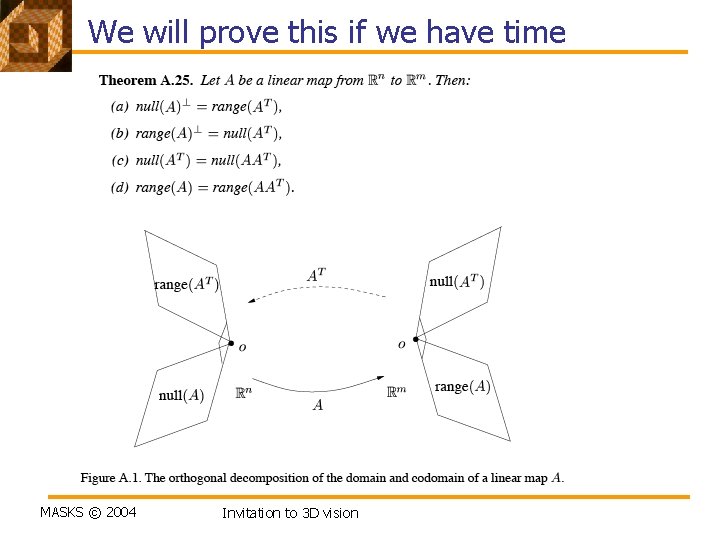
We will prove this if we have time MASKS © 2004 Invitation to 3 D vision
- Slides: 21