Lecture 6 Greedy Algorithms Basic Algorithm Design Techniques

Lecture 6 Greedy Algorithms

Basic Algorithm Design Techniques • Divide and conquer • Dynamic Programming • Greedy • Common Theme: To solve a large, complicated problem, break it into many smaller sub-problems.

Greedy Algorithm • If a problem requires to make a sequence of decisions, for the first decision, make the “best” choice given the current situation. • (This automatically reduces the problem to a smaller sub-problem which requires making one fewer decisions)

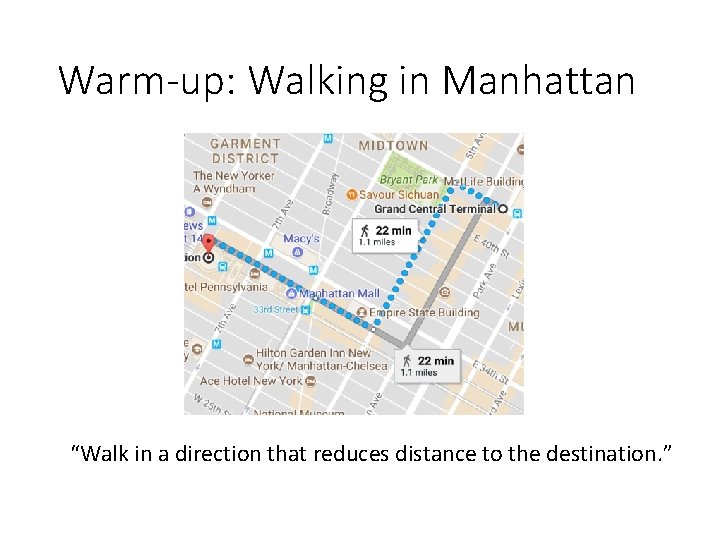
Warm-up: Walking in Manhattan “Walk in a direction that reduces distance to the destination. ”

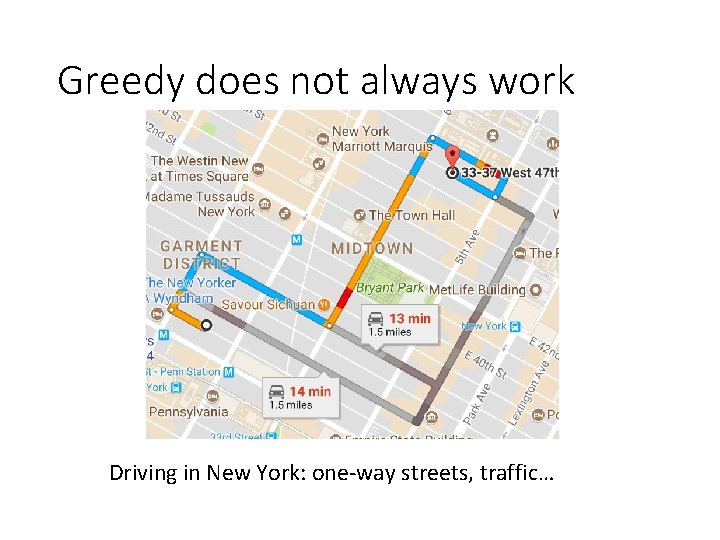
Greedy does not always work Driving in New York: one-way streets, traffic…

Design and Analysis • Designing a Greedy Algorithm: • 1. Break the problem into a sequence of decisions. • 2. Identify a rule for the “best” option. • Analyzing a Greedy Algorithm: • Important! Often fails if you cannot find a proof. • Technique: Proof by contradiction. Assume there is a better solution, show that it is actually not better than what the algorithm did.

Fractional Knapsack Problem • There is a knapsack that can hold items of total weight at most W. There are now n items with weights w 1, w 2, …, wn. Each item also has a value v 1, v 2, …, vn. • The items are infinitely divisible: can put ½ (or any fraction) of an item into the knapsack. • Goal: Select fractions p 1, p 2, …, pn such that • Capacity constraint: p 1 w 1+p 2 w 2+…+pnwn <= W • Maximum Value: p 1 v 1+p 2 v 2+…+pnvn maximized.

Example • Capacity W = 10, • 3 items with (weight, value) = (6, 20), (5, 15), (4, 10) • Solution: Item 1 + 0. 8 Item 2. • Weight = 10, Value = 32

Interval Scheduling • There are n meeting requests, meeting i takes time (si, ti) • Cannot schedule two meeting together if their intervals overlap. • Goal: Schedule as many meetings as possible. • Example: Meetings (1, 3), (2, 4), (4, 5), (4, 6), (6, 8) • Solution: 3 meetings ((1, 3), (4, 5), (6, 8))