Lecture 6 Factors affecting rate of reaction Temperature

Lecture 6. Factors affecting rate of reaction. Temperature and light quantum Prepared by Ph. D Falfushynska H.

Stage plan 1. The Arrhenius Postulations 2. Collisions Theory and Molecular orientations 3. Van-Hoff Rule. 4. How to find the “Activation Energy” 5. Types of photochemical reactions

The Arrhenius Postulations 1903 Nobel Prize citation” …in recognition of the extraordinary services he has rendered to the advancement of chemistry by his electrolytic theory of dissociation” 3

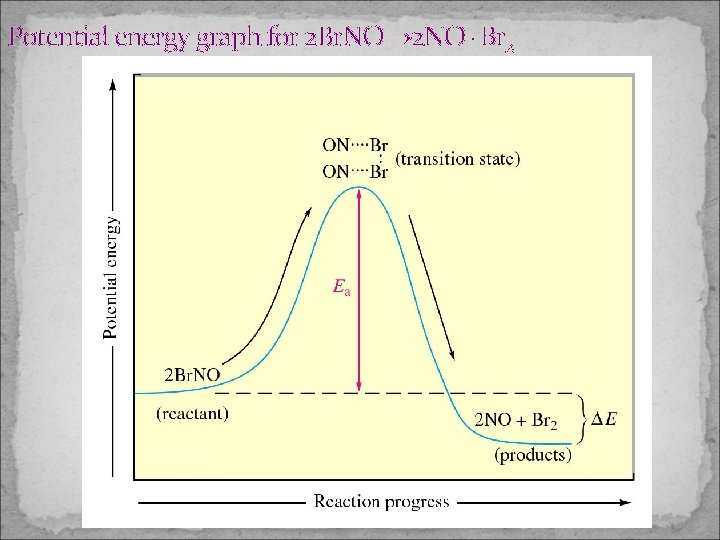
Arrhenius Postulations Collisions and Rate －the rate of reaction is much smaller than calculated collision frequency. A threshold energy (activation energy) －This kinetic energy is changed into potential energy as the molecules are distorted during a collision, breaking bonds and rearranging the atoms into product molecules.

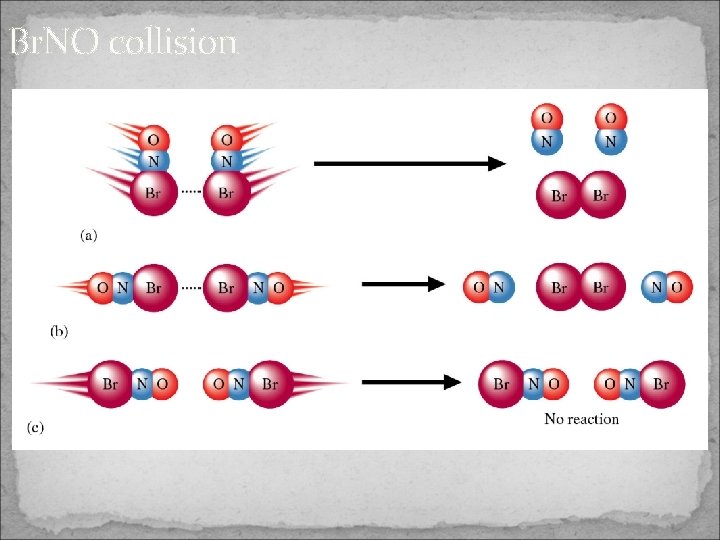
Collisions Theory and Molecular orientations Particles must collide before a reaction can take place Not all collisions lead to a reaction: Experiments show that the observed reaction rate is considerably smaller than the rate of collisions with enough energy to surmount the barrier. The collision must involve enough energy to produce the reaction – Activation energy. The relative orientation of the reactants must allow formation of any new bonds necessary to products. – Steric effect

Br. NO collision

Potential energy graph for 2 Br. NO→ 2 NO+Br 2

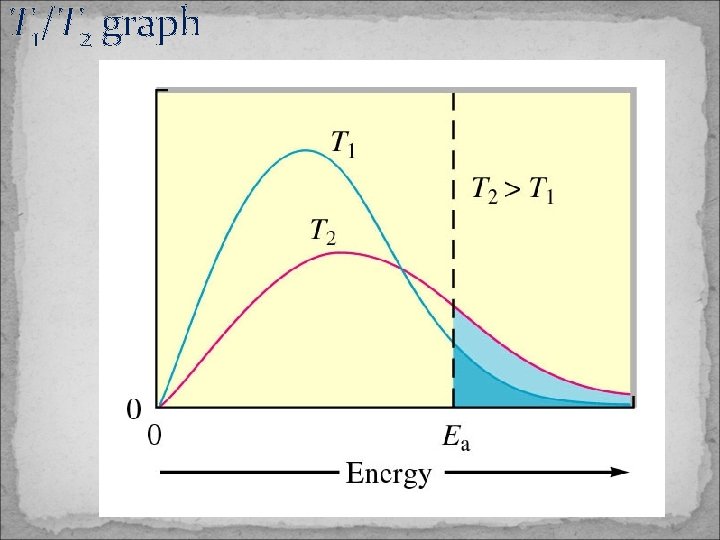
Temperature Dependence of Rate Constants The order of each reactant depends on the detailed reaction mechanism. Chemical reaction speed up when the temperature is increased. －molecules must collide to react －an increase in temperature increases the frequency of intermolecular collisions.

T 1/T 2 graph

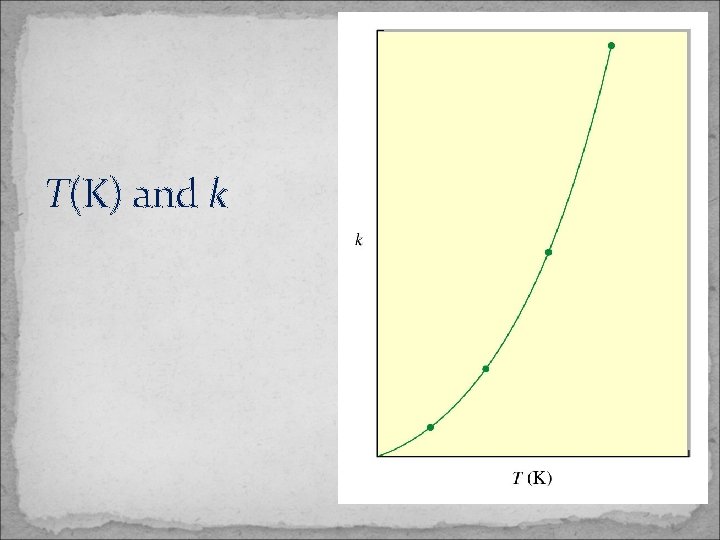
T(K) and k

Temperature and Rate The Arrhenius Equation • Arrhenius discovered most reaction-rate data obeyed the Arrhenius equation: ln k = ln A – Ea / R T – k is the rate constant, Ea is the activation energy, R is the gas constant (8. 3145 J K-1 mol-1) and T is the temperature in K. – A is called the frequency factor. – A is a measure of the probability of a favorable collision. – Both A and Ea are specific to a given reaction.

Application of Arrhenius Equation From k = A e – Ea / R T, calculate A, Ea, k at a specific temperature and T. The reaction: 2 NO 2(g) -----> 2 NO(g) + O 2(g) The rate constant k = 1. 0 e-10 s-1 at 300 K and the activation energy Ea = 111 k. J mol-1. What are A, k at 273 K and T when k = 1 e-11? k = A e – Ea / R T A=ke Ea / R T A/k=e Ea / R T ln (A / k) = Ea / R T

Application of Arrhenius Equation The reaction: 2 NO 2(g) -----> 2 NO(g) + O 2(g) The rate constant k = 1. 0 e-10 s-1 at 300 K and the activation energy Ea = 111 k. J mol-1. What are A, k at 273 K and T when k = 1 e-11? Use the formula derived earlier: A = k e. Ea / R T = 1 e-10 s-1 exp (111000 J mol-1 / (8. 314 J mol-1 K – 1*300 K)) = 2. 13 e 9 s-1 k = 2. 13 e 9 s-1 exp (– 111000 J mol-1) / (8. 314 J mol-1 K – 1*273 K) = 1. 23 e-12 s-1 T = Ea / [R* ln (A/k)] = 111000 J mol-1 / (8. 314*46. 8) J mol-1 K-1 = 285 K 13

Van-Hoff Rule: If t 2 t 1 Temperature coefficient:

Drug Stability testing by method of accelerating ageing :

Stability testing and calculation of shelf-life The shelf-life for the product can be calculated from the rate constant based on an acceptable degree of decomposition. The time taken for 10% loss of activity is given by t 90 = 0. 105/k 1 The Arrhenius equation is used as the basis of a method for accelerating decomposition by raising the temperature of the preparations. 1. Determination of the order of reaction by plotting stability data at several elevated temperatures according to the equations relating decomposition to time for each of the orders of reaction, until linear plots are obtained.

Values of the rate constant k at each temperature are calculated from the gradient of these plots, and the logarithm of k is plotted against reciprocal temperature according to the Arrhenius equation log k = log A – Ea/2. 303 RT. A value of k can be interpolated from this plot at the required temperature. where k 1 and k 2 are the rate constants at temperatures T 1 and T 2 respectively. A mid-range value of Ea = 75 k. J mol– 1 may be used for these rough estimation

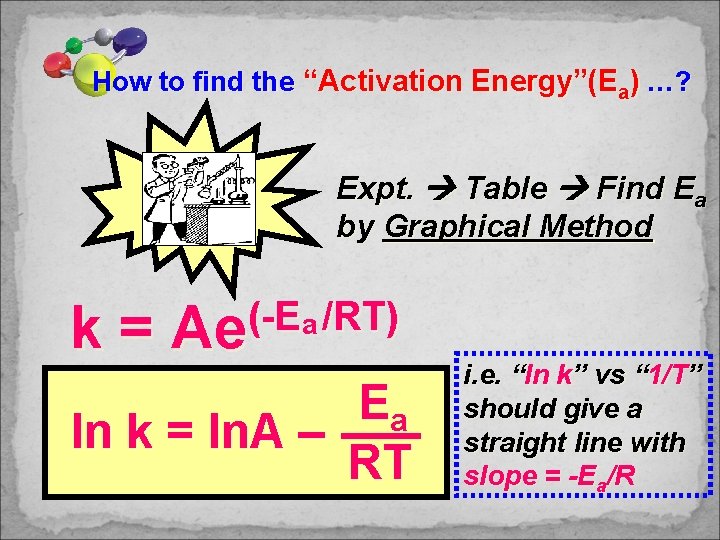
How to find the “Activation Energy”(Ea) …? Expt. Table Find Ea by Graphical Method k= (-E /RT) a Ae Ea ln k = ln. A – RT i. e. “ln k” vs “ 1/T” should give a straight line with slope = -Ea/R

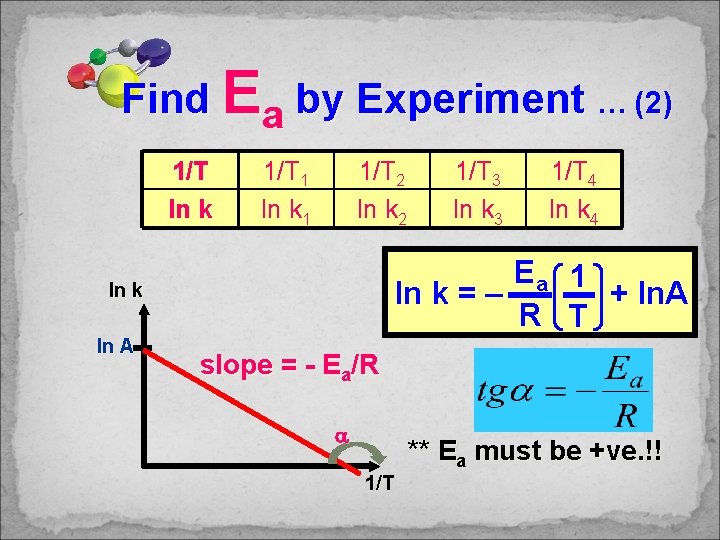
Find Ea by Experiment … (1) At T 1, find “k 1” by Differential / Integrated Rate Eqn At T 2, find “k 2” by Differential / Integrated Rate Eqn T k T 1 k 1 T 2 k 2 T 3 k 3 T 4 k 4 1/T ln k 1/T 1 ln k 1 1/T 2 ln k 2 1/T 3 ln k 3 1/T 4 ln k 4

Find Ea by Experiment … (2) 1/T ln k 1/T 1 ln k 1 1/T 2 ln k 2 Ea ln k = – R ln k ln A 1/T 3 ln k 3 1/T 4 ln k 4 1 + ln. A T slope = - Ea/R 1/T ** Ea must be +ve. !!

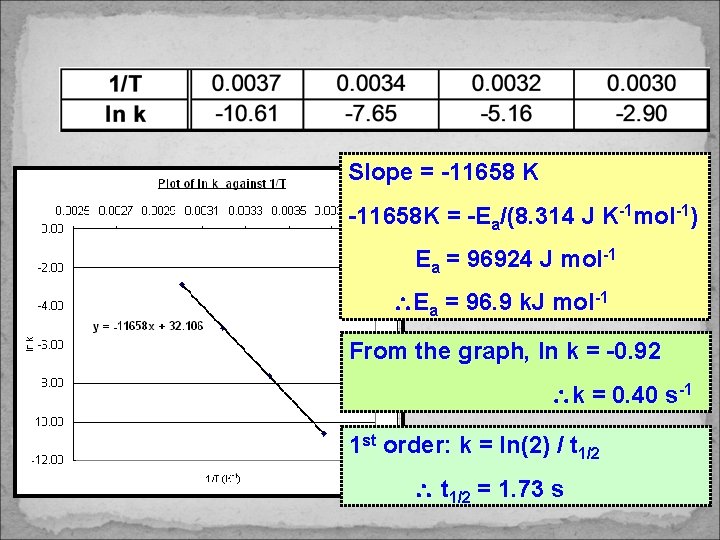
Slope = -11658 K -11658 K = -Ea/(8. 314 J K-1 mol-1) Ea = 96924 J mol-1 Ea = 96. 9 k. J mol-1 From the graph, ln k = -0. 92 k = 0. 40 s-1 1 st order: k = ln(2) / t 1/2 = 1. 73 s

Mechanisms of Light Absorption Excitation: A bonding electron is lifted to a higher energy level (higher orbital)

INTERACTION OF LIGHT AND MATERIALS: a) X 2* → X 2 + M* (excess energy transferred to the surrounding) b) X 2* → X 2 + hn (fluorescence or phosphorescence) c) X 2* + Y → chemical reaction (excess energy supplies the activation energy of the reaction)

Types of photochemical reactions a) Photodissociation b) Photosynthesis: when a larger molecule is formed from simple ones c) Photosensitized reactions: when an excited molecule supplies activation energy for the reactants (energy of the photon supplies the „dissociation heat”)

Photodissociation Photolysis of hydrogen bromide Overall:

Note: 1 photon absorbed, 2 molecules of HBr dissociated:

Ozone formation in the atmosphere (at about 25 km altitude) Notes: M absorbs energy released in the reaction

Photosynthesis. The photosynthesis of hydrogen chloride Note: Quantum yield is about 106 (explosion)

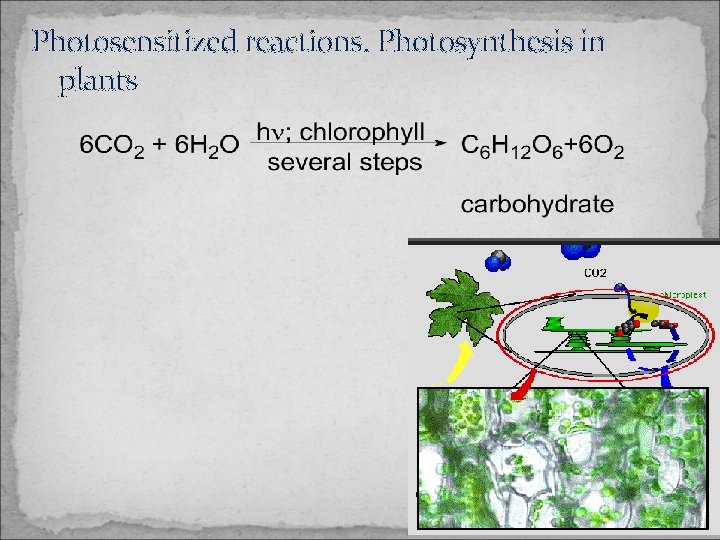
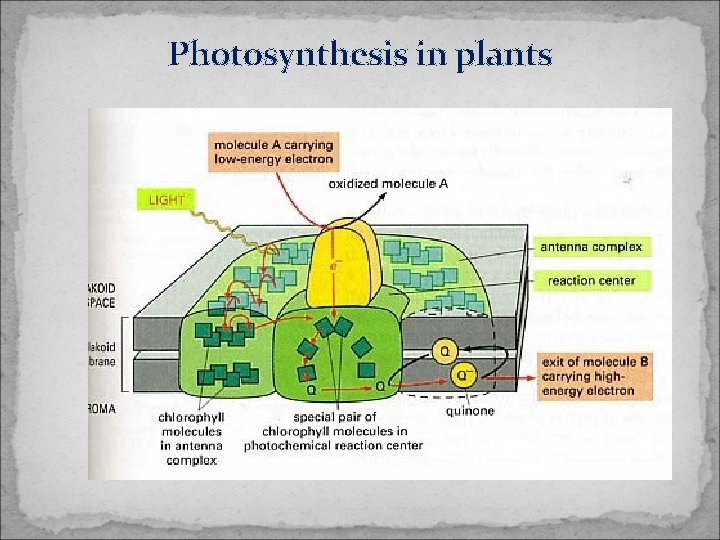
Photosensitized reactions. Photosynthesis in plants

Photosynthesis in plants

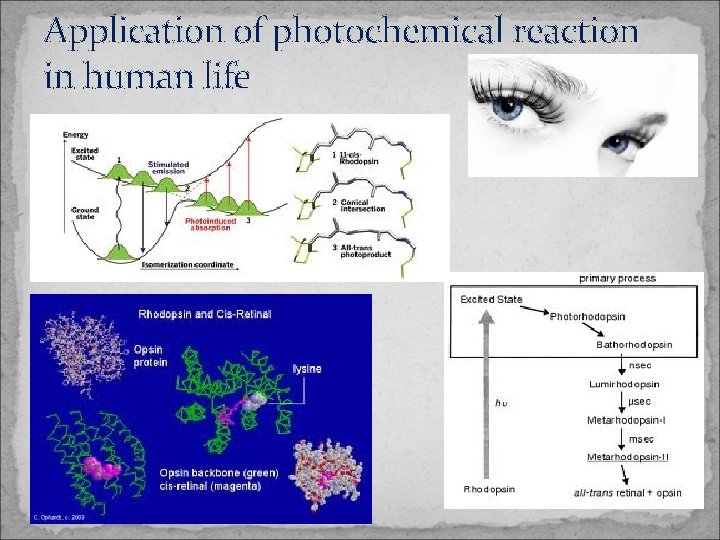
Application of photochemical reaction in human life

Non-Rotating Annular Photochemical Reactor # Large Quartz immersion well. # 400 watt medium pressure mercury lamp. # Reactor base and carousel assembly (non rotating), including support rod and immersion well adjustable clamp. # set of sample tube support rings for eight 25 mm sample tubes # Only the inner or the outer tubes may be irradiated effectively at one time # UV Screen: - consisting of three black coated aluminum sections. A light tight lid, a removable front and back section, that are joined by means of a light tight seal