Lecture 6 Dynamic Programming 01 Knapsack Making Change

Lecture 6: Dynamic Programming 0/1 Knapsack Making Change (any coin set)

What is Dynamic Programming? Dynamic programming is similar to divide-and-conquer in that the problem is broken down into smaller subproblems. In this approach we solve the small instances first, save the results, and look them up later when we needed, rather than recompute them. 1. establish a recursive property that gives the solution to an instance of the problem 2. solve instances of the problem in a bottom-up fashion starting with the smaller instances first. Dynamic programming can sometimes provide an efficient solution to a problem for which divide-and-conquer produces an exponential run-time. Occasionally we find that we do not need to save all subproblem solutions. In these cases we can revise the algorithm greatly reducing the memory space requirements for the algorithm.

Binomial Theorem The binomial theorem gives a closed-form expression for the coefficient of any term in the expansion of a binomial raised to the nth power. (a+b)0 = 1 (a+b)1 = a+b (a+b)2 = a 2+2 ab+b 2 (a+b)3 = a 3+3 a 2 b+3 ab 2+b 3 (a+b)4 = a 4+4 a 3 b+6 a 2 b 2+4 ab 3+b 4

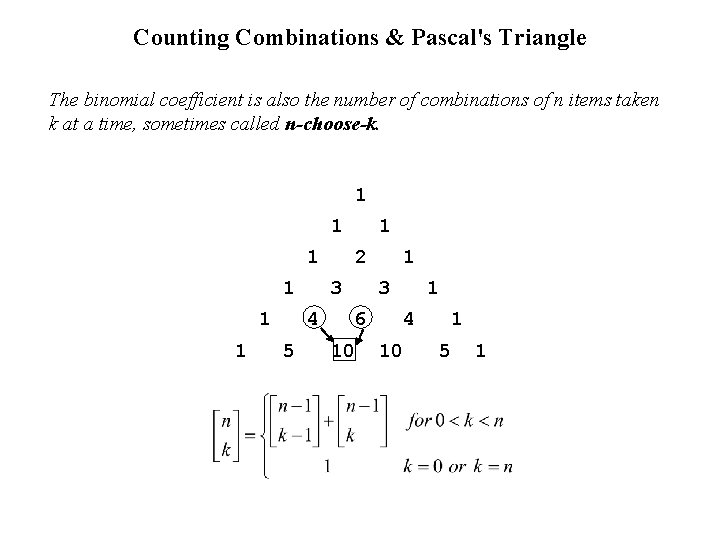
Counting Combinations & Pascal's Triangle The binomial coefficient is also the number of combinations of n items taken k at a time, sometimes called n-choose-k. 1 1 1 1 2 3 3 4 5 1 6 1 10 4 10 1 5 1

Binomial Coefficient D&C Version function bin(n, k : integer) return integer is begin if k=0 or k=n then return 1; else return bin(n-1, k-1) + bin(n-1, k); end if; end bin; This version of bin requires that the subproblems are recalculated many times for each recursive call.

Binomial Coefficient Dynamic Programming function bin 2(n, k: integer) return integer s B : array(0. . n, o. . k) of integer; begin for i in 0. . n loop for j in 0. . minimum(i, k) loop if j=0 or j=i then B(i, j)=1; else B(i, j): =B(i-1, j-1) + B(i-1, j); end if; end loop; return B(n, k); end bin 2; In bin 2 the smallest instances of the problem are solved first and then used to compute values for the larger subproblems. Compare the computational complexities of bin and bin 2.

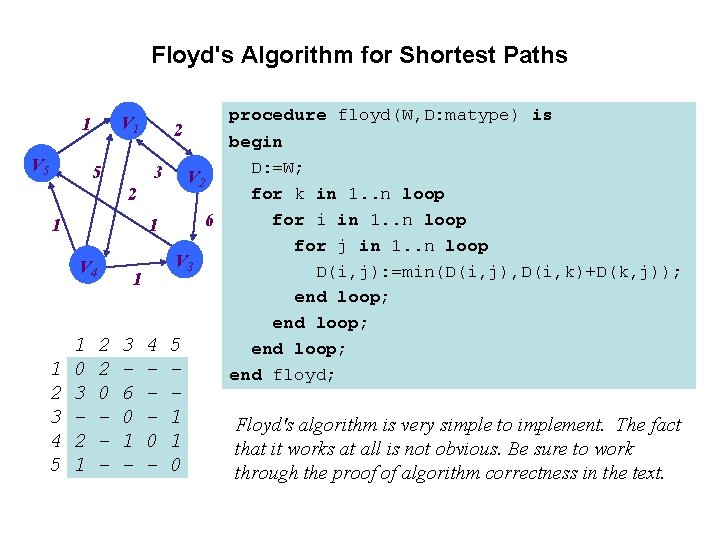
Floyd's Algorithm for Shortest Paths V 1 1 V 5 5 2 3 2 1 1 V 4 1 2 3 4 5 1 0 3 2 1 1 2 2 0 - 3 6 0 1 - 4 0 - procedure floyd(W, D: matype) is begin D: =W; V 2 for k in 1. . n loop for i in 1. . n loop 6 for j in 1. . n loop V 3 D(i, j): =min(D(i, j), D(i, k)+D(k, j)); end loop; 5 end loop; end floyd; 1 1 0 Floyd's algorithm is very simple to implement. The fact that it works at all is not obvious. Be sure to work through the proof of algorithm correctness in the text.

Dynamic Programming - The Coin Changing Problem Northeastern University - Javed A. Aslam - CSG 713 Advanced Algorithms

Defining the Recurrence Relation Northeastern University - Javed A. Aslam - CSG 713 Advanced Algorithms

Implementing the Bottom-Up Algorithm Northeastern University - Javed A. Aslam - CSG 713 Advanced Algorithms

Generating an Optimal Solution Northeastern University - Javed A. Aslam - CSG 713 Advanced Algorithms

Algorithm/Program Analysis Northeastern University - Javed A. Aslam - CSG 713 Advanced Algorithms

Summary Dynamic Programming solves problems that can be expressed as recurrence relations Rather than recursive programming (e. g. D&C) Dyn. Pro solves these problem in a bottom-up fashion It is good practice to compare complexity for D&C vs Dyn. Pro works when sub-problems are solved by sub-solutions. That is, optimal partial solutions are parts of the optimal solution.