Lecture 6 Delays and Timing in Multilevel Logic

Lecture 6 Delays and Timing in Multilevel Logic Synthesis Prith Banerjee ECE C 03 Advanced Digital Design Spring 1998 ECE C 03 Lecture 6 1

Outline • • • Gate delays Timing waveforms Performance calculations Static/dynamic hazards and glitches Designs to avoid hazards READING: Katz 3. 3, 3. 4, 3. 5. 2, Dewey 6. 5. 1, 6. 5. 2 ECE C 03 Lecture 6 2

Time Response in Combinational Networks • emphasis on timing behavior of circuits • waveforms to visualize what is happening • simulation to create these waveforms • momentary change of signals at the outputs: hazards can be useful— pulse shaping circuits can be a problem — glitches: incorrect circuit operation Terms: gate delay— time for change at input to cause change at output minimum delay vs. typical/nominal delay vs. maximum delay careful designers design for the worst case! rise time— time for output to transition from low to high voltage fall time— time for output to transition from high to low voltage ECE C 03 Lecture 6 3

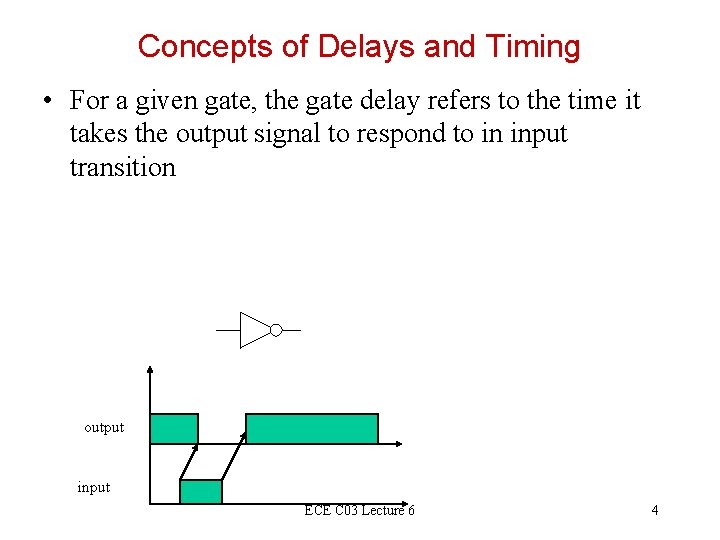
Concepts of Delays and Timing • For a given gate, the gate delay refers to the time it takes the output signal to respond to in input transition output input ECE C 03 Lecture 6 4

Gate Delays • Why is there a gate delay? • There actual resistances and capacitances inside digital logic • If you apply a unit step voltage signal to an input, the output will not respond immediately, but after a delay proportional to R. C T delay = R. C Resistance of driver Input Capacitance of load Output ECE C 03 Lecture 6 5

Delays in Combinational Logic Input transition Output transition QUESTION: After the input goes from low to high how long does it take for the output to go from low to high (note depends on other inputs being 1 or 0) ANSWER: Use simple delay models for each gate and add up delays in a path from input to output ECE C 03 Lecture 6 6

Delays in Combinational Logic Wire load Capacitance C Delay (nsec) Low drive High drive Load capacitance (p. F) ECE C 03 Lecture 6 7

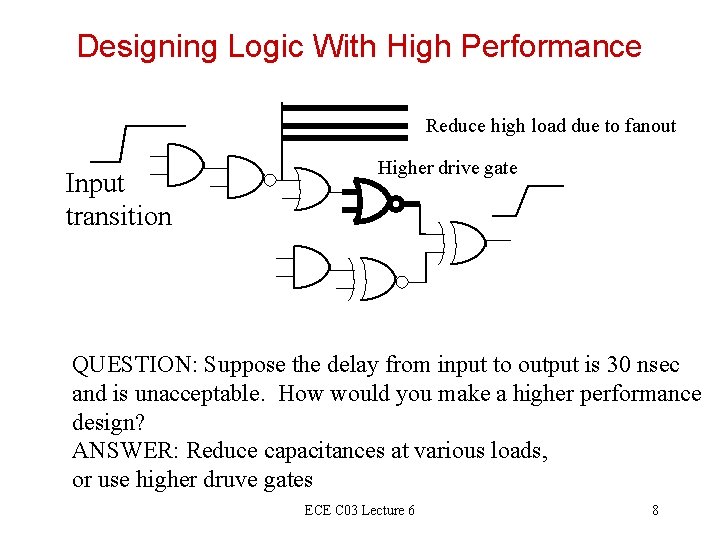
Designing Logic With High Performance Reduce high load due to fanout Input transition Higher drive gate QUESTION: Suppose the delay from input to output is 30 nsec and is unacceptable. How would you make a higher performance design? ANSWER: Reduce capacitances at various loads, or use higher druve gates ECE C 03 Lecture 6 8

Gate Delays for Typical TTL Families Delays in nano-seconds ECE C 03 Lecture 6 9

Gate Delay Specifications Example gate delays in nanoseconds for LSI Logic 1. 5 micron gate array 2 input AND gate. tp. LH = Propagation delay from low to high transition at output tp. HL = Propagation delay from high to low transition at output ECE C 03 Lecture 6 10

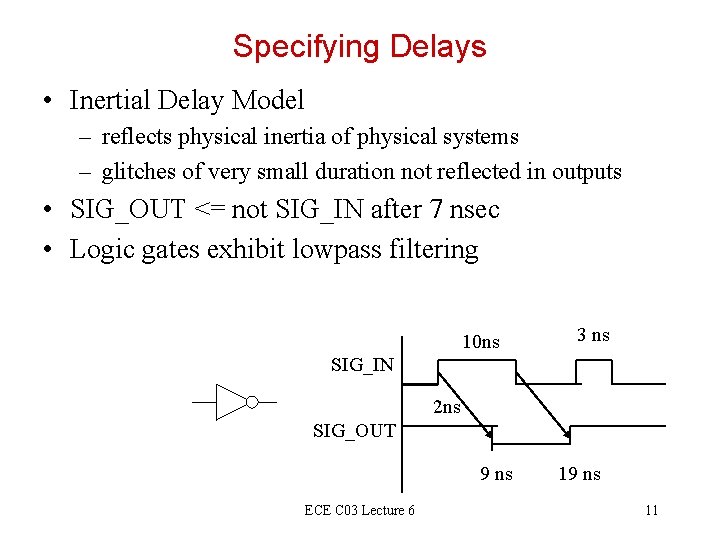
Specifying Delays • Inertial Delay Model – reflects physical inertia of physical systems – glitches of very small duration not reflected in outputs • SIG_OUT <= not SIG_IN after 7 nsec • Logic gates exhibit lowpass filtering 10 ns 3 ns SIG_IN 2 ns SIG_OUT 9 ns ECE C 03 Lecture 6 19 ns 11

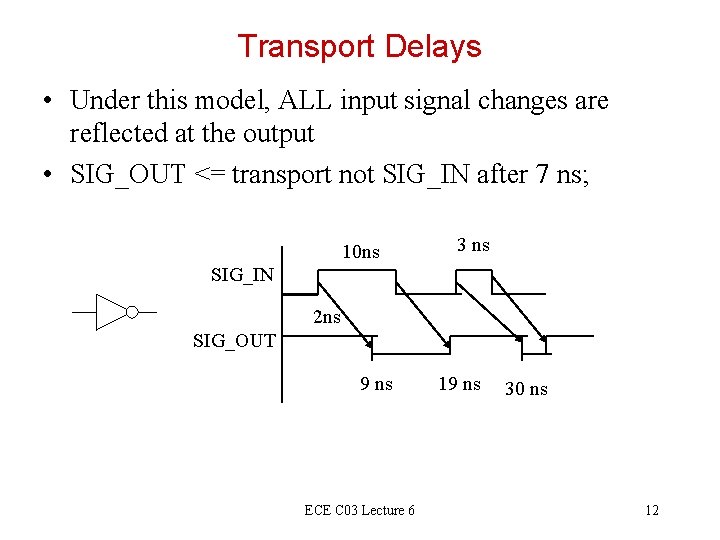
Transport Delays • Under this model, ALL input signal changes are reflected at the output • SIG_OUT <= transport not SIG_IN after 7 ns; 10 ns 3 ns SIG_IN 2 ns SIG_OUT 9 ns ECE C 03 Lecture 6 19 ns 30 ns 12

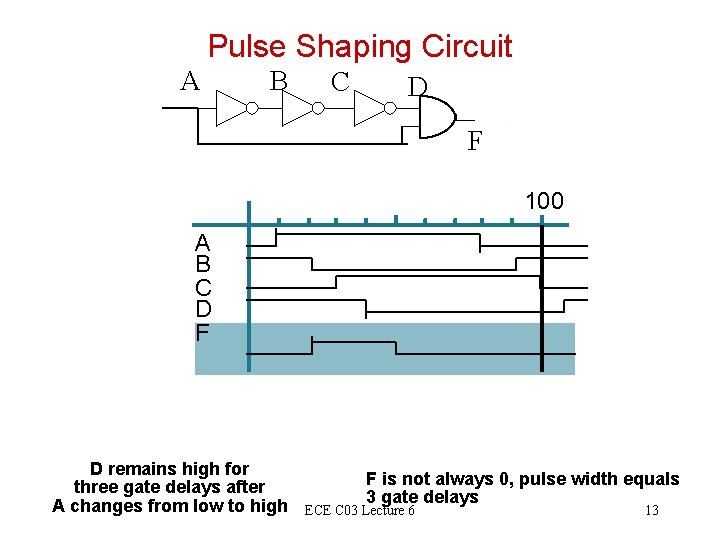
Pulse Shaping Circuit A B C D F 100 A B C D F D remains high for three gate delays after A changes from low to high F is not always 0, pulse width equals 3 gate delays ECE C 03 Lecture 6 13

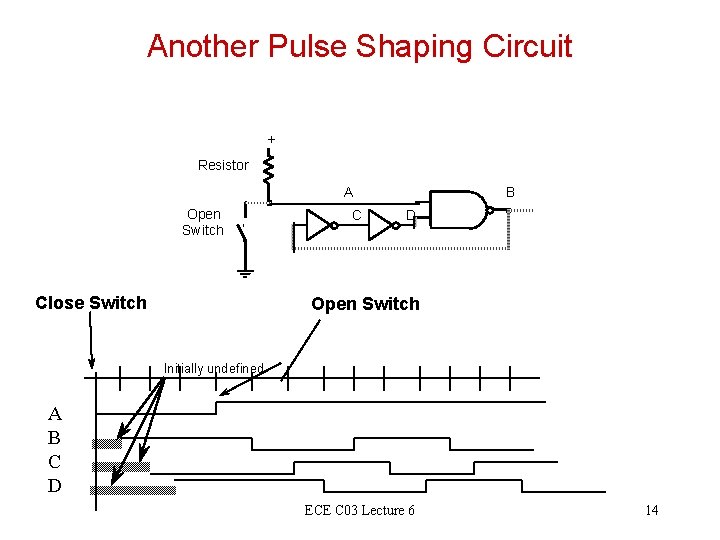
Another Pulse Shaping Circuit + Resistor A Open Switch Close Switch C B D Open Switch Initially undefined A B C D ECE C 03 Lecture 6 14

Hazards and Glitches Unwanting switching at the outputs Occur because delay paths through the circuit experience different propagation delays Danger if logic "makes a decision" while output is unstable OR hazard output controls an asynchronous input (these respond immediately to changes rather than waiting for a synchronizing signal called a clock) Usual solutions: wait until signals are stable (by using a clock) never, never use circuits with asynchronous inputs design hazard-free circuits Suggest that first two approaches be used, but we'll tell you about hazard-free design anyway! ECE C 03 Lecture 6 15

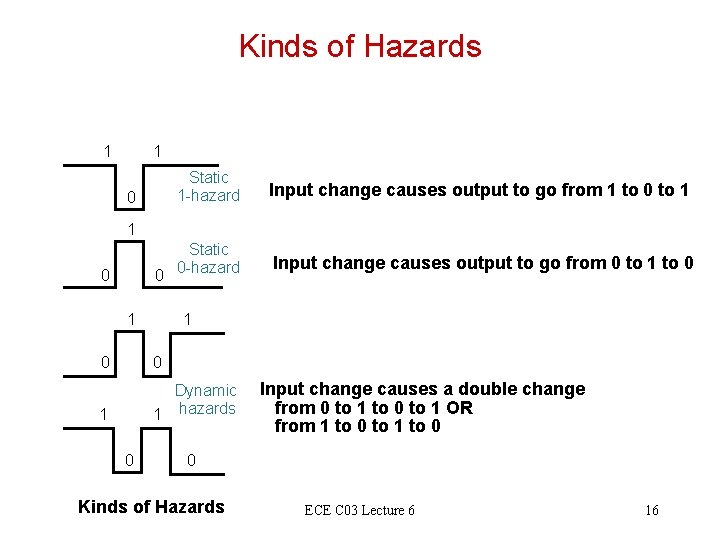
Kinds of Hazards 1 1 Static 1 -hazard Input change causes output to go from 1 to 0 to 1 Static 0 0 -hazard Input change causes output to go from 0 to 1 to 0 0 1 1 0 0 1 Dynamic 1 hazards 0 Input change causes a double change from 0 to 1 to 0 to 1 OR from 1 to 0 to 1 to 0 0 Kinds of Hazards ECE C 03 Lecture 6 16

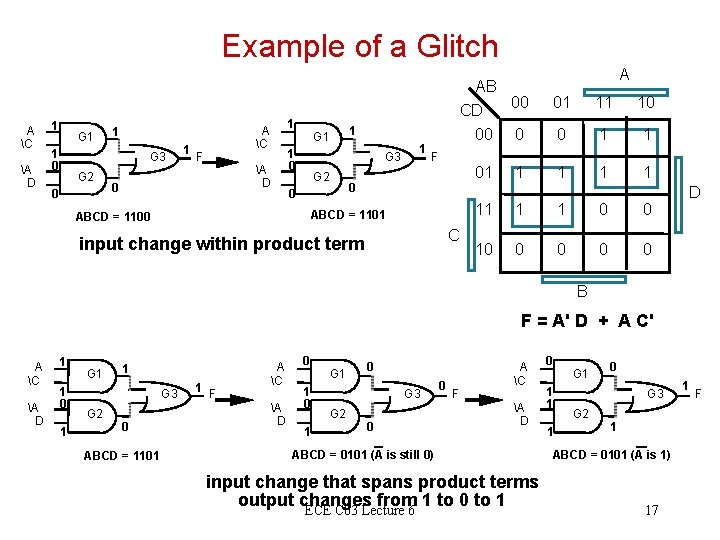
Example of a Glitch A C A D 1 G 1 1 0 G 3 G 2 0 1 1 A C 1 F A D 0 1 G 1 1 0 G 3 G 2 1 F 01 01 11 10 0 1 1 1 0 0 D ABCD = 1101 ABCD = 1100 A AB 00 CD 00 0 C input change within product term 11 1 1 0 0 10 0 0 B F = A' D + A C' A C A D 1 1 0 1 G 3 G 2 A C 1 0 ABCD = 1101 1 F A D 0 1 G 1 0 G 3 G 2 0 0 A C F A D ABCD = 0101 (A is still 0) input change that spans product terms output changes from 1 to 0 to 1 ECE C 03 Lecture 6 0 G 1 1 1 0 G 3 G 2 1 1 ABCD = 0101 (A is 1) 17 1 F

Eliminating Glitches General Strategy: add redundant terms F = A' D + A C' becomes A' D + A C' + C' D This eliminates 1 -hazard? How about 0 -hazard? AB 00 CD 00 0 Re-express F in Po. S form: F = (A' + C')(A + D) 01 Glitch present! 1 A 01 11 10 0 1 1 1 D Add term: (C' + D) C This expression is equivalent to the hazard-free So. P form of F ECE C 03 Lecture 6 11 1 1 0 0 10 0 0 B 18

How to design Circuits without Glitches Start with expression that is free of static 1 -hazards F = A C' + A' D + C' D Work with complement: F' = (A C' + A' D + C' D)' = (A' + D) (A + D') (C + D') = A C + A C D' + A' C D' + A' D' = A C + C D' + A' D' covers all the adjacent 0's in the K-map free of static-1 and static-0 hazards! ECE C 03 Lecture 6 19

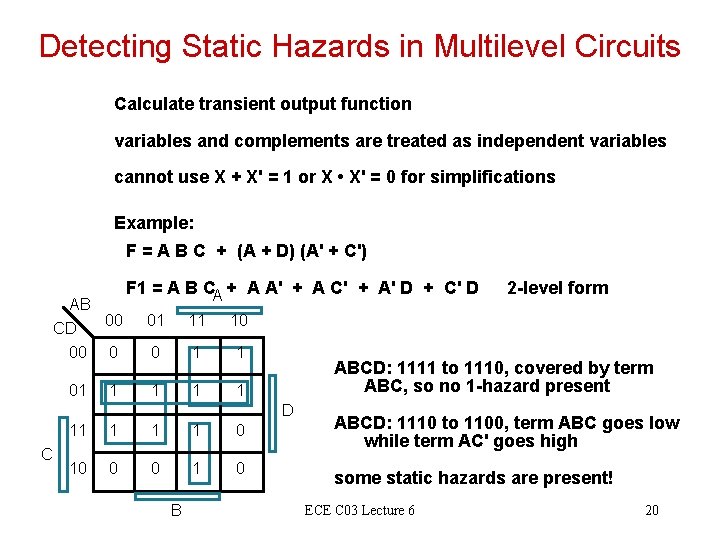
Detecting Static Hazards in Multilevel Circuits Calculate transient output function variables and complements are treated as independent variables cannot use X + X' = 1 or X • X' = 0 for simplifications Example: F = A B C + (A + D) (A' + C') AB 00 CD 00 0 01 1 F 1 = A B C + A A' + A C' + A' D + C' D A 01 11 10 0 1 1 1 ABCD: 1111 to 1110, covered by term ABC, so no 1 -hazard present D C 11 1 0 10 0 0 1 0 B 2 -level form ABCD: 1110 to 1100, term ABC goes low while term AC' goes high some static hazards are present! ECE C 03 Lecture 6 20

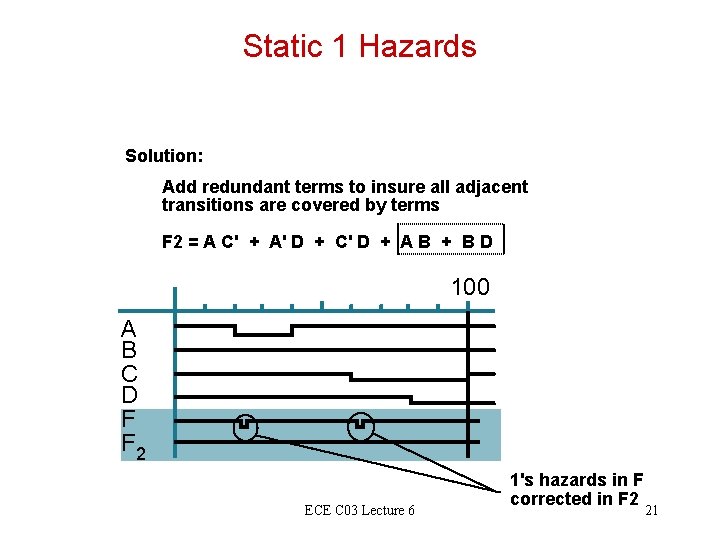
Static 1 Hazards Solution: Add redundant terms to insure all adjacent transitions are covered by terms F 2 = A C' + A' D + C' D + A B + B D 100 A B C D F F 2 ECE C 03 Lecture 6 1's hazards in F corrected in F 2 21

Static 0 Hazards Similar to previous case, but work with the complement of F If terms of the transient output function cover all 0 transitions, then no 0 -hazards are present AB 00 CD 00 0 F = [A B C + (A + D) (A' + C')]' = (A' + B' + C') (A' D' + A C) 01 = A' D' + A' B D' + A' C D' + A B' C = A' D' + A B' C 01 11 10 0 1 1 1 D C + B' C D' 1 A 11 1 0 10 0 0 1 0 B F = (A + D) (A' + B + C') (B + C' + D) 0 -hazard free equivalent to F 2 on last slide ECE C 03 Lecture 6 0 -hazard on transition from 1010 to 0010 22

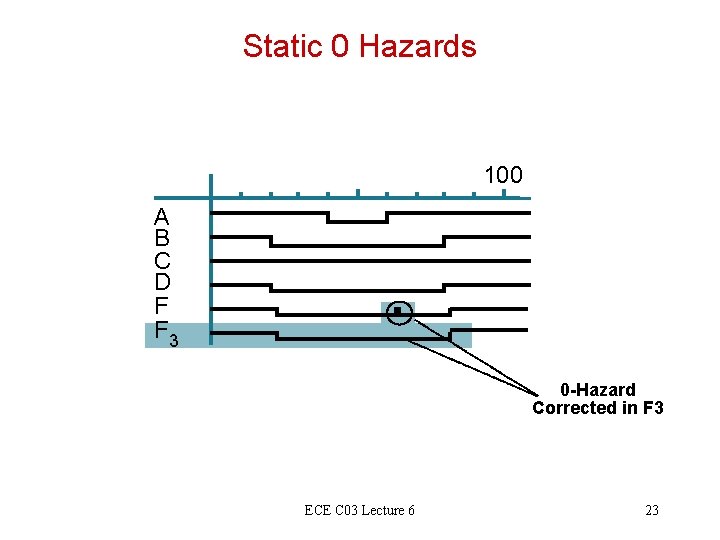
Static 0 Hazards 100 A B C D F F 3 0 -Hazard Corrected in F 3 ECE C 03 Lecture 6 23

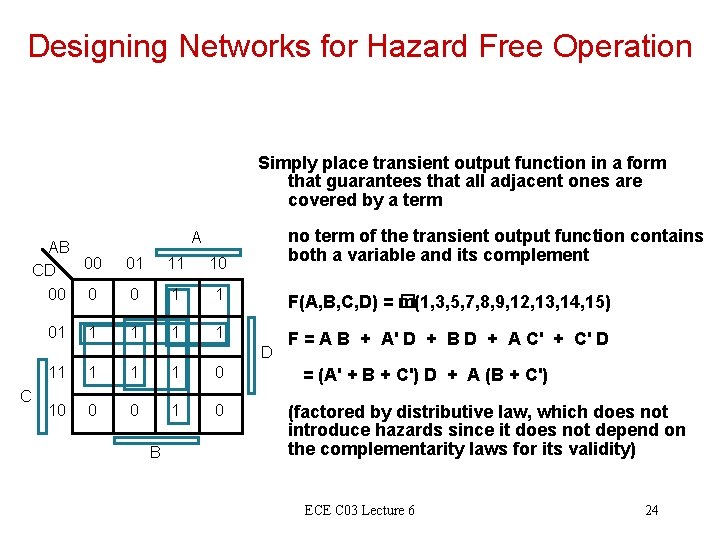
Designing Networks for Hazard Free Operation Simply place transient output function in a form that guarantees that all adjacent ones are covered by a term AB 00 CD 00 0 01 1 A 01 11 10 0 1 1 1 no term of the transient output function contains both a variable and its complement F(A, B, C, D) = � m(1, 3, 5, 7, 8, 9, 12, 13, 14, 15) D C F = A B + A' D + B D + A C' + C' D 11 1 0 = (A' + B + C') D + A (B + C') 10 0 0 1 0 (factored by distributive law, which does not introduce hazards since it does not depend on the complementarity laws for its validity) B ECE C 03 Lecture 6 24

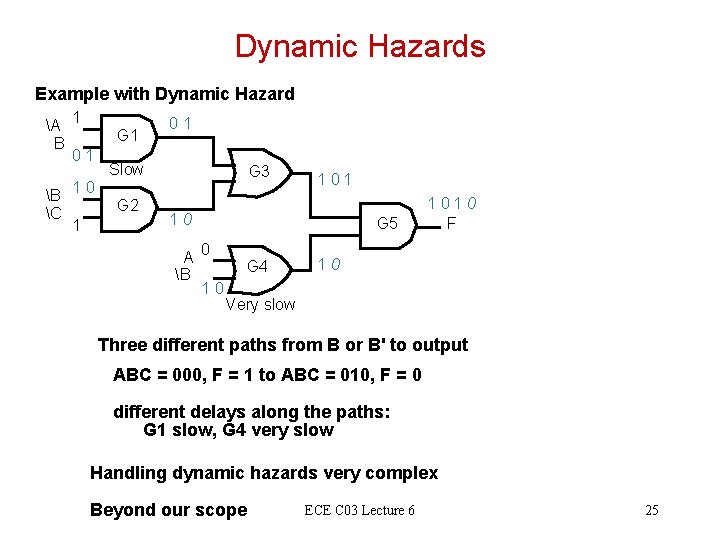
Dynamic Hazards Example with Dynamic Hazard A 1 B 01 B 1 0 C 1 G 1 01 Slow G 2 G 3 1 01 10 A B G 5 0 G 4 10 1 01 0 F 10 V ery slow Three different paths from B or B' to output ABC = 000, F = 1 to ABC = 010, F = 0 different delays along the paths: G 1 slow, G 4 very slow Handling dynamic hazards very complex Beyond our scope ECE C 03 Lecture 6 25

Summary • • Gate delays Timing waveforms Performance calculations Static/dynamic hazards and glitches Designs to avoid hazards NEXT LECTURE: Multilevel Logic Synthesis READING: Katz 3. 1, 3. 2 ECE C 03 Lecture 6 26