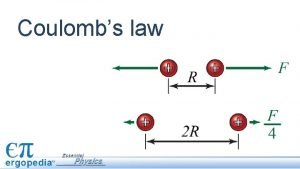
Lecture 6 Ch 21 Coulombs Law University Physics

Lecture 6 Ch 21. Coulomb’s Law University Physics: Waves and Electricity Dr. -Ing. Erwin Sitompul http: //zitompul. wordpress. com 2013

Homework 5: Ambulance Siren An ambulance with a siren emitting a whine at 1600 Hz overtakes and passes a cyclist pedaling a bike at 8 m/s. After being passed, the cyclist hears a frequency of 1590 Hz. (a) How fast is the ambulance moving? (b) What frequency did the cyclist hear before being overtaken by the ambulance? Erwin Sitompul University Physics: Wave and Electricity 6/2

Solution of Homework 5: Ambulance Siren (a) (b) Erwin Sitompul University Physics: Wave and Electricity 6/3

Electric Charge § Static cling, an electrical phenomenon that accompanies dry weather, causes the pieces of paper to stick to one another. This is an example that reveals the existence of electric charge. § In fact, every object contains a vast amount of electric charge. § Electric charge is an intrinsic characteristic of the fundamental particles making up those objects. § The vast amount of charge in an everyday object is usually hidden because the object contains equal amounts of the two kinds of charge: positive charge and negative charge. § With such a balance of charge, the object is said to be electrically neutral (contains no net charge). § If the two types of charge are not in balance, we say that an object is charged, it has a net charge. Erwin Sitompul University Physics: Wave and Electricity 6/4

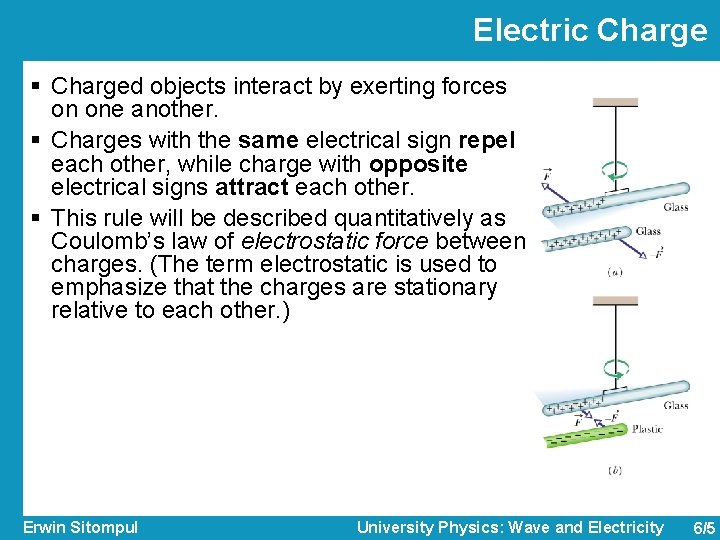
Electric Charge § Charged objects interact by exerting forces on one another. § Charges with the same electrical sign repel each other, while charge with opposite electrical signs attract each other. § This rule will be described quantitatively as Coulomb’s law of electrostatic force between charges. (The term electrostatic is used to emphasize that the charges are stationary relative to each other. ) Erwin Sitompul University Physics: Wave and Electricity 6/5

Coulomb’s Law § If two charged particles are brought near each other, they each exert a force on the other. § If the particles have the same sign of charge, they repel each other. The force on each particle is directed away from the other particle. § If the particles have opposite signs of charge, they attract each other. The force on each particle is directed toward the other particle. Erwin Sitompul University Physics: Wave and Electricity 6/6

Coulomb’s Law § This force of repulsion or attraction due to the charge properties of objects is called an electrostatic force. § The equation giving the force for charged particles is called Coulomb’s law, named after Charles-Augustin de Coulomb, who did the experiments in 1785. § If particle 1 has charge q 1 and particle 2 has charge q 2, the force on particle 2 is: § The term is a unit vector to the direction from position of q 1 to position of q 2. The term k is a constant. Erwin Sitompul University Physics: Wave and Electricity 6/7

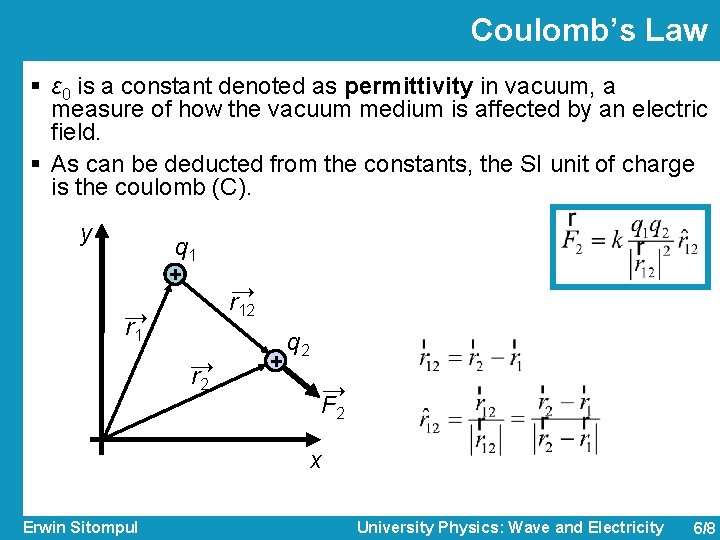
Coulomb’s Law § ε 0 is a constant denoted as permittivity in vacuum, a measure of how the vacuum medium is affected by an electric field. § As can be deducted from the constants, the SI unit of charge is the coulomb (C). y q 1 + r→ 12 → r 1 → r 2 + q 2 → F 2 x Erwin Sitompul University Physics: Wave and Electricity 6/8

Some Examples on Vectors § Example: If , find § Example: If and . , find and . § Both vectors are of opposite direction, but have the same magnitude Erwin Sitompul University Physics: Wave and Electricity 6/9

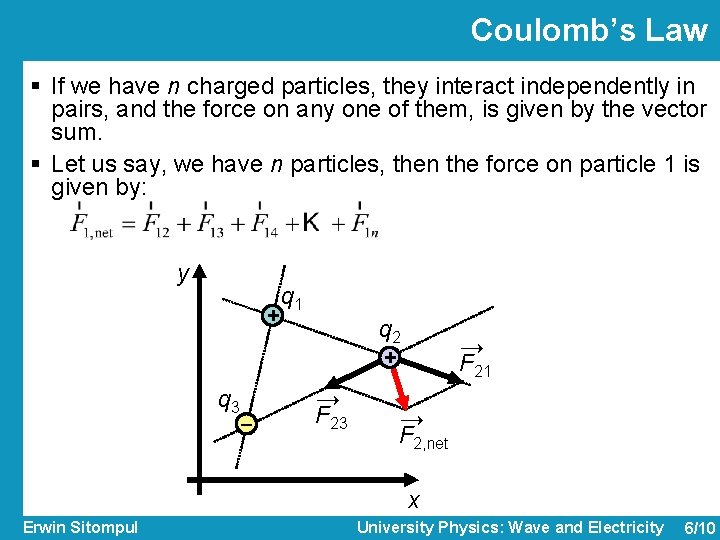
Coulomb’s Law § If we have n charged particles, they interact independently in pairs, and the force on any one of them, is given by the vector sum. § Let us say, we have n particles, then the force on particle 1 is given by: y + q 1 q 2 → F 21 + q 3 – → F 23 → F 2, net x Erwin Sitompul University Physics: Wave and Electricity 6/10

Example 1: Coulomb’s Law The figure below shows two positively charged particles fixed in place on an x axis. The charges are q 1 = 1. 6 10– 19 C and q 2 = 3. 2 10– 19 C. The q 1 is located on the origin, while the separation is R = 0. 02 m. What are the magnitude and direction of the electrostatic force → F 12 on particle 1 from particle 2? Erwin Sitompul University Physics: Wave and Electricity 6/11

Example 2: Coulomb’s Law Now, particle 3 lies on the x axis between particles 1 and 2. Particle 3 has charge q 3 = – 3. 2 10– 19 C and is at a distance 3/4 R from particle 1. → What is the net electrostatic force F 1, net on particle 1 due to particles 2 and 3? Erwin Sitompul University Physics: Wave and Electricity 6/12

Example 3: Coulomb’s Law Particle 3 from previous example is now replaced by particle 4. Particle 4 has charge q 4 = – 3. 2 10– 19 C, is at a distance 3/4 R from particle 1, and lies on a line that makes an angle θ = 60° with the x axis. → What is the net electrostatic force F 1, net on particle 1 due to particles 2 and 4? Erwin Sitompul University Physics: Wave and Electricity 6/13

Example 3: Coulomb’s Law Erwin Sitompul University Physics: Wave and Electricity 6/14

Checkpoint The figure below shows three arrangements of one electron (e) and two protons (p). (a) Rank the arrangements according to the magnitude of the net electrostatic force on the electron due to the protons, largest first a, c, b (b) In situation c, is the angle between the net force on the electron and the line labeled d less than or more than 45 °? Less than 45° Erwin Sitompul University Physics: Wave and Electricity 6/15

Example 4: Coulomb’s Law Two particles are fixed in place: a particle of charge q 1 = +8 q at the origin and a particle of charge q 2 = – 2 q at x = L. At what point can a particle of charge q 3 = +4 q be placed so that it is in equilibrium (the net force on q 3 is zero)? → → F 32 F 31 : impossible to place q 3 on the left of q 1 or in the middle between q 1 and q 2 : the only possibility is to place q 3 to the right-hand side of q 2 Erwin Sitompul → F 32 → F 31 University Physics: Wave and Electricity 6/16

Example 4: Coulomb’s Law • q 3 between q 1 and q 2 • q 3 to the right of q 2 Charge q 3 must be placed on the x axis, at distance L to the right of q 3, or, at point (2 L, 0) Erwin Sitompul → F 32 L x University Physics: Wave and Electricity → F 31 6/17

Charge Is Quantized § Experiment shows that electric charge is not continuous but is made up of multiples of a certain elementary charge (quantized). § Any positive or negative charge q that can be detected can be written as in which e, the elementary charge, has the approximate value § The elementary charge e is one of the important constants of nature. The electron and proton both have a charge of magnitude e. Erwin Sitompul University Physics: Wave and Electricity 6/18

Exercise Problems 1. Three point charges are arranged along the xaxis. Charge q 1 = +3 μC is at the origin, and the charge q 2 = – 5 μC is at x = 0. 2 m. Charge q 3 = – 8 μC. Where is q 3 located if the net force on q 1 is 7 N in the negative x-direction? Answer: x = – 0. 144 m. 2. Two point charges are located on an xy-plane as follows. The first charge, q 1 = 2 μC is located at (2, 4). The second charge, q 2 = – 3 μC is located at → (1, 6). Determine the force vector acting on q 2, i. e. F 21. ^ ^ → Answer: F 21 = 4. 824 i – 9. 649 j m. N Erwin Sitompul University Physics: Wave and Electricity 6/19