Lecture 6 ANALYSIS AND SYNTHESIS OF COMBINATIONAL CIRCUITS

Lecture 6: ANALYSIS AND SYNTHESIS OF COMBINATIONAL CIRCUITS. • ANALYSIS AND DESIGN 1 PROCEDURE. • BINARY ADDERS • BINARY SUBTRACTOR.

INTRODUCTION q Logic circuits for digital systems may be combinational or sequential. q A combinational circuits consist of logic gates whose out puts at any time are determined directly from the present combination of current inputs without regard to past inputs. q A sequential circuit employ memory elements in addition to logic gates (i. e. output is function of present and previous inputs). 2

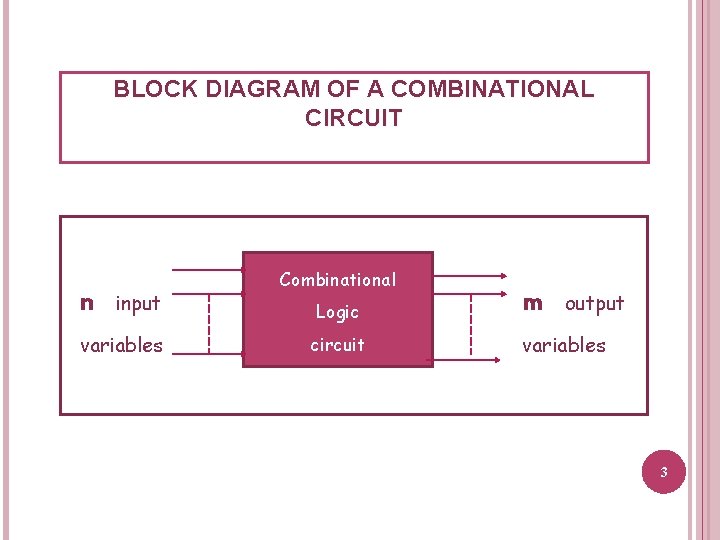
BLOCK DIAGRAM OF A COMBINATIONAL CIRCUIT n input variables Combinational Logic circuit m output variables 3

DESIGN PROCEDURE The procedure involves the following steps : 1. The problem is started. 2. The number of available input variables and required output variables is deter – mined. 3. The input and output variables are assigned letter symbols. 4. The truth table that defines the required relationships between inputs and outputs is derived. 5. The simplified Boolean function for each output is obtained. 6. The logic diagram is drawn. 4

ADDERS Digital computers perform a variety of information processing tasks. Among the basic functions the arithmetic addition is the most basic operation. 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 5

HALF ADDER The circuit has 2 inputs and 2 outputs X Y C S 0 0 0 1 1 0 S=x'y+xy'=x C=xy y+ 6

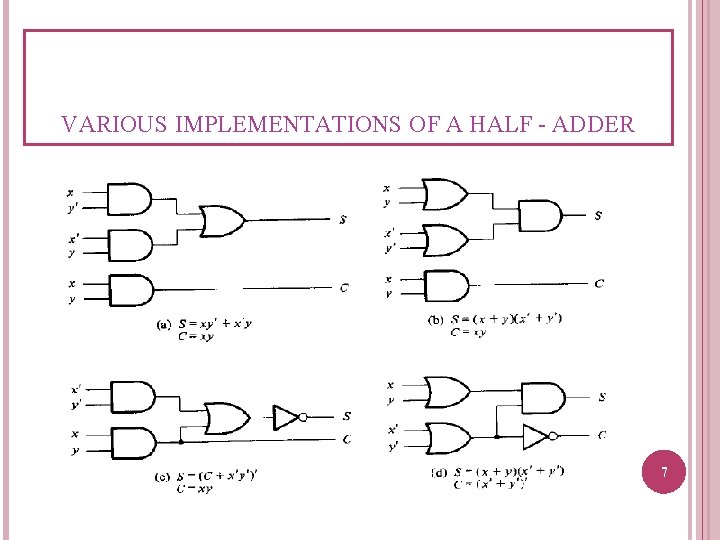
VARIOUS IMPLEMENTATIONS OF A HALF - ADDER 7

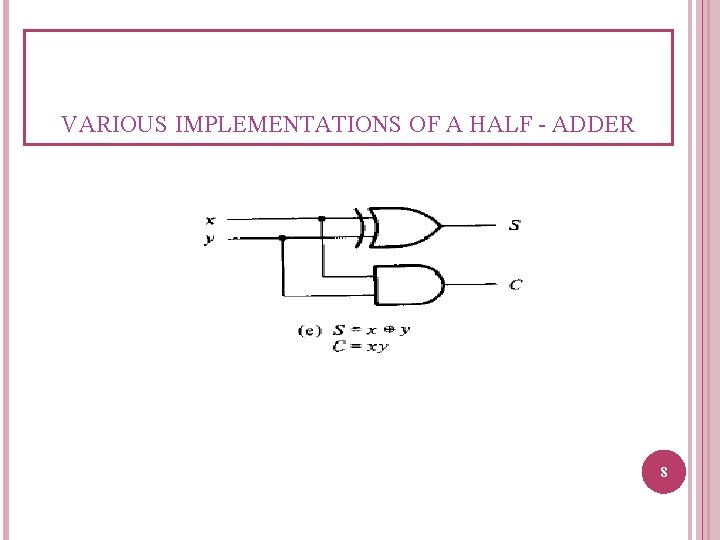
VARIOUS IMPLEMENTATIONS OF A HALF - ADDER 8

Full Adder The circuit has 3 inputs two of them are the 2 numbers to be added the third is the Cin carry input from the previous stage and 2 outputs the sum and carry out Cout. 9

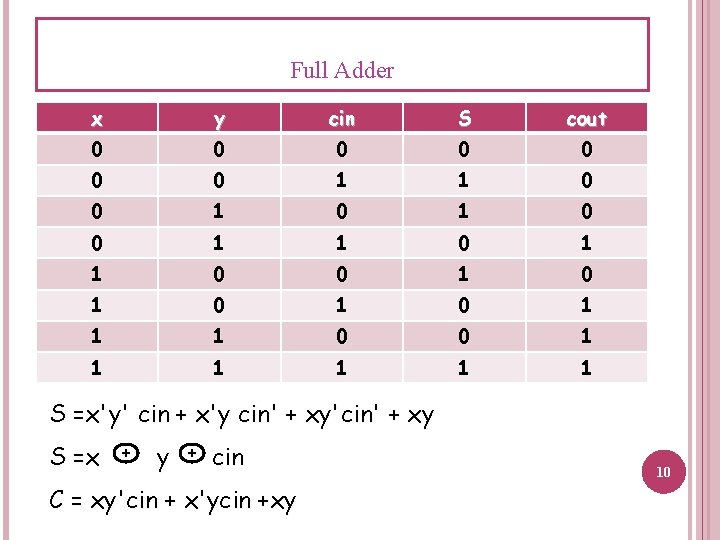
Full Adder x y cin S cout 0 0 0 0 1 1 0 0 1 0 1 1 1 0 0 1 1 1 S =x'y' cin + x'y cin' + xy'cin' + xy S =x + y + cin C = xy'cin + x'ycin +xy 10

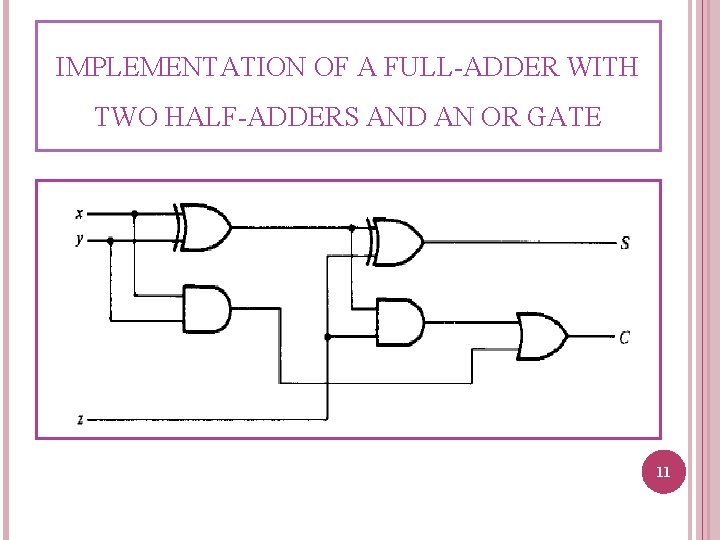
IMPLEMENTATION OF A FULL-ADDER WITH TWO HALF-ADDERS AND AN OR GATE 11

SUBTRACTORS The subtraction of two binary numbers may be accomplished by taking the complement of the subtrahend adding it to the minuend 12

HALF-SUBTRACTOR X Y B D 0 0 0 1 1 1 0 0 D= x'y + xy' B= x'y 13

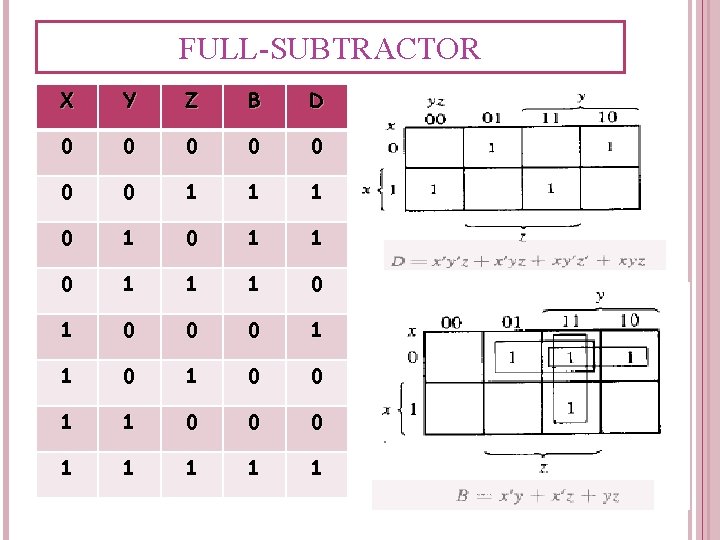
FULL-SUBTRACTOR X Y Z B D 0 0 0 0 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 14