Lecture 6 Activity Scales and Activity Corrections Learn

Lecture 6 Activity Scales and Activity Corrections Learn how to make activity corrections Free ion activity coefficients Debye Huckel Equations Mean Salt Method Ion Complexation (% Free) Total Activity Coefficients Major Ion Speciation of SW

Definition: Concentration (ci) = total concentration Activity (ai) = effective concentration In very dilute solutions: ai = ci In seawater ai < ci

Two main reasons for activity corrections 1. Electrostatic Interactions Dilute Solutions Seawater A general electrostatic shielding

2. Ion Complexing ion pairs and complexes example: Ca 2+ + SO 42 = Ca. SO 4 ligands: Cl , SO 42 , HCO 32 , CO 32 Specific new species form specific ion interactions

Activity Coefficient The total concentration of an element (m. T). First: we need to convert the total concentration (m. T) to the concentration of the ion or species (mi). In order to calculate mi from m. T we need to do an equilibrium calculation of the percent free which we express as fi. Thus: mi = m T fi Example: For the case where we have Ca. T but we want Ca 2+ we need to calculate the ratio: f. Ca 2+ = [Ca 2+]/ Ca. T = [Ca 2+] / ([Ca 2+]+ [Ca. SO 4 ]+ [Ca. HCO 3+] + [Ca. CO 3 ])

Second: Convert concentration of the free ion (mi) to the activity of the free ion (ai). Use the free ion activity coefficient ( i) that corrects for electrostatic shielding This correction is written as: ai = i mi molal concentration of a free ion activity coefficient for that species The total expression with both correction factors is then written as: ai = i fi m. T is the total ion concentration % of the total concentration, m. T, that is free Sometimes i and fi are combined together and called the total activity coefficient, T. Where, the total activity coefficient = T = i fi Then: ai = T m. T

Example: a solution with Ca 2+ , SO 42 and CO 32 forms the complexes Ca. SO 4 , Ca. HCO 3 and Ca. CO 3 T, Ca = fi Ca 2+ = ([Ca 2+]/ Ca. T) Ca 2+ = ([Ca 2+ ] / ([Ca 2+ ]+ [Ca. SO 4 ] + [Ca. HCO 3+] + [Ca. CO 3 ])) Ca 2+

How do we obtain values for i and fi. 1. i Free Ion Activity Coefficient The free ion activity coefficient describes the relation between the activity and concentration of a free ion species. We use either some form of the Debye Huckel type equations or the mean salt method 2. fi % free ==== We obtain this from a chemical speciation calculation done by hand or using a computer program like MINTEQA 2 or HYDRAQL.

Ionic Strength I I = 1/2 S mi • Zi 2 charge of i th ion concentration of i th ion The ionic strength has concentration units. Example: . Na+ Mg 2+ Ca 2+ K+ Cl SO 42 HCO 3 Molality Seawater (SW) Lake Water (LW) 0. 49 0. 2 x 10 3 0. 053 0. 14 x 10‑ 3 0. 010 0. 22 x 10 3 0. 010 0. 03 x 10 3 0. 57 0. 09 x 10 3 0. 028 0. 102 x 10 3 0. 002 0. 816 x 10 3 ISW = 1/2 (m. Na x 12 + m. Mg x 22 + m. Ca x 22 + m. K x 12 + m. Cl x 12 + m. SO 4 x 22 + m. HCO 3 x 12) = 0. 72 mol kg 1 ILW = 0. 0015 = 1. 5 x 10 3 mol kg‑ 1 ISW = 500 x I FW.

Debye Huckel Equations: (based on theory) Limiting Law Extended D H I = ionic strength log i = A zi 2 I 1/2 applicable for I < 10 -2 log i = -A zi 2 I 1/2 / (1 + ai • B • I 1/2 ) for I < 10 -1 ai = ion size parameter A = 0. 51 at 25 C B = 0. 33 x 108 Davies Equation log i = -A zi 2 {I 1/2 / (1 + I 1/2 ) - 0. 2 I} ; for I < 0. 5 (almost seawater) monovalent ions = i = 0. 69 divalent ions = i = 0. 23 trivalent ions = i = 0. 04 All ions of the same charge have same γ Assumption is that ai · B = 1 in extended D-H

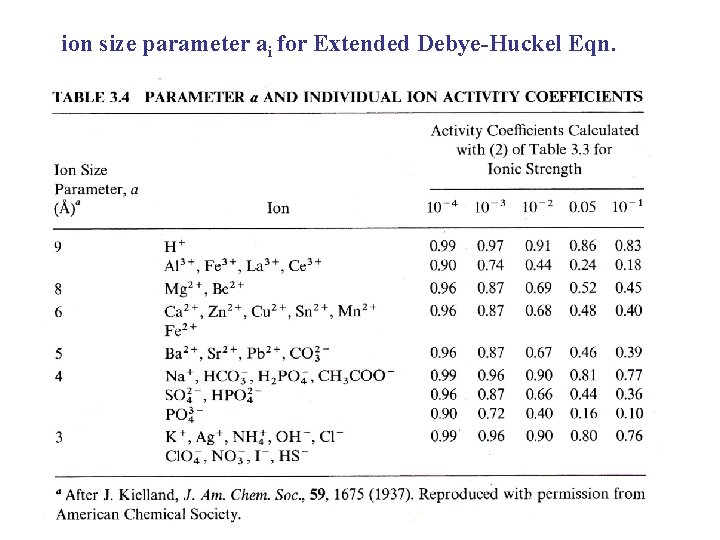
1. f in this table is the same as γ 2. a is called the ion size parameter

ion size parameter ai for Extended Debye Huckel Eqn.

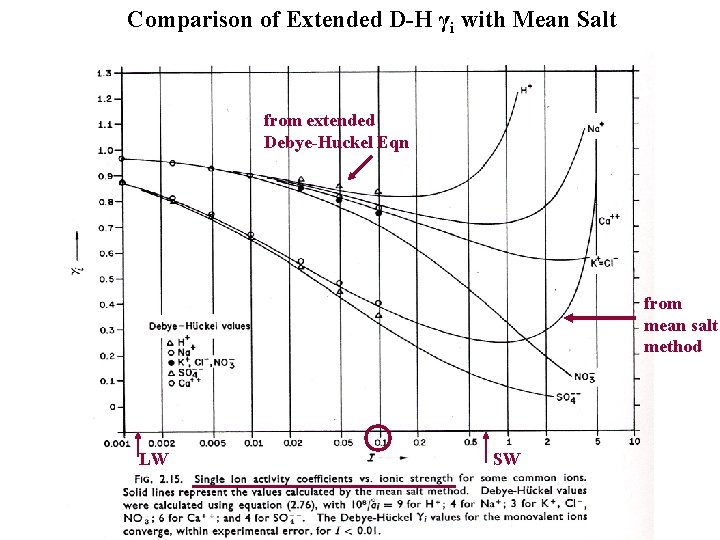
Comparison of Extended D H γi with Mean Salt from extended Debye Huckel Eqn from mean salt method LW SW

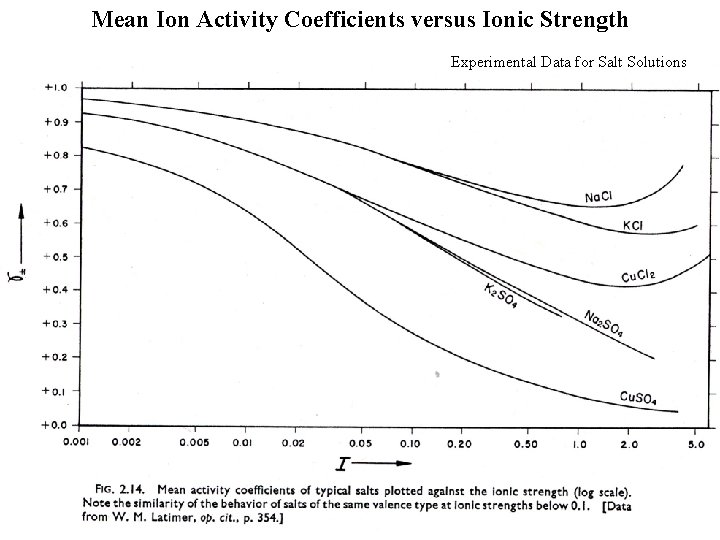
Mean Salt Method (based on data) This is an empirical method that uses the experimental determinations of mean ion activity coefficients ( +). This mean is the geometric mean: +Na. Cl = Na+ • Cl Usually such data are obtained by measuring the deviation from ideality of the colligative properties of solutions (e. g. osmotic pressure, vapor pressure of water). Explain! Activity coefficients are always measured on salt solutions which contain both cations and anions. The mean value is reported which is expressed as the geometric mean ( ) as given below for a generic salt MCl. The Mean Activity Coefficients for typical salts are plotted against Ionic Strength in the next figure

Mean Ion Activity Coefficients versus Ionic Strength Experimental Data for Salt Solutions

We need the values of the individual ion activity coefficients (e. g. M+ ). Use the Mac. Innes Assumption KCl = K+ = Cl , If MCl = [ M+. Cl ] 1/2 where M+ is any singly charged cation we replace (e. g. Cl ) with the mean activity coefficient for KCl (e. g. KCl). = [ M+. KCl ]1/2 Thus: M+ = ( MCl )2 / KCl See values for ions plotted in Figure with Extended D H values.

General Rules for Free Ion activity Coefficients (see slide 13) 1. i 1 as I 0 i. e. activity = concentration at infinite dilution 2. i as I i. e. , the free ion activity coefficient decreases with ionic strength 3. 2+ < + i. e. , the activity corrections decrease with increasing charge 4. i at high I Called the salting out effect. 5. There is good agreement between mean salt method and Extended Debye Huckel equation to I = 0. 1. 6. Rules of Thumb for free ion activity coefficients in seawater. When stuck for an answer use the following values. ion charge range +1 0. 6 to 0. 8 avg = 0. 7 +2 0. 1 to 0. 3 avg = 0. 2 +3 0. 01 +4 < 0. 01

Solution Speciation % Free Ion Pairs have all the properties of dissolved species: 1. Their dissociation reactions have equilibrium constants 2. Ion pairs have their own individual ion activity coefficients ( i) Here are some general rules: 1. higher the charge on an ion the greater the complexing 2. higher the concentration of complexing ions the greater the complexing 3. ignore higher order complexes species formed from 3 or more ions, e. g. Ca(HCO 3)2 4. Cl ion pairs are very weak and can be ignored. 5. +3 and higher ions (e. g. Fe 3+) form strong hydroxyl (OH ) complexes. Hydrolysis. 6. many organic compounds tend to form strong complexes with TM.

Example: Speciation of a Ca 2+, CO 32 , HCO 3 , SO 42 solution Imagine a solution with one cation and three anions: Ca 2+, CO 32 , HCO 3 and SO 42 Ca 2+ can form complexes with all three anions and we can write their dissociation reactions as: Ca. CO 3º Ca 2+ + CO 32 Ca. HCO 3+ Ca 2+ + HCO 3 Ca. SO 4º Ca 2+ + SO 42 We need the concentrations of 4 chemical species: one free ion and three complexes, We have 4 unknowns. Assumes we know the concentrations of CO 32 , HCO 3 and SO 42. To solve for 4 unknown concentrations we need 4 equations: 1) One equation is the mass balance or sum of the concentrations of the four species: Ca. T == [Ca 2+] + [Ca. CO 3 ] + [Ca. HCO 3 ] + [Ca. SO 4 ] 2) Three equations are the equilibrium constants formation of the complexes. e. g. KCa. CO 3 = (Ca 2+)(CO 32 ) / (Ca. CO 3 ) = [Ca 2+] Ca 2+ [CO 3 2 ] CO 3 / [Ca. CO 3 ] Ca. CO 3 These are all free ion activity coefficients. We can solve this equation for the concentration of [Ca. CO 3 ] = [Ca 2+] Ca 2+ [CO 32 ] CO 3 / KCa. CO 3

Substitute the K's for the three complexes in the mass balance we obtain one equation: Ca. T == [Ca 2+] + [Ca 2+] Ca 2+ [CO 3 2 ] CO 3 / KCa. CO 3 + [Ca 2+] Ca 2+ [HCO 3 ] HCO 3 / KCa. HCO 3 + [Ca 2+] Ca 2+ [SO 42 ] SO 4 / KCa. SO 4 What information do we need? 1) the values for the three equilibrium constants, K 2) The free ion activity coefficients for the free ions e. g. Ca 2+, HCO 3, CO 3 3) The free ion activity coefficients for the complexes e. g. Ca. CO 3, Ca. HCO 3 Then: % Free = [Ca 2+] / Ca. T = 1 / {1 + Ca 2+ [CO 3] CO 3 / KCa. CO 3 + Ca 2+ [HCO 3 ] HCO 3 / KCa. HCO 3+ + Ca 2+ [SO 4] SO 4 / KCa. SO 4 }

Example: Speciation of Major Ion seawater first by Garrels and Thompson (1962) American Journal of Science, 260, p. 57 The speciation of major ion seawater consisted of 4 cations (Na+, K+, Ca 2+, Mg 2+) and 4 anions (Cl-, HCO 3 -, CO 3 2 -, SO 42 -). Solve simultaneously This system has 24 species that need concentrations (unknowns). 8 free ions 16 ion pairs (only 1: 1 complexes , e. g. Mg. SO 4º ) To solve for 24 unknowns we need 24 equations 8 mass balance equations (e. g. Ca. T = [Ca 2+] + [Ca. Cl+] + [Ca. CO 3º] + [Ca. HCO 3+] + [Ca. SO 4º]) 16 equilibrium constants, K

Assumptions 1. Cl- forms no complexes - this eliminates 5 unknowns by eliminating, the 4 Cl- ion pairs and making the Cl mass balance the trivial balance of (Cl. T = Cl-) 2. They assumed K+ forms no CO 32 - or HCO 3 - complexes – This eliminates 2 more unknowns. Now simplified to 17 unknowns. 3. They assumed that all single charged ions (both + and -) have the same free ion activity coefficient as HCO 3 - thus, HCO 3 = 0. 68 (see attached table) 4. They assumed that all neutral complexes had the value of H 2 CO 3 = 1. 13 5. For the first iteration they assumed that all the cations were 100% free. Is a good assumption because Cl- balances most of the cations and Cl- does not form complexes.

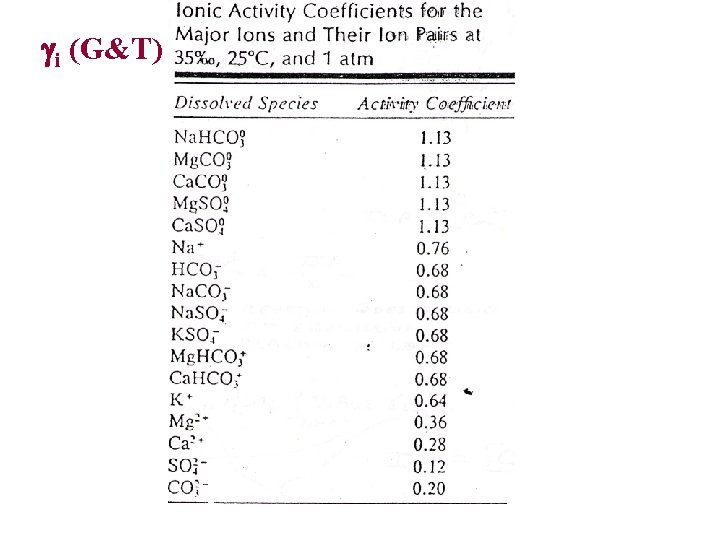
i (G&T)

Alkalinity = HCO 3 + 2 CO 3 = 0. 00238 + 2 (0. 000269) = 0. 002918 Eq

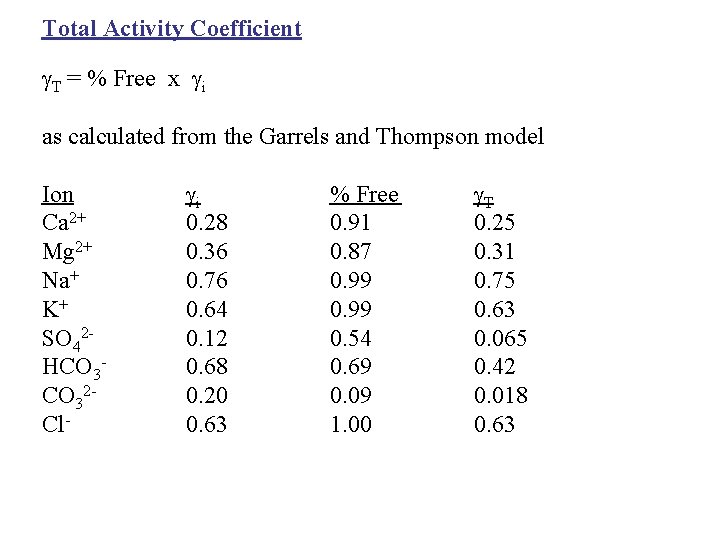
Total Activity Coefficient T = % Free x i as calculated from the Garrels and Thompson model Ion Ca 2+ Mg 2+ Na+ K+ SO 42 HCO 32 Cl- i 0. 28 0. 36 0. 76 0. 64 0. 12 0. 68 0. 20 0. 63 % Free 0. 91 0. 87 0. 99 0. 54 0. 69 0. 09 1. 00 T 0. 25 0. 31 0. 75 0. 63 0. 065 0. 42 0. 018 0. 63

Questions: How would solution composition change the solubility of gypsum (Ca. SO 4 • 2 H 2 O)? What would be the speciation of average river water? How would the speciation of hydrothermal vent solutions differ from seawater?