LECTURE 6 2 PRINCIPLES OF NUCLEAR FISSION REACTORS

LECTURE 6 2 PRINCIPLES OF NUCLEAR FISSION REACTORS SUMMARY OF UNDERLYING PHYSICS • Neutrons can induce fission in heavy nuclei • ~ 200 Me. V is released per fission • ~ 2. 5 neutrons per fission are released • s. F is large at certain energies 2. 1 CHAIN REACTIONS • If no absorption or loss of neutrons occurred then an initial neutron in a block of uranium can start a chain reaction • E. g. For simplicity assume 2 neutrons per fission Nuclear Energy Lecture 6 1 J N Jackson

• Define REPRODUCTION CONSTANT k (or MULTIPLICATION FACTOR) • k>1 ‘Super-critical’ – explosion (bomb) • k<1 ‘Sub-critical’ – reaction dies out • k=1 ‘Critical’ – stable chain reaction • Excess reactivity dk = k - 1 • k depends on many factors including the cross sections. Natural Uranium (Infinite system) • No chain reaction possible • As neutrons slow from 2 Me. V to 1 ke. V sc becomes dominant over sf Enriched Uranium (with 235 U) • Chain reaction possible • For all values of Tn, sf (235 U) > sc • Shows basis for FAST REACTORS in which mostly high energy neutrons cause fission 2 Nuclear Energy Lecture 6 J N Jackson

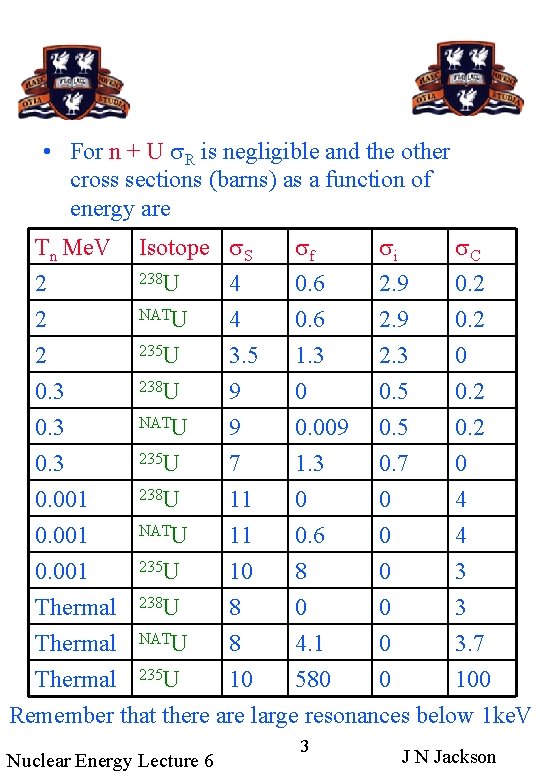
• For n + U s. R is negligible and the other cross sections (barns) as a function of energy are Tn Me. V 2 2 2 Isotope 238 U NATU 235 U s. S 4 4 3. 5 sf 0. 6 1. 3 si 2. 9 2. 3 s. C 0. 2 0 238 U 0. 3 9 0 0. 5 0. 2 NATU 0. 3 9 0. 009 0. 5 0. 2 235 U 0. 3 7 1. 3 0. 7 0 238 U 0. 001 11 0 0 4 NATU 0. 001 11 0. 6 0 4 235 U 0. 001 10 8 0 3 Thermal 238 U 8 0 0 3 Thermal NATU 8 4. 1 0 3. 7 Thermal 235 U 10 580 0 100 Remember that there are large resonances below 1 ke. V Nuclear Energy Lecture 6 3 J N Jackson

MODERATED NATURAL URANIUM • As Tn 0 there is increased probability of chain reactions in 235 U and NATU • Trick is to slow the neutrons to thermal energies without losing too many • Achieve this by having U fuel in rods of diameter d < l. FUEL (The mean free path in the fuel) • Neutrons escape from fuel rods into the MODERATOR where they slow down without significant absorption – Thus avoid capture resonances in 238 U • Neutrons slow to thermal energies and drift into fuel rods causing further fission • This is the basis of the THERMAL REACTOR Nuclear Energy Lecture 6 4 J N Jackson

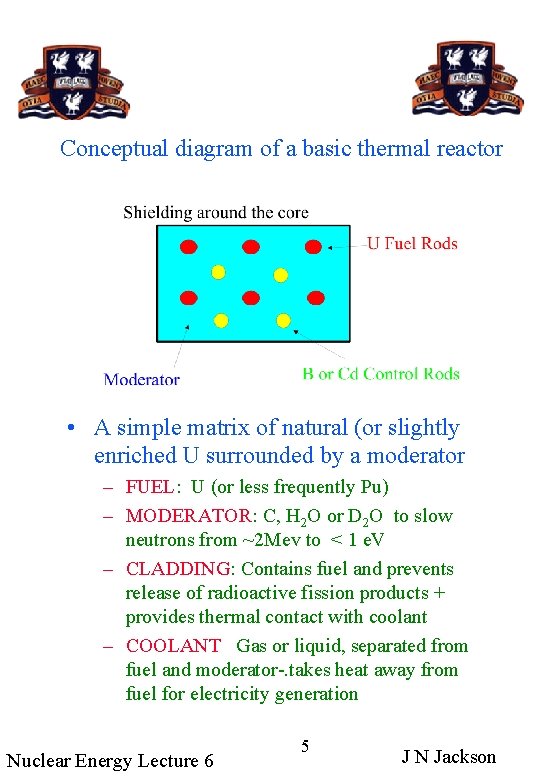
Conceptual diagram of a basic thermal reactor • A simple matrix of natural (or slightly enriched U surrounded by a moderator – FUEL: U (or less frequently Pu) – MODERATOR: C, H 2 O or D 2 O to slow neutrons from ~2 Mev to < 1 e. V – CLADDING: Contains fuel and prevents release of radioactive fission products + provides thermal contact with coolant – COOLANT Gas or liquid, separated from fuel and moderator-. takes heat away from fuel for electricity generation Nuclear Energy Lecture 6 5 J N Jackson

– CONTROL RODS Usually B (or Cd )with large s. C for thermal neutrons to maintain k=1 – SHIELD Usually steel to contain pressure and concrete to give radiation protection 2. 2 ROLE OF THE MODERATOR • The moderator slows neutrons by elastic scattering – E. g. General case : - • Let the masses of n and X be m and M respectively • In the Laboratory Frame X recoils in this process and so n loses energy in this frame • If we consider the process in the Centre of Mass System where n and X have equal and opposite momenta before and after scattering No loss of energy in this frame Nuclear Energy Lecture 6 6 J N Jackson

Consider the transformation to the centre of Mass system travelling with speed VC • In CMS mu 1 + Mu. X 1= 0 by definition • Also u 1 = u - VC and u. X 1 = - VC Substituting for u 1 and u. X 1 gives VC = u m / (m + M) and u 1 = u M / (m +M) • Now consider the final velocities of the neutron, v and v 1 in lab. and CMS, and v. X 1 the corresponding velocities for X. • In CMS mv 1 + Mv. X 1=0= mu 1 + Mu. X 1 |v 1 | = |u 1 | and |v. X 1 | = |u. X 1 | Nuclear Energy Lecture 6 7 J N Jackson

• The velocity v may be found from the following triangle of velocities using the cosine rule • Substituting for VC and v 1 we obtain • Let T 0 and T 1 represent the neutron K. E. before and after collision so T 0 = ½ m u 2 and T 1 = ½ m v 2 • If A is the mass number of X then M=A u and m= 1 u Nuclear Energy Lecture 6 8 J N Jackson

• The maximum energy loss occurs when cos(q) = -1 with T 1 a minimum – i. e. q =1800 (head-on collision), • Experiment shows that the angular distribution of the neutrons is isotropic in the C. M. S. • N. B. f is the azimuthal angle and the –ve sign occurs because T 1 decreases as q increases • Integrating over f gives : - Nuclear Energy Lecture 6 9 J N Jackson

• For rapid moderation we need A as small as possible – e. g. to reduce Tn from 2 Me. V to 0. 025 e. V takes ~ 20 collisions for hydrogen but ~ 100 for carbon • Practical considerations for choice of moderator are 1) small A, 2) large s. S, and 3) small s. A ( = s. C + s. R) Nuclear Energy Lecture 6 10 J N Jackson

CHOICES s. S (b) s. A (b) H 2 O 50 0. 66 D 2 O 11 0. 001 GRAPHITE 4. 7 0. 0045 • N. B. If H 2 O is used then U must be enriched with 235 U because the absorption s. A is large for H 2 O Nuclear Energy Lecture 6 11 J N Jackson