Lecture 6 2 Modularity Maximization DingZhu Du University

Lecture 6 -2 Modularity Maximization Ding-Zhu Du University of Texas at Dallas lidong. wu@utdallas. edu

Model-Based Detections • • • Connection-based detection Modularity maximization Influence-based detection Overlapping community detection Hierarchy community detection 2

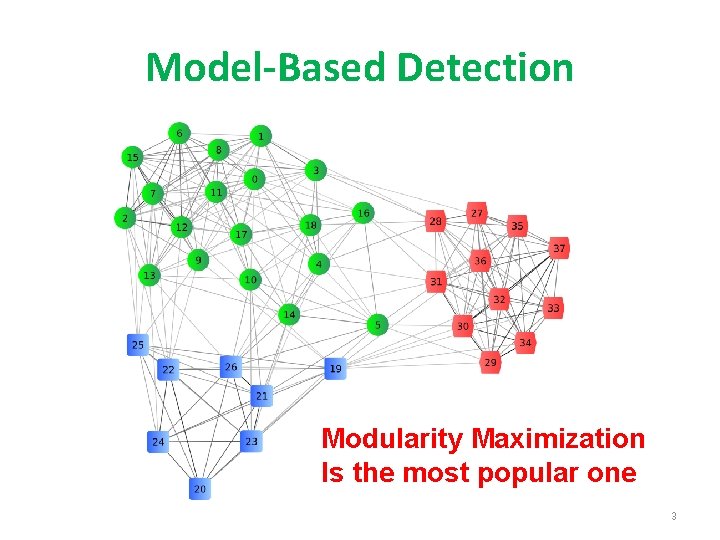
Model-Based Detection Modularity Maximization Is the most popular one 3

Outline v Modularity Function v Greedy v Spectral Method and MP v. Hybrid Method 4

Modularity Function (Newman 2006) 5

6

Modularity Function (Newman 2006) 7

Newman 2006 • M. E. J. Newman: Modularity and community structure in networks, Proceedings of the National Academy of Sciences, vol 103 no 23 (2006) pp. 8577 -8582. 8

Modularity Function 9

Modularity Function (Newman 2006) 10

Modularity Function (digraph) 11

Why call Modularity? • Module = community in some complex networks • The function describes the quality of modules. 12

Modularity Max is NP-hard • U. Brandes, D. Delling, M. Gaertler, R. Gorke, M. Hoefer, Z. Nikoloski, and D. Wagner: On modularity clustering, IEEE Transactions on Knowledge and Data Engineering (TKDE), vol 20, no 2 (2008) pp 172 -188 13

Outline v Modularity Function v Greedy v Spectral Method v. Hybrid Method 14

Increment 15

Greedy Algorithm 16

Outline v Modularity Function v Greedy v Spectral Method and MP v. Hybrid Method 17

Qualified Cut Community Partition 18

Quadratic Form 19

Spectral Method 20

Linear Program 21

Vector Program Semi-definite Program 22

Outline v Modularity Function v Greedy v Spectral Method and MP v. Hybrid Method 23

Resolution limit • Misidentification: some derived communities do not satisfy the weak community definition or even the most weak community definition • In other words, obtained communities may have sparser connection within them than between them. 24

Hybrid Detection: a Possible Research Direction

Max Q s. t. condition (1) • • • This may give an improvement. Is it possible to do? (1) can be written as linear constraints Q can be written as a quadratic function Thus, Max Q s. t. (1) can be formulated as a quadratic programming, which can be transformed into a semi-definite programming 26

Linear Constraints 27

Linear Constraints 28

Modularity Density function (Li et al. 2008) 29

Opt D s. t. condition (1) • • • This may give an improvement. Is it possible to do? (1) can be written as linear constraints Q can be written as a fractional function Thus, Max D s. t. (1) can be formulated as a Geometric Programming. 30

Outline v Community Structure v Connection-Based Detection v Influence-Based Detection v Remarks 31

Remark 1 How to evaluate the method for finding a community? 32

Clustering 33

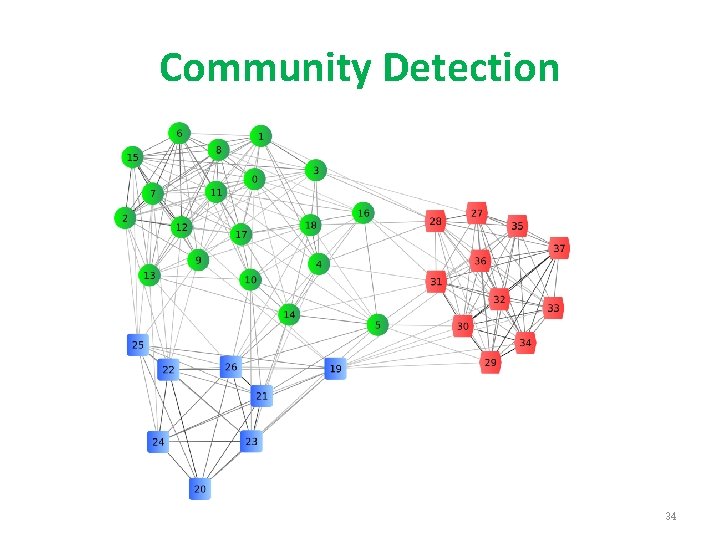
Community Detection 34

Remark 2 How to do hierarchy community detection? 35

Survey • Introductory review: Communities in networks by M. A. Porter, J. -P. Onnela, and P. J. Mucha, Notices of the American Mathematical Society 56, 1082 (2009) • Comprehensive review: Community detection in graphs by Santo Fortunato, Physics Reports 486, 75 (2010) 36

THANK YOU!