Lecture 5 Simple Circuits Series connection of resistors

Lecture 5 ØSimple Circuits. Ø Series connection of resistors. ØParallel connection of resistors. ØSeries and Parallel connection of resistors. ØSmall signal analysis. ØCircuits with capacitors and inductors. ØSeries connection of capacitors. ØParallel connection capacitors ØSeries connection of inductors. ØParallel connection inductors. 1

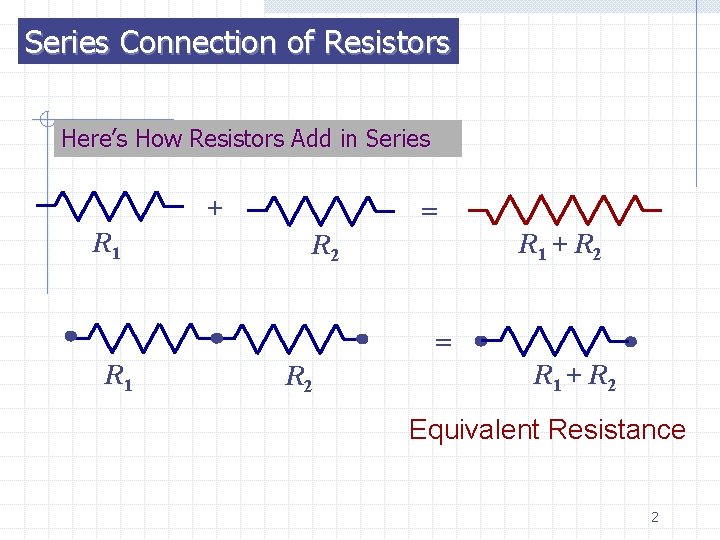
Series Connection of Resistors Here’s How Resistors Add in Series + R 1 = R 1 + R 2 = R 1 R 2 R 1 + R 2 Equivalent Resistance 2

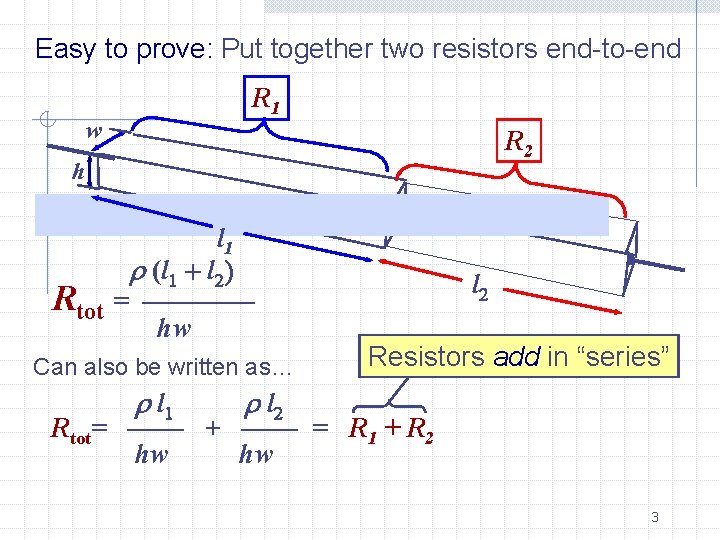
Easy to prove: Put together two resistors end-to-end R 1 w R 2 h l 1 (l 1 + l 2) Rtot = ———— hw Can also be written as… l 1 l 2 Resistors add in “series” l 2 Rtot= —— + —— = R 1 + R 2 hw hw 3

Example 1 Let us consider the circuit in Fig. 5. 1, where two nonlinear resistors R 1 and R 2 are connected at node B. Nodes A and C are connected to the rest of the circuit, which is designed by P. The one-port, consisting of resistor R 1 and R 2 , whose terminals are nodes A and C, is called the series connection of resistors R 1 and R 2. A R 1 B P R 2 C i 1 + v 1 - i 2 + v 2 - The two resistors R 1 and R 2 are specified by their characteristics, as shown in the vi plane in Fig. 1. 2. We wish to determine the characteristic of the series connection of R 1 and R 2 that is the characteristic of a resistor equivalent to the series connection. First KVL for the mesh ABCA requires that (5. 1) Next KCL for the nodes A, B, and C requires that Fig. 5. 1 The series connection of R 1 and R 2 4

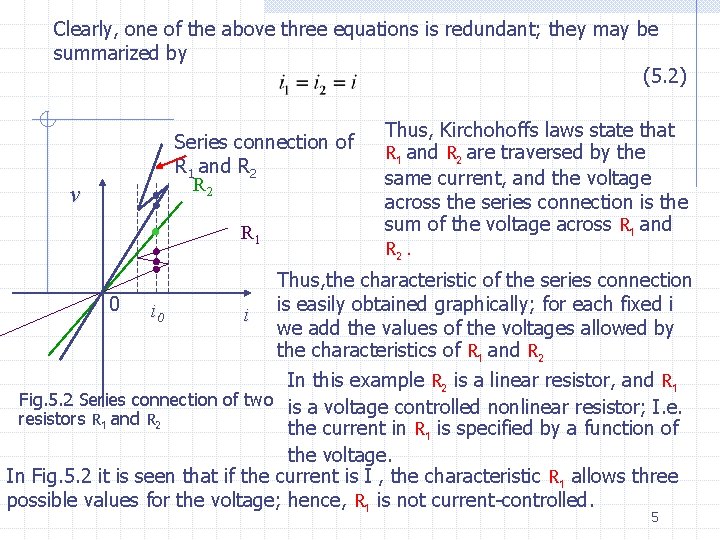
Clearly, one of the above three equations is redundant; they may be summarized by (5. 2) Series connection of R 1 and R 2 v R 1 0 i Thus, Kirchohoffs laws state that R 1 and R 2 are traversed by the same current, and the voltage across the series connection is the sum of the voltage across R 1 and R 2. Thus, the characteristic of the series connection is easily obtained graphically; for each fixed i we add the values of the voltages allowed by the characteristics of R 1 and R 2 In this example R 2 is a linear resistor, and R 1 Fig. 5. 2 Series connection of two is a voltage controlled nonlinear resistor; I. e. resistors R 1 and R 2 the current in R 1 is specified by a function of the voltage. In Fig. 5. 2 it is seen that if the current is I , the characteristic R 1 allows three possible values for the voltage; hence, R 1 is not current-controlled. 5

Analytically we can determine the characteristic of the resistor that is equivalent to the series connection of two resistors R 1 and R 2 only if both are current-controlled. Current controlled resistors R 1 and R 2 have that may be described by equations of the form (5. 3) where the reference directions are shown in Fig. 1. 1. In view of Eqs (5. 1) and (5. 2) the series connection has a characteristic given by (5. 4) Therefore we conclude that the two-terminal circuit as characterized by the voltage relation Eq. (5. 4) is another resistor specified by (5. 5 a) where (5. 5 b) 6

Equations (5. 5 a) and (5. 5 b) show that the series connection of the two current controlled resistors is equivalent to a current-controlled resistor R, and its characteritic is described by the function f( ) defined in (5. 5 b) (see fig. 5. 3). Using analogous reasoning, we Series connection of can state that the series R 1 and R 2 connection of m current R 2 controlled resistors with v characteristic described by R 1 vk=fk(ik), k=1, 2, …, m is equivalent to a single current controlled resistor whose characteristic is 0 described by v=f(i), where i 0 i Fig. 5. 3 Series connection of two current controlled resistors If, in particular, all resistors are linear; that is vk=fk(ik), k=1, 2, …, m the equivalent resistor is also linear, and v=Ri, Ri where (5. 6) 7

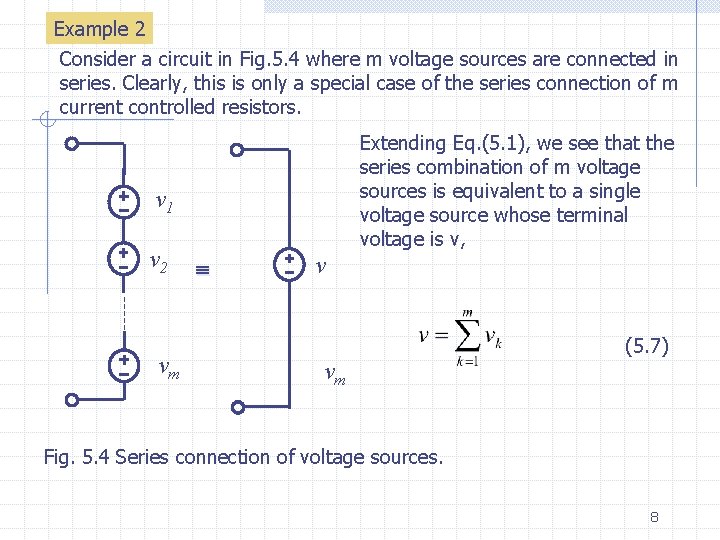
Example 2 Consider a circuit in Fig. 5. 4 where m voltage sources are connected in series. Clearly, this is only a special case of the series connection of m current controlled resistors. Extending Eq. (5. 1), we see that the series combination of m voltage sources is equivalent to a single voltage source whose terminal voltage is v, v 1 v 2 vm v vm (5. 7) Fig. 5. 4 Series connection of voltage sources. 8

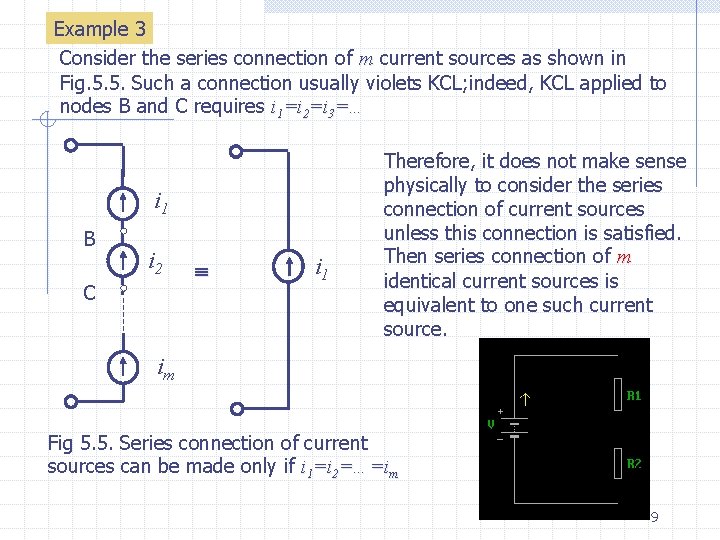
Example 3 Consider the series connection of m current sources as shown in Fig. 5. 5. Such a connection usually violets KCL; indeed, KCL applied to nodes B and C requires i 1=i 2=i 3=… i 1 B i 2 C i 1 Therefore, it does not make sense physically to consider the series connection of current sources unless this connection is satisfied. Then series connection of m identical current sources is equivalent to one such current source. im Fig 5. 5. Series connection of current sources can be made only if i 1=i 2=…=im 9

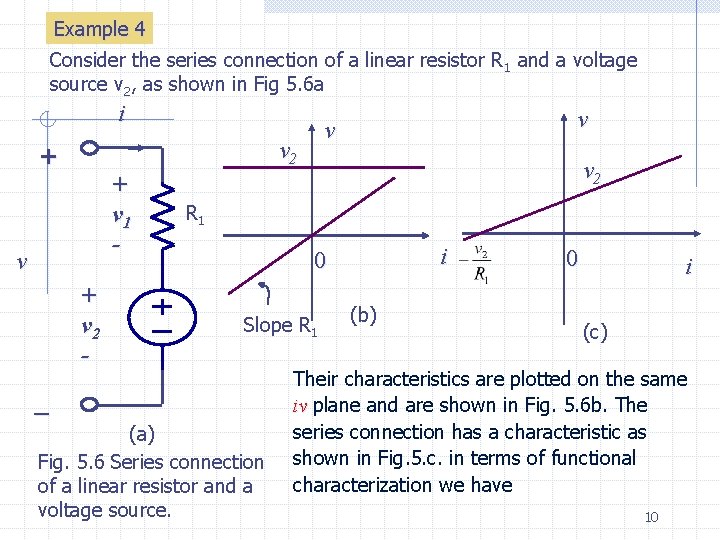
Example 4 Consider the series connection of a linear resistor R 1 and a voltage source v 2, as shown in Fig 5. 6 a i v 2 + + v 1 - v + v 2 - v v v 2 R 1 i 0 Slope R 1 _ (a) Fig. 5. 6 Series connection of a linear resistor and a voltage source. (b) 0 i (c) Their characteristics are plotted on the same iv plane and are shown in Fig. 5. 6 b. The series connection has a characteristic as shown in Fig. 5. c. in terms of functional characterization we have 10

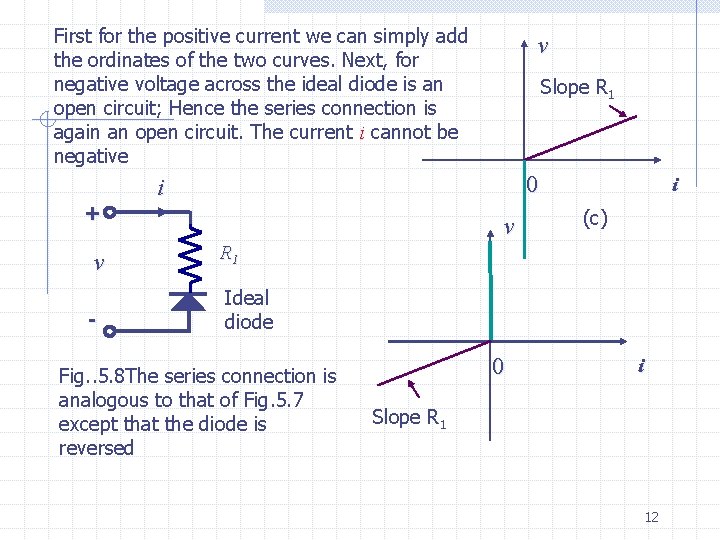
(5. 8) Sine R 1 is a known constant and v 2 known, Eq. (5. 8) relates all possible values of v and i. It is equation of a straight line as shown in Fig. 5. 6 c. Example 5 Consider the circuit of Fig. 5. 7 a where a linear resistor is connected to an ideal diode. Their characteristics are plotted on the same graph and are shown in Fig. 5. 7 b. The series connection has a characteristic as shown Fig. 5. 7 c. The series connection has a characteristic as shown in Fig. 5. 7 c it is obtained by reasoning as follows. v + v - v i Slope R 1 Ideal diode 0 Ideal diode (a) (b) Fig. 5. 7 Series connection of an ideal diode and a linear resistor 11 i

First for the positive current we can simply add the ordinates of the two curves. Next, for negative voltage across the ideal diode is an open circuit; Hence the series connection is again an open circuit. The current i cannot be negative + v Slope R 1 0 i v v R 1 - Ideal diode Fig. . 5. 8 The series connection is analogous to that of Fig. 5. 7 except that the diode is reversed 0 i (c) i Slope R 1 12

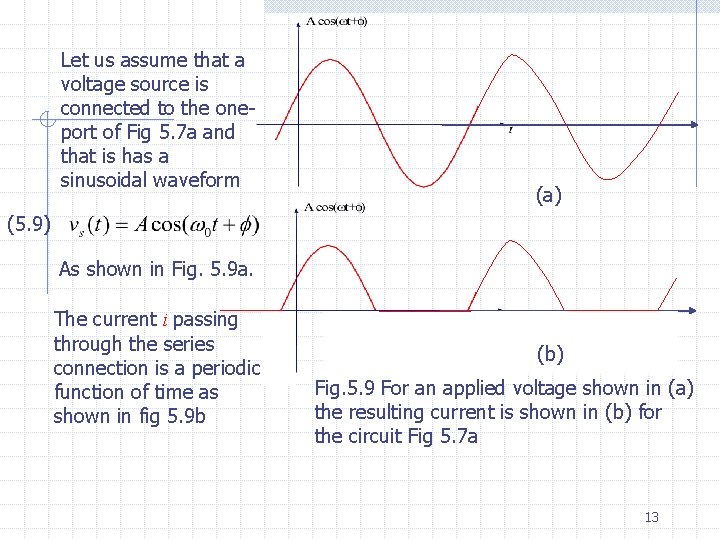
Let us assume that a voltage source is connected to the oneport of Fig 5. 7 a and that is has a sinusoidal waveform (a) (5. 9) As shown in Fig. 5. 9 a. The current i passing through the series connection is a periodic function of time as shown in fig 5. 9 b (b) Fig. 5. 9 For an applied voltage shown in (a) the resulting current is shown in (b) for the circuit Fig 5. 7 a 13

Observe that the applied voltage v( ) is a periodic function of time with zero average value. The current i( ) is also a periodic function of time with the same period, but it is always nonnegative. By use of filters it is possible to make this current almost constant; hence a sinusoidal signal can be converted into a dc signal. Summary For the series connection of elements, KCL forces the currents in all elements (branches) to be the same, and KVL requires that the voltage across the series connection be the sum of the voltages of all the brunches. Thus, if all the nonlinear resistors are current controlled, the equivalent resistor of the series connection has a characteristic v=f(i) which is obtained by adding the individual functions fk( ) which characterize the individual current-controlled resistors. For linear resistors the sum of individual resistance gives the resistance of the equivalent resistor, i. e. , for m linear resistors in series. 14

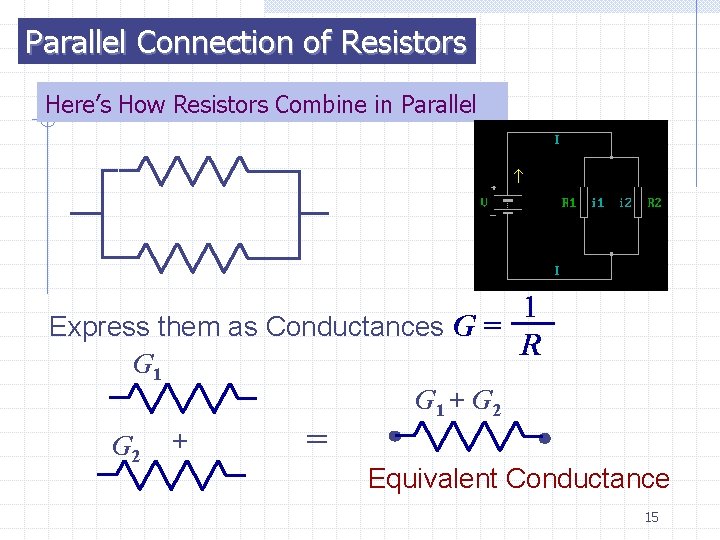
Parallel Connection of Resistors Here’s How Resistors Combine in Parallel 1 Express them as Conductances G = R G 1 G 2 + = G 1 + G 2 Equivalent Conductance 15

Parallel Resistance Formula G 1 + G 2 = 1 1 R 1 + R 2 1 Req = = 1 = R + R 1 1 2 G 1 + G 2 + R 1 R 2 Shorthand Notation: R 1 || R 2 16

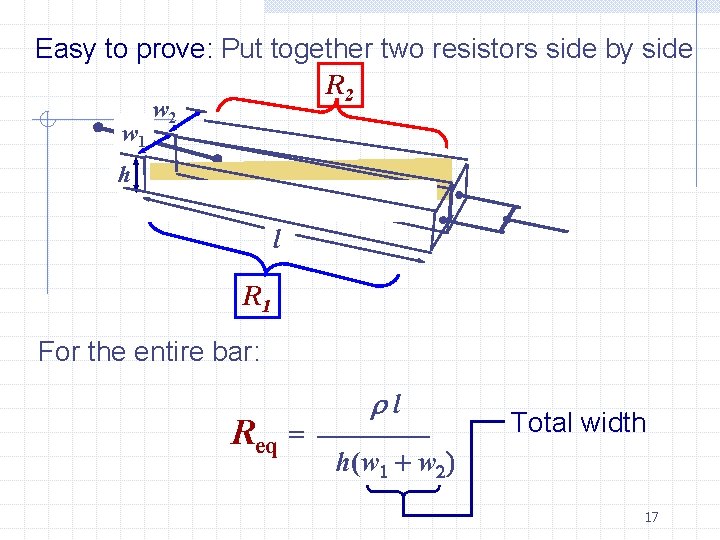
Easy to prove: Put together two resistors side by side R 2 w 1 w 2 h l R 1 For the entire bar: Req = l ———— h(w 1 + w 2) Total width 17

Req = l ———— h(w 1 + w 2) Multiply num. and den. by l (h w 1)(h w 2) Equation becomes… ( l) [( l)/ (h w 1)(h w 2)] Req= ————— h(w 1 + w 2) [( l)/ (h w 1)(h w 2)] Req = Resistors combine in “parallel” [( l)/ (h w 1)] [( l)/ (h w 2)] R 1 R 2 = R + R [ l/h w 1] + [ l/ h w 2] 1 2 18

Three or More Resistors in Parallel R 1 R 2 R 3 Rn For n resistors: – 1 1 1 Req = + + R 1 R 2 R 3 +. . . + Rn 19

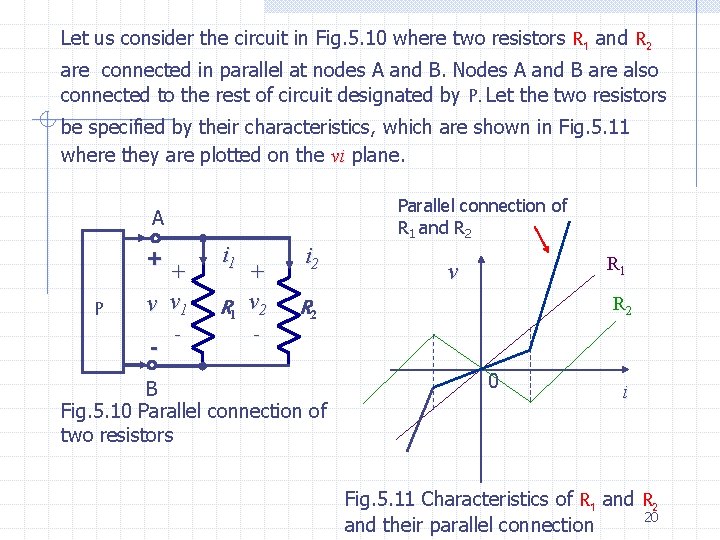
Let us consider the circuit in Fig. 5. 10 where two resistors R 1 and R 2 are connected in parallel at nodes A and B. Nodes A and B are also connected to the rest of circuit designated by P. Let the two resistors be specified by their characteristics, which are shown in Fig. 5. 11 where they are plotted on the vi plane. Parallel connection of R 1 and R 2 A + P + v v 1 - - i 1 + R 1 v 2 i 2 R 1 v R 2 - B Fig. 5. 10 Parallel connection of two resistors 0 i Fig. 5. 11 Characteristics of R 1 and R 2 20 and their parallel connection

Let us find the characteristic of the parallel connection of R 1 and R 2. Thus, Kirchhhofç laws imply that R 1 and R 2 have the same branch voltage, and the current through the parallel connection is the sum of the currents through each resistor. The characteristic of the parallel connection is thus obtained by adding, for each fixed v, the values of the current allowed by the characteristic of R 1 and R 2. The characteristic obtained in Fig. 5. 11 is that of the resistor equivalent to the parallel connection. Analytically, if R 1 and R 2 are voltage controlled, their characteristics may be described by equation of the form (5. 10) and in view of Kirchoff’s laws, the parallel connection has a characteristic described by (5. 11) In other words the parallel connection is described by the function g( ), defined by 21

(5. 12 a) where (5. 12 b) Extending this result to the general case, we can state that the parallel connection of m voltage controlled resistors with characteristic described by ik=gk(vk), k=1, 2, …, m is equivalent to a single voltagecontrolled resistor whose characteristic i=g(v), where If, in particular, all resistors are linear, that is the equivalent resistor is also linear, and , where (5. 13) G is the conductance of the equivalent resistor. 22

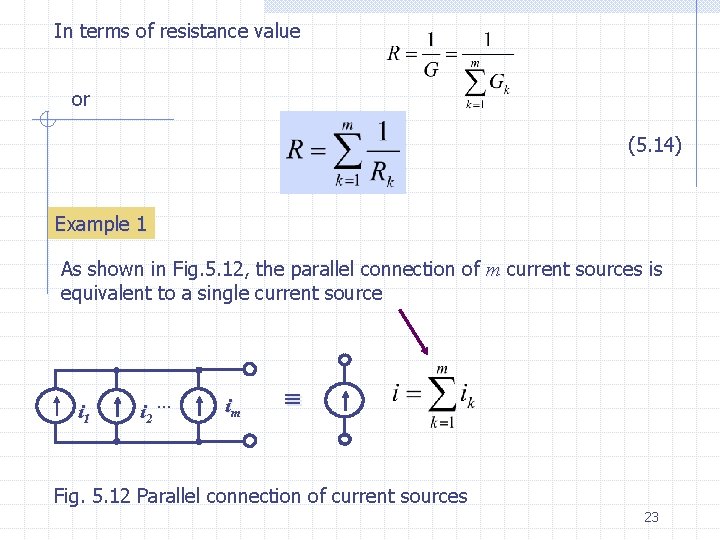
In terms of resistance value or (5. 14) Example 1 As shown in Fig. 5. 12, the parallel connection of m current sources is equivalent to a single current source i 1 i 2 im Fig. 5. 12 Parallel connection of current sources 23

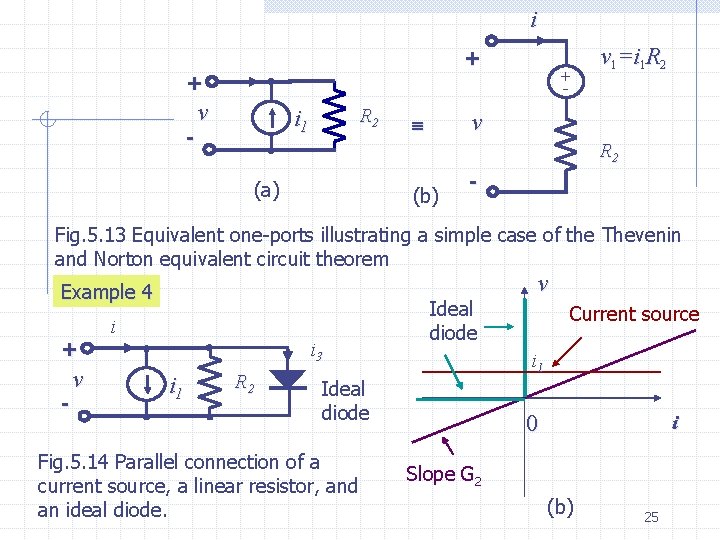
Example 2 The parallel connection of voltage sources violates KVL with exception of the trivial case where all voltage sources are equal. Example 3 The parallel connection of a current sources i 1 and linear resistor with resistance R 2 as shown in Fig. 5. 13 a can be represented by the equivalent resistor that is characterized by (5. 15) Eq. (2. 7) can be written as (5. 16) The alternative equivalent circuit can be drawn by interpreting the voltage v as the sum of two terms, a voltage source v 1=i 1 R 2 and a linear resistor R 2 as shown in Fig. 5. 13 b 24

i + + - v R 2 i 1 + - v 1=i 1 R 2 v R 2 (a) (b) - Fig. 5. 13 Equivalent one-ports illustrating a simple case of the Thevenin and Norton equivalent circuit theorem Example 4 + - v i i 3 i 1 R 2 Ideal diode Current source i 1 Ideal diode Fig. 5. 14 Parallel connection of a current source, a linear resistor, and an ideal diode. v 0 i Slope G 2 (b) 25

The parallel connection of a current source, a linear resistor, and an ideal diode is shown in Fig. 5. 14. a. Their characteristics re shown in Fig. 5. 14 b. The equivalent resistor has the characteristic shown in Fig 5. 14 c. For v negative the characteristic of the equivalent resistor is v obtained by the addition of thee curves. For i 3 positive the ideal diode is a short i 1 circuit; thus the voltage v across it is always zero. Summary Slope G 2 0 i (c) For the parallel connection of elements, KVL requires that all the voltages across the elements be the same, and KCL requires that the currents through the parallel connection be the sum of the currents in all the brunches. For nonlinear voltage-controlled resistors, the equivalent resistor of the parallel connection has a characteristic i=g(v) which is obtained by adding the individual functions gk( ) which characterize each individual voltage-controlled resistor. For linear resistors the sum of individual conductances gives the conductance the equivalent resistor. 26

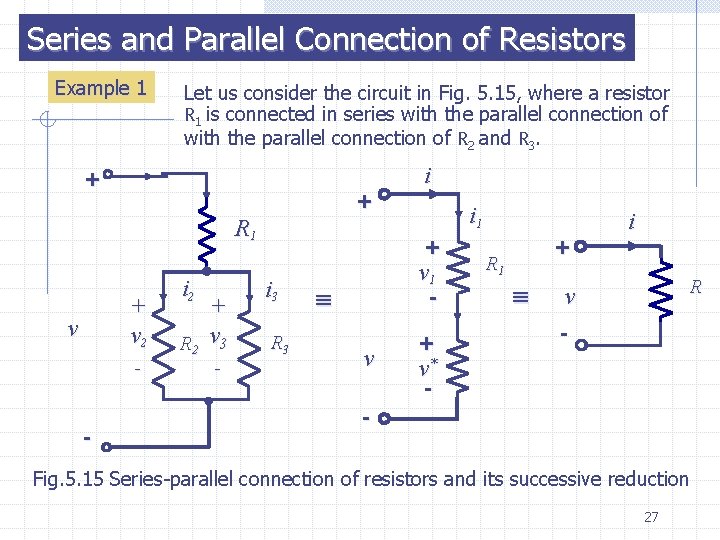
Series and Parallel Connection of Resistors Example 1 Let us consider the circuit in Fig. 5. 15, where a resistor R 1 is connected in series with the parallel connection of R 2 and R 3. + + R 1 + v 2 v - - i 2 + R 2 v 3 - i i 1 + i 3 R 3 v 1 - v + R 1 + i R v - v* - - Fig. 5. 15 Series-parallel connection of resistors and its successive reduction 27

If the characteristics of R 1, R 2 and R 3 are specified graphically, we need first to determine graphically the characteristic of R*, the resistor equivalent to the parallel connection of R 2 and R 3 , and second to determine graphically the characteristic of R, the resistor equivalent to the series connection of R 1 and R*. Let us assume that the characteristics of R 2 and R 3 are voltage controlled and specified by (5. 17) where g 2( ), and g 3( ), are single-valued functions. The parallel connection has an equivalent resistor R*, which is characterized by (5. 18) where i* and v* are the branch current and voltage of the resistor R* as shown in Fig. 5. 15. The parallel connection requires the voltages v 2 and v 3 to be equal to v*. The resulting current i* is the sum of i 2 and i 3. Thus, the characteristic of R*, is related to those of R 2 and R 3 by 28

(5. 19) Let g 2( ), and g 3( ), be specified as shown in Fig. 5. 16. Then g( ) is obtained by adding the two functions Voltage f Current g g-1 g 2 f 1 g 3 0 (a) Voltage 0 Current (b) Fig. 5. 16 Example 1: the series-parallel connection of resistors 29

The next step is to obtain the series connection of R 1 and R*. Let us assume that the characteristic of R 1 is current controlled an specified by (5. 20) where f 1( ) is a single-valued function as shown in Fig. 5. 16 b. The series connection of R 1 and R* has an equivalent resistor R as shown in Fig 5. 15. The characteristic of R as specified by (5. 21) Is to be determined. Obviously the series connection forces the currents i 1 and i* to be the same and equal to i. The voltage v is simply the sum ofv 1 and v*. However in order to add the two voltages we must first to be able to express v* in terms of i*. From (5. 18) we can write (5. 22) where g-1( ) is inverse of the function g 1( ) (See Fig. 5. 16 b). Thus the series connection of R 1 and R* is characterized by f( ) of (5. 21) where 30

Thus, the critical step in the derivation is the question of whether g-1( ) exists as a single –valued function. If the inverse does not exist, the reduction procedure fails; indeed, no equivalent representation exist in terms of single –valued functions. One simple criterion that guarantees the existence of such a representation is that all resistors have strictly monotonically increasing characteristics. In the case of linear resistors with positive resistance and monotonic increasing we can easily write the following: (5. 23) where R, R 1, R 2 and R 3 are respectively, the resistances R, R 1, R 2 and R 3 31

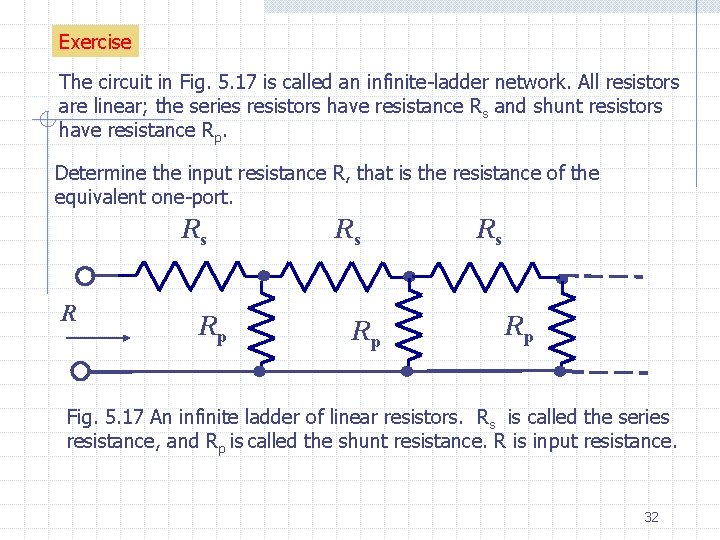
Exercise The circuit in Fig. 5. 17 is called an infinite-ladder network. All resistors are linear; the series resistors have resistance Rs and shunt resistors have resistance Rp. Determine the input resistance R, that is the resistance of the equivalent one-port. Rs R Rp Rs Rp Fig. 5. 17 An infinite ladder of linear resistors. Rs is called the series resistance, and Rp is called the shunt resistance. R is input resistance. 32

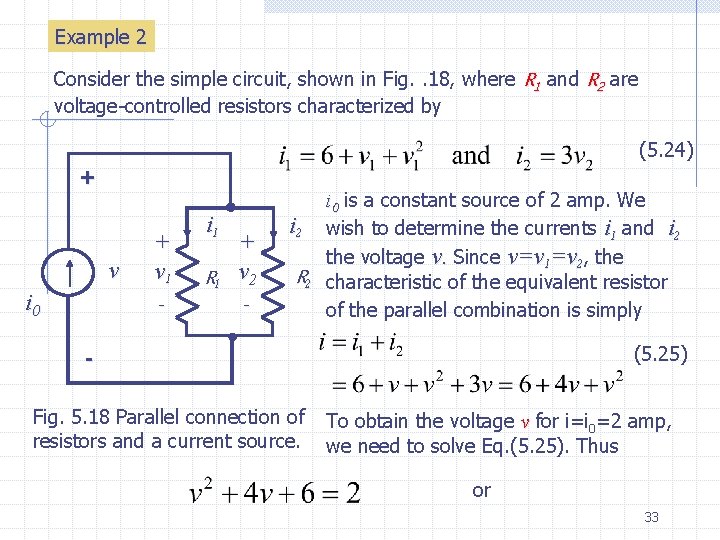
Example 2 Consider the simple circuit, shown in Fig. . 18, where R 1 and R 2 are voltage-controlled resistors characterized by (5. 24) + v i 0 + v 1 - i 1 + R 1 v 2 - i 0 is a constant source of 2 amp. We i 2 wish to determine the currents i 1 and i 2 the voltage v. Since v=v 1=v 2, the R 2 characteristic of the equivalent resistor of the parallel combination is simply (5. 25) Fig. 5. 18 Parallel connection of resistors and a current source. To obtain the voltage v for i=i 0=2 amp, we need to solve Eq. (5. 25). Thus or 33

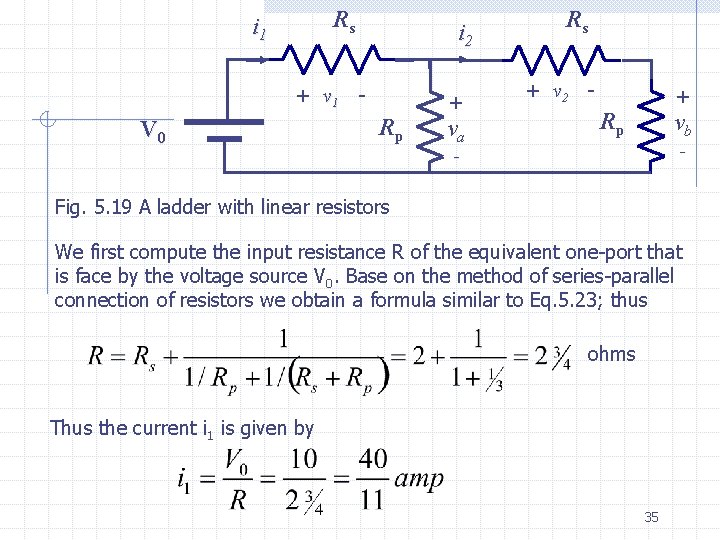
v=-2 volts Since v=v 1=v 2 , substituting (5. 26) in (5. 24) we obtain and i 1=8 amp (5. 26) i i 2=-6 amp Exercise Determine the power dissipated in each resistor and show that the sum of their power dissipations is equal to the power delivered by the current source Example 3 In the ladder of Fig. 5. 19, where all resistors are linear and timeinvariant, there are four resistors shown. A voltage source of V 0=10 volts is applied. Let Rs=2 ohm and Rp=1 ohm. Determine the voltage va and vb. 34

Rs i 1 i 2 + v 1 - V 0 + Rp va Rs + v 2 - + Rp vb - - Fig. 5. 19 A ladder with linear resistors We first compute the input resistance R of the equivalent one-port that is face by the voltage source V 0. Base on the method of series-parallel connection of resistors we obtain a formula similar to Eq. 5. 23; thus ohms Thus the current i 1 is given by 35

The branch voltage v 1 is given by Using KVL for the first mesh, we obtain Knowing va, we determine From Ohm’s law we have Thus by successive use of Kirchhoffs laws and Ohm’s law we can determine the voltages and currents of any series-parallel connection of linear resistors. 36

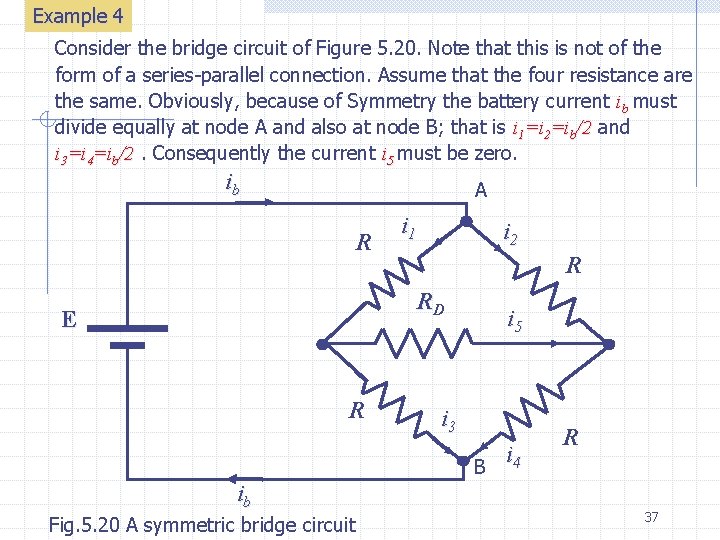
Example 4 Consider the bridge circuit of Figure 5. 20. Note that this is not of the form of a series-parallel connection. Assume that the four resistance are the same. Obviously, because of Symmetry the battery current ib must divide equally at node A and also at node B; that is i 1=i 2=ib/2 and i 3=i 4=ib/2. Consequently the current i 5 must be zero. ib A R i 1 i 2 R RD E R i 5 i 3 B ib Fig. 5. 20 A symmetric bridge circuit i 4 R 37

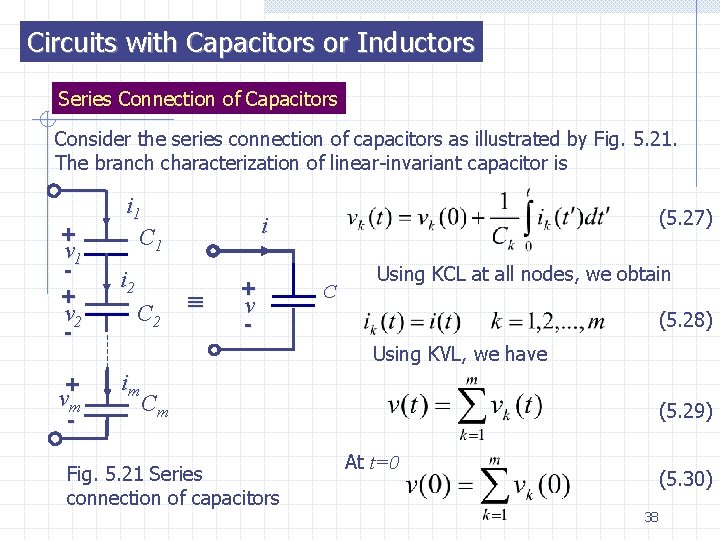
Circuits with Capacitors or Inductors Series Connection of Capacitors Consider the series connection of capacitors as illustrated by Fig. 5. 21. The branch characterization of linear-invariant capacitor is + v 1 + v 2 - + vm - i 1 C 1 i 2 C 2 (5. 27) i + v C Using KCL at all nodes, we obtain (5. 28) - Using KVL, we have im Cm Fig. 5. 21 Series connection of capacitors (5. 29) At t=0 (5. 30) 38

Combining Eqs. (5. 27) to (5. 30), we obtain (5. 31) Therefore the equivalent capacitor is given by (5. 32) The series connection of m linear time-invariant capacitors, each with value Ck and initial voltage vk(0), is equivalent to a single linear timeinvariant capacitor with value C, which is given by Eq. (5. 32) and initial voltage (5. 33) 39

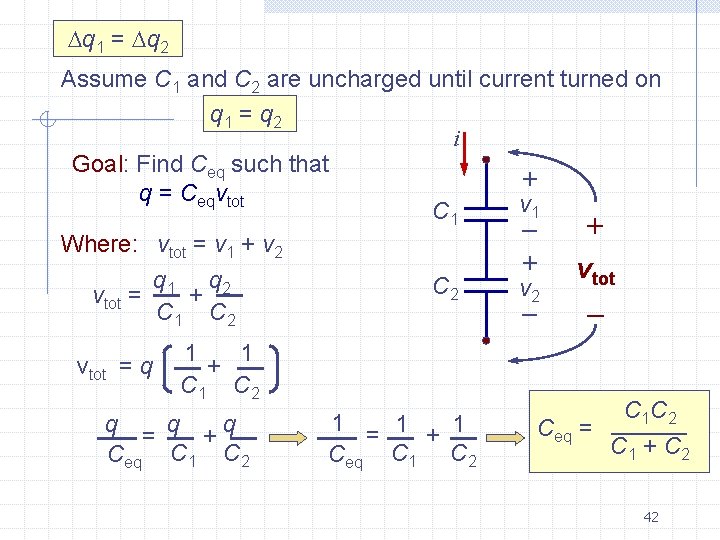
Connecting Capacitors in Series i What is the Equivalent Capacitance? + Can find using…. C 1 v 1 C 2 v 2 • Circuit theory • Physical argument – + – Here’s the result: Ceq = C 1 C 2 C 1 + C 2 Let’s show why… 40

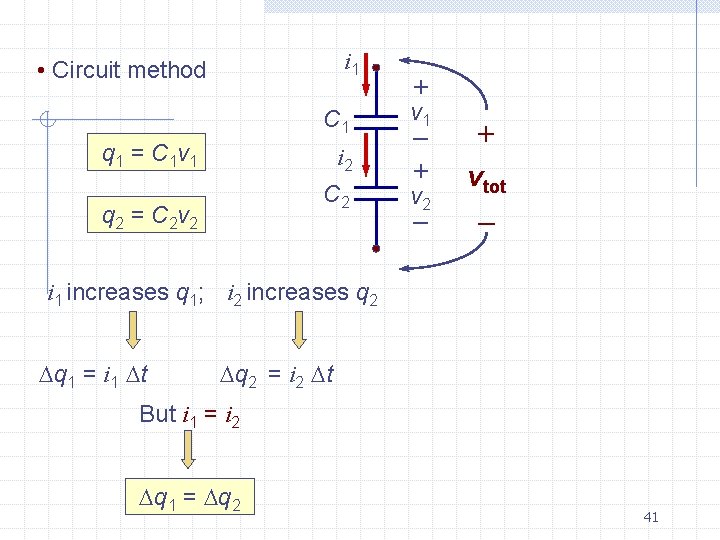
i 1 • Circuit method C 1 q 1 = C 1 v 1 i 2 C 2 q 2 = C 2 v 2 + v 1 + – + vtot – – v 2 i 1 increases q 1; i 2 increases q 2 q 1 = i 1 t q 2 = i 2 t But i 1 = i 2 q 1 = q 2 41

q 1 = q 2 Assume C 1 and C 2 are uncharged until current turned on q 1 = q 2 i Goal: Find Ceq such that + q = Ceqvtot v 1 C 1 + – Where: vtot = v 1 + v 2 q 1 q 2 vtot = + C 1 C 2 vtot = q C 2 1 1 + C 1 C 2 q q q = + Ceq C 1 C 2 1 = 1 + 1 Ceq C 1 C 2 + vtot – – v 2 C 1 C 2 Ceq = C 1 + C 2 42

Parallel Connection of Capacitors For the parallel connection of m capacitors we must assume that all capacitors have the same initial voltages, for otherwise KVL is violated at t=0 It is easy to show that for the parallel connection of m linear time invariant capacitors with the same voltage vk(0), the equivalent capacitor is equal to (5. 34) and i See Fig. 5. 22. v 1 + - C 1 v 2 (5. 35) + - C 2 • • • vm + + - Cm v C - Fig. 5. 22 Parallel connection of linear capacitors 43

Example Let us consider the parallel connection of two linear time invariant capacitors with different voltages. In Fig. 5. 23, capacitor 1 has capacitance C 1 and voltage V 1, and capacitor 2 has capacitance C 2 and voltage V 2. At t=0, t=0 the switch is closed so that the two capacitors are connected in parallel. What is a voltage across the parallel connection right after the closing of the switch? From (5. 34) the parallel connection has an equivalent capacitance (5. 36) At t=0 - the charge store in two capacitance is (5. 37) Ideal switch + C 1 V 1 - + V 2 - C 2 Since it is a fundamental principle of physics that electric charge is conserved at t=0+ (5. 38) Fig. 5. 23 The parallel connection of two capacitors with different voltages From (5. 36) through (5. 38) we can derive the new voltage across the parallel connection of the capacitors 44

Let the new voltage be V; then or (5. 39) Physically this phenomenon can be explained as follows: Assume V 1 is larger than V 2 and C 1 is equal C 2; thus, at time t=0 -, t=0 - the charge Q 1(0 -) is bigger than Q 2(0 -). At the time when the switch is closed, t=0 some charge is dumped from the first capacitor to the second instantaneously. This implies that an impulse of current flows from capacitor 1 to capacitor 2 at t=0 As a result, at t=0+, the voltages across the two capacitors are equalized to the intermediate value V required by the conservation of charge. 45

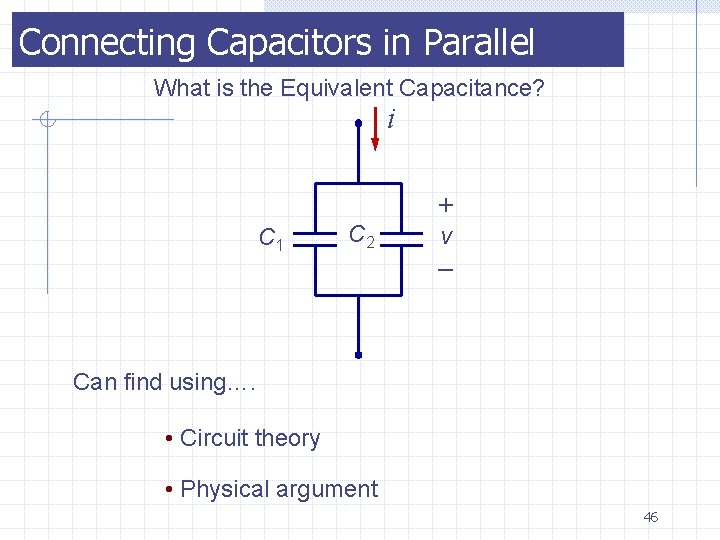
Connecting Capacitors in Parallel What is the Equivalent Capacitance? i C 1 C 2 + v – Can find using…. • Circuit theory • Physical argument 46

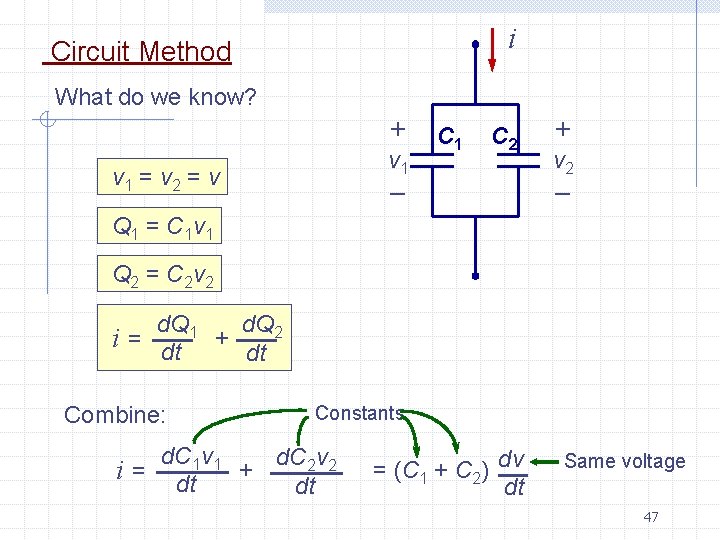
i Circuit Method What do we know? + v 1 = v 2 = v C 1 C 2 – + v 2 – Q 1 = C 1 v 1 Q 2 = C 2 v 2 d. Q 2 i = dt 1 + dt Combine: i= d. C 1 v 1 + dt Constants d. C 2 v 2 dt = (C 1 + C 2) dv dt Same voltage 47

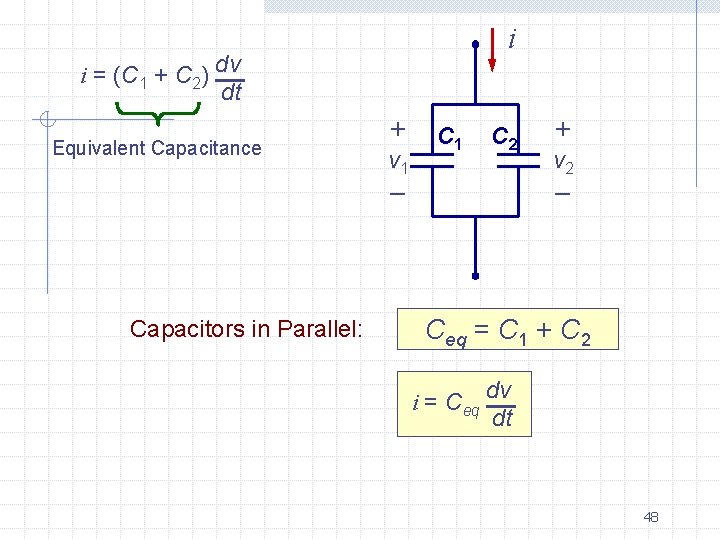
i i = (C 1 + C 2) dv dt Equivalent Capacitance + v 1 C 2 – Capacitors in Parallel: + v 2 – Ceq = C 1 + C 2 i = Ceq dv dt 48

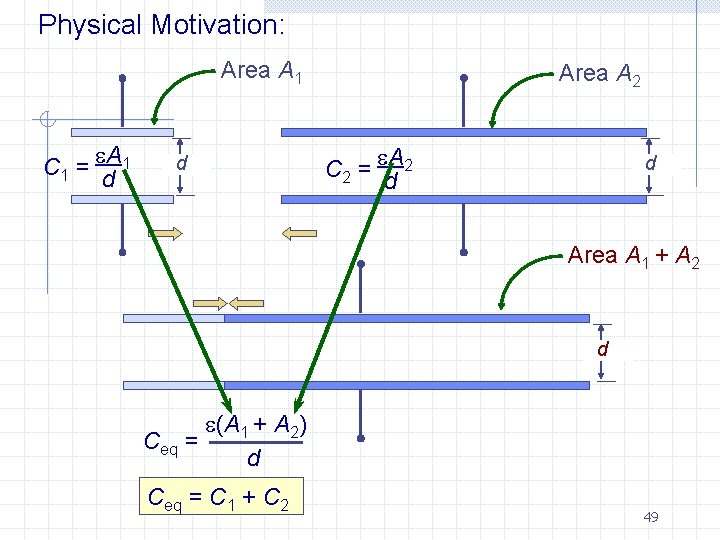
Physical Motivation: Area A 1 C 1 = A 1 d d Area A 2 C 2 = A 2 d d Area A 1 + A 2 d (A 1 + A 2) Ceq = d Ceq = C 1 + C 2 49

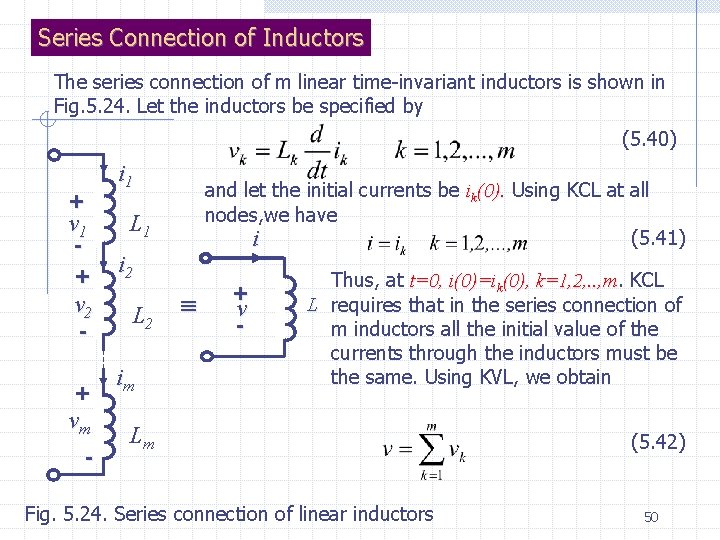
Series Connection of Inductors The series connection of m linear time-invariant inductors is shown in Fig. 5. 24. Let the inductors be specified by (5. 40) + v 1 + v 2 - + vm - i 1 and let the initial currents be ik(0). Using KCL at all nodes, we have (5. 41) i L 1 i 2 L 2 im + v - Thus, at t=0, i(0)=ik(0), k=1, 2, . . , m KCL L requires that in the series connection of m inductors all the initial value of the currents through the inductors must be the same. Using KVL, we obtain Lm Fig. 5. 24. Series connection of linear inductors (5. 42) 50

Combining Eqs. (5. 40) to (5. 42), we have (5. 43) Therefore, the equivalent inductance is given by (5. 44) The series connection of m linear time-invariant inductors each with Lk and initial current i(0), is equivalent to single inductor of inductance with the same initial current i(0). Parallel Connection of Inductors i 1 L 1 i 2 L 2 im • • • i + Lm v L 51

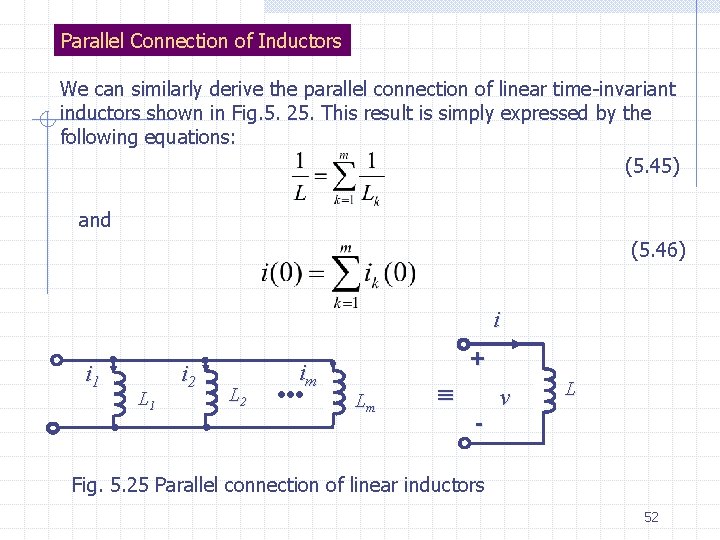
Parallel Connection of Inductors We can similarly derive the parallel connection of linear time-invariant inductors shown in Fig. 5. 25. This result is simply expressed by the following equations: (5. 45) and (5. 46) i i 1 L 1 i 2 L 2 im • • • + Lm v L - Fig. 5. 25 Parallel connection of linear inductors 52

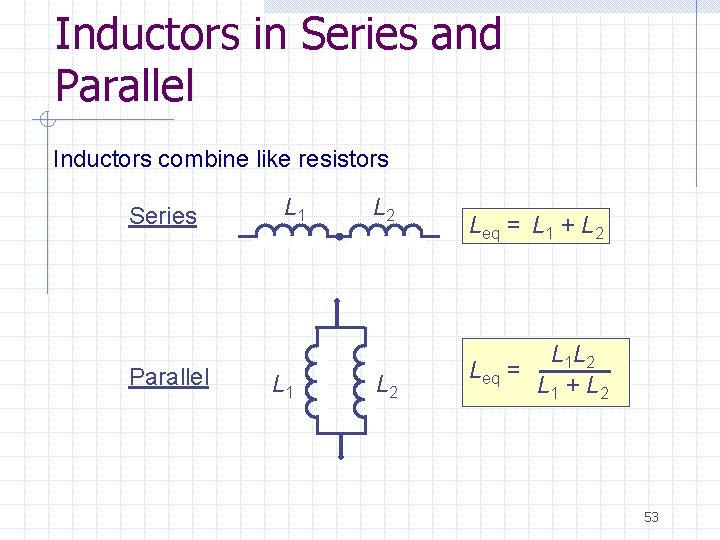
Inductors in Series and Parallel Inductors combine like resistors Series Parallel L 1 L 2 Leq = L 1 + L 2 L 1 L 2 Leq = L 1 + L 2 53

Summary In a series connection of elements, the current in all elements is the same. The voltage across the series connection is the sum of voltage across each individual element. In parallel connection of elements, the voltage across all elements is the same. The current through the parallel connection is the sum of the currents through each individual element. Type of elements Series connection of m elements Parallel connection of m elements Resistors R=resistance G=conductance C=capacitance S=elastance Inductors L=inductance 54