Lecture 5 Set Packing Problems Set Partitioning Problems

Lecture 5 Set Packing Problems Set Partitioning Problems 1

Outline èset packing problems èset partitioning problems 2

Set Packing Problems 3

Context èa set S = {1, 2…, m} èa collection of subsets of S, , such that each subset carry a value èproblem: to maximize the total value of subsets selected such that no element is selected more than once 4

Set Packing Problems è S = {1, 2, 3, 4, 5, 6} è = {{1, 2, 5}, {1, 3}, {2, 4}, {3, 6}, {2, 3, 6}} è examples è {1, 2, 5}, {3, 6}: a pack è {1, 3}, {2, 4}: a pack è {1, 2, 5}, {2, 3, 6}: not a pack è {2, 3, 6}: a pack è assumption: every subset of value = 1 5

Set Packing Problems èS = {1, 2, 3, 4, 5, 6} è = {{1, 2, 5}, {1, 3}, {2, 4}, {3, 6}, {2, 3, 6}} Property 9. 4: maximization with all constraints : element 1 : element 2 : element 3 Property 9. 5: all RHS coefficients = 1 : element 5 : element 6 set 5: set 3: set 4: set 2: i {0, 1} set 1: Property 9. 6: all matrix coefficients = 0 or 1 : element 4 6

Primal-Dual Pair è“An interesting observation is that the LP problem associated with a set packing problem with objective coefficients of 1 is the dual of the LP problem associated with a set covering problem with objective coefficients of 1. ” (pp 192 of [7]) 7

Primal-Dual Pair Primal (Dual) è Dual (Primal) special properties between the primal-dual pair è obj function of min obj function of max è unbounded primal infeasible dual è optimal primal optimal dual è è same objective function value è easy to deduce the optimal of one from the other possible to have infeasible primal and infeasible dual 8

Comments on Set Packing Problems set covering problem with objective coefficients = 1 set packing problem with objective coefficients = 1 dual of each other i 0 The two LPs are dual of each other, though the S and in one problem are different from those of the other problem. 9

Comments on Set Packing Problems èsimilar generalization as in set covering problems èweighted set packing problems: RHS positive integers > 1 ègeneralized set packing problems: matrix coefficients = 0 or 1 10

Matching Problem: A Special Type of Set Packing Problem èmatching: select the maximum numbers of arcs such that there is no overlapping of nodes involved 4 2 è(1, 2), (3, 6), (4, 5) 5 1 6 3 11
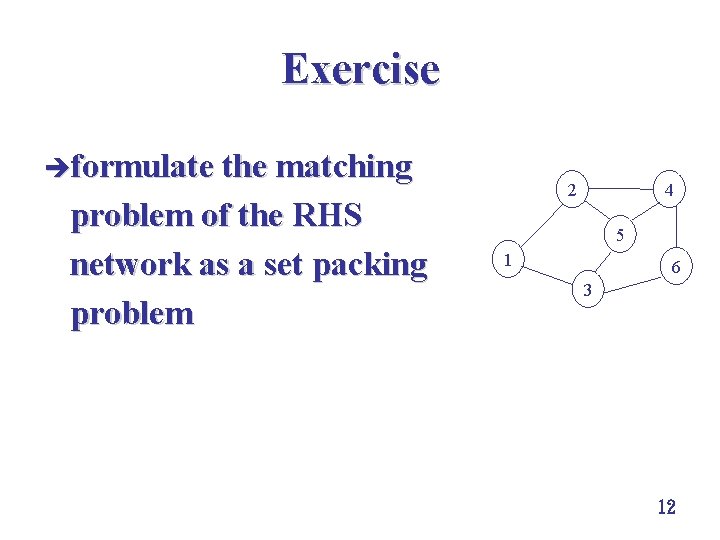
Exercise èformulate the matching problem of the RHS network as a set packing problem 4 2 5 1 6 3 12

Set Partitioning Problems 13

Set Partitioning Problems è to cover all the members of S by elements of without overlapping è S = {1, 2, 3, 4, 5} è = {{1, 2}, {1, 3, 5}, {2, 4, 5}, {3}, {1}, {4, 5}} è e. g. , {1, 2}, {3}, and {4, 5} form a partition 14

Set Partitioning Problems è S = {1, 2, 3, 4, 5} è = {{1, 2}, {1, 3, 5}, {2, 4, 5}, {3}, {1}, {4, 5}} either maximization or minimization is all right i {0, 1} 15

Equivalence Between Set Packing Problem and Set Partitioning Problem Set Packing Problem i {0, 1}, 1 to 11 16

Equivalence Between Set Packing Problem and Set Partitioning Problem èillustrate the transformation of the first equality constraint into an -constraint èintroduce a dummy variable to the first constraint Set Partitioning Problem max 1 + 2 + 3 + 4 + 5 + 6, i {0, 1} 17

Equivalence Between Set Packing Problem and Set Partitioning Problem max 1 + 2 + 3 + 4 + 5 + 6 M , Set Partitioning Problem max 1 + 2 + 3 + 4 + 5 + 6, i, {0, 1} i {0, 1} max (M+1) 1 + (M+1) 2 + 3 + 4 + (M+1) 5 + 6 M, max i, {0, 1} 18

Further Comments è set covering problems different from set packing problems and set partitioning problems è possible to transform a set packing problem into a set covering problem, but in general not the other way around è set covering problem more difficult to solve than the other two problems 19

A Simplified Air Crew Scheduling Problem 20

A Simplified Air Crew Scheduling Problem èsix flights every day, for cities A, B, and C, where A is the base 8 12 10 14 16 18 20 22 A B leg 1 leg 3 leg 5 leg 4 leg 2 leg 6 C 21

A Simplified Air Crew Scheduling Problem è pairings of legs for air crew: rules from regulation bodies and union è simplified rules in the example è at most eight hours flying time in a pairing è flying time in a pairing = sum of flying times in all legs of the pairing è at most two duties in a pairing è at least nine hours for overnight rest (OR) between duties 22

A Simplified Air Crew Scheduling Problem ècost of a pairing = time away from the base flying time of the pairing ècost of pairing 1 = 36 10 = 26 23

A Simplified Air Crew Scheduling Problem èsuppose only considering covering the 6 legs in a day èlet xj = 1 if the jth pairing is used, and xj = 0 otherwise 24

A Simplified Air Crew Scheduling Problem è a set partitioning problem è min 26 x 1 + 20 x 2 + 2 x 3 + 26 x 4 + 20 x 5 + 26 x 6, è s. t. è x 1 + x 2 è x 1 è è è + x 6 x 3 + x 4 + x 5 + x 6 x 2 + x 3 + x 4 + x 5 x 2 + x 5 = 1, x 5 + x 6 xi {0, 1} = 1, = 1, 25

A Simplified Air Crew Scheduling Problem è The dual of the partitioning problem è min 1 + 2 + 3 + 4 + 5 + 26 6, è s. t. è è è 1 + 2 1 + 4 + 5 3 + 4 + 5 + 6 2 + 3 + 6 ≤ 20 ≤ 26 26

To Construct a Simplified Air Crew Scheduling Problem 27
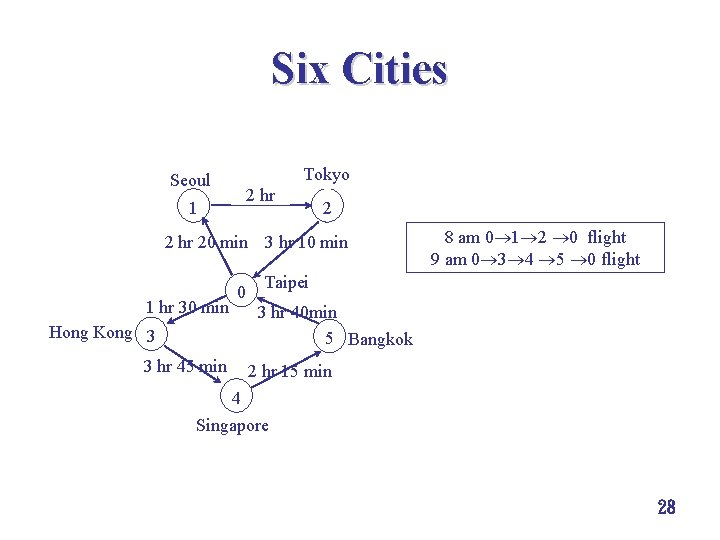
Six Cities Tokyo Seoul 2 hr 1 2 2 hr 20 min 3 hr 10 min 1 hr 30 min 0 8 am 0 1 2 0 flight 9 am 0 3 4 5 0 flight Taipei 3 hr 40 min 5 Bangkok Hong Kong 3 3 hr 45 min 2 hr 15 min 4 Singapore 28

Assumptions for Planes è It takes 90 minutes to load supply and passengers before departure (including unloading passengers for the previous flight leg, if applicable). è All flights are on exact time. è It takes 30 minutes for a plane to reach the terminal after arrival. è It takes 30 minutes to unload passengers and clean up a plane at the end of its service. 29
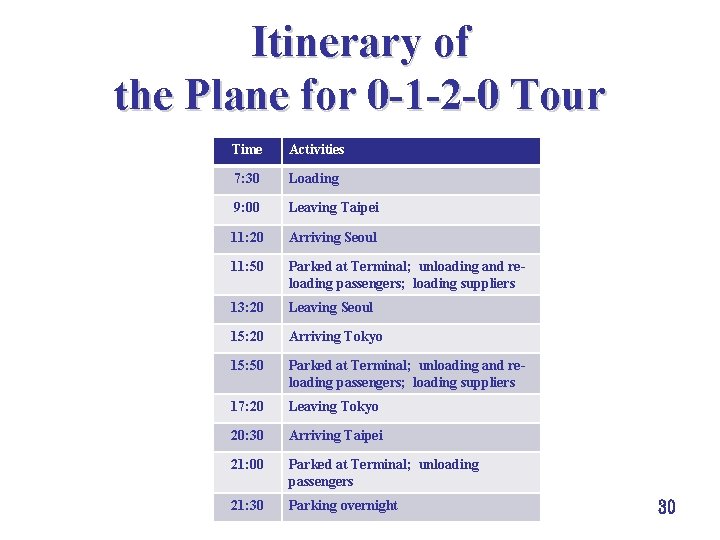
Itinerary of the Plane for 0 -1 -2 -0 Tour Time Activities 7: 30 Loading 9: 00 Leaving Taipei 11: 20 Arriving Seoul 11: 50 Parked at Terminal; unloading and reloading passengers; loading suppliers 13: 20 Leaving Seoul 15: 20 Arriving Tokyo 15: 50 Parked at Terminal; unloading and reloading passengers; loading suppliers 17: 20 Leaving Tokyo 20: 30 Arriving Taipei 21: 00 Parked at Terminal; unloading passengers 21: 30 Parking overnight 30

Exercise ègive the itinerary of the plane for 0 -3 -4 -5 -0 tour èbased on the itineraries of the planes for the 0 -1 -2 -0 and 0 -3 -4 -5 -0 tours, construct the requirements for air stewards and for pilots èput down all assumptions made 31
- Slides: 31