Lecture 5 OPERATIONS ON MATRICES MATH 20580 Introduction

Lecture 5 OPERATIONS ON MATRICES MATH 20580 Introduction to Linear Algebra & Differential Equations Spring 2021; Instructor: Dmitriy Voloshyn

Class Participation from 02/10 Are these two vectors linearly dependent (yes or no)? No Class Participation Question for this Friday!

Matrices A matrix is just a table of numbers. The size of the matrix is NUM OF ROWS × NUM OF COLS 3 columns For example, 2 rows the size is 2× 3 It’s a 2 by 3 matrix. A square matrix is the one with the same number of rows and cols. A square 2× 2 matrix. Its diagonal consists of 1 and 4. The identity matrix has 1 s on the diagonal and zeros everywhere else: the identity 3× 3 matrix A zero matrix – zeros everywhere: the zero 3× 3 matrix.

Two matrices are equal when they are of the same size and have the same entries. For example, We can multiply matrices by numbers: (compare to vectors) And we can add matrices entrywise: (compare to vectors) Similarly, can subtract matrices:

Matrix multiplication A step-by-step example: (compare to the dot product)

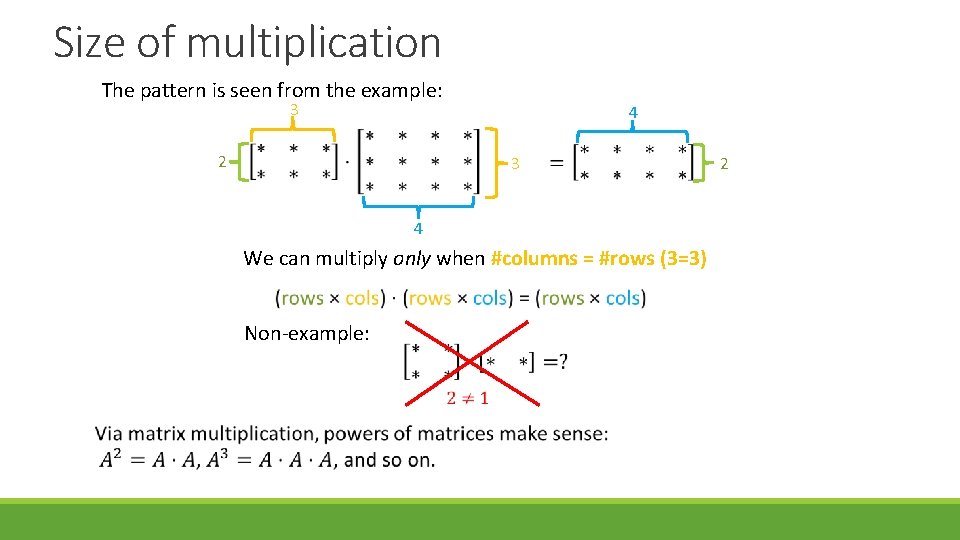
Size of multiplication The pattern is seen from the example: 3 2 4 3 4 We can multiply only when #columns = #rows (3=3) Non-example: 2

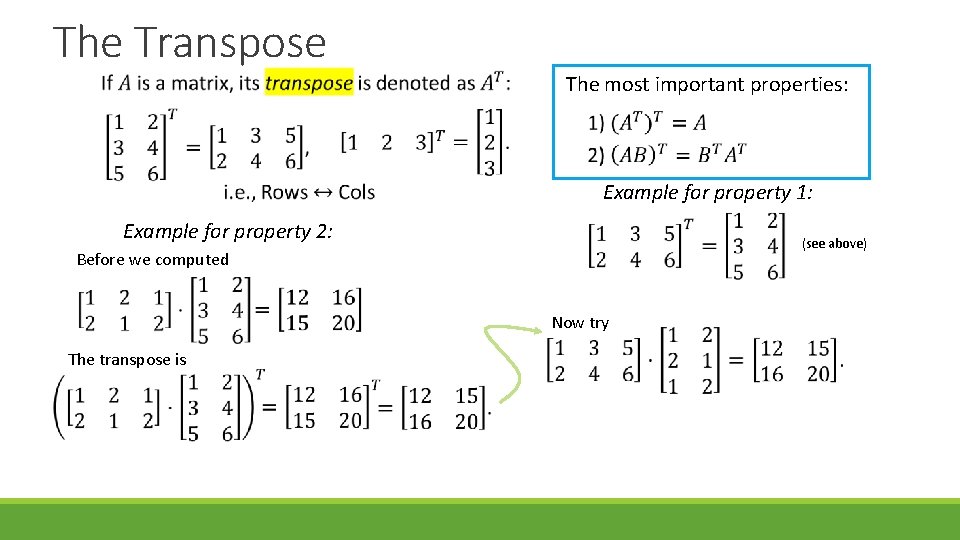
The Transpose The most important properties: Example for property 1: Example for property 2: (see above) Before we computed Now try The transpose is

Symmetric matrices A symmetric matrix Note: symmetric matrices must be square matrices! Some cases when a matrix is symmetric: Proof. Use properties 1) and 2):

Consider a system from Lecture 2: Its matrix of coefficients is (it’s almost the augmented matrix except no augmentation) Form vectors form variables and from the RHS:

The Inverse of a Matrix Something like Answer: sometimes yes.

The Formula for 2× 2 case Consider the most general 2× 2 matrix: Proof. Just multiply the two: Solution. Use the formula: