Lecture 5 Interference and diffraction of light II

Lecture 5: Interference and diffraction of light (II) Interference in Thin Films (Y&F 35. 4) o Thin films on a substrate undergo the phenomenon of multiple wave interference. o Examples are the bright bands of colour from a thin layer of oil floating on water, the patterns in soap bubbles, antireflective coatings in glasses. Thin film of oil on water n 1 n 2 n 3 t d n 1< n 2 < n 3 P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 1

Geometric description of thin film interference o Interference between bc and ef: • At b there is a reflection: change of phase = p (D r = l 2 /2) if n 1<n 2 • At d there is a reflection: change of phase = p (D r = l 2 /2) if n 2<n 3 So constructive interference when: bc + l 2 /2 - (bd + de +ef +l 2 /2) = ml 2 a n 1 f l 2 = wavelength in medium n 2 o If light perpendicular: bd + de = 2 t bc=ef c b e n 2 n 3 t d n 1< n 2 < n 3 Therefore: 2 t=ml 2 for constructive interference m=0, 1, 2, … 2 t=(m+1/2)l 2 for destructive interference m=0, 1, 2, . . . P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 2

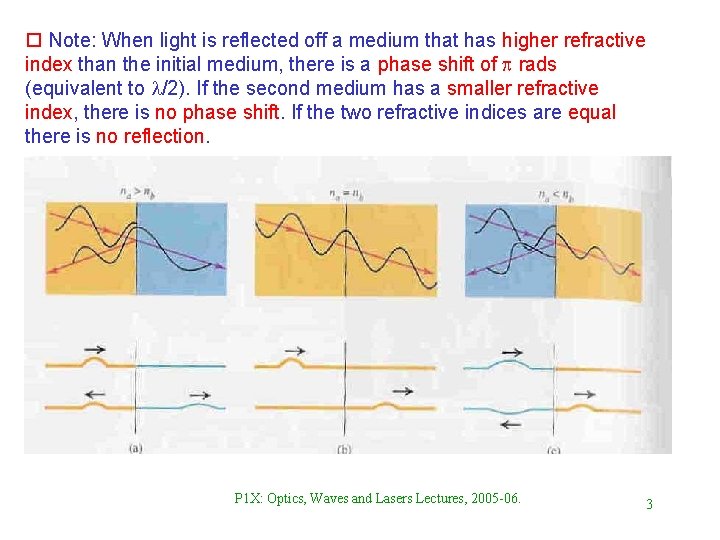
o Note: When light is reflected off a medium that has higher refractive index than the initial medium, there is a phase shift of p rads (equivalent to l/2). If the second medium has a smaller refractive index, there is no phase shift. If the two refractive indices are equal there is no reflection. P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 3

Examples of thin film interference o Non-reflective coatings: • We want to create a thin film on a substrate that is non-reflective, so we want destructive interference. • If we have a “quarter-wave” plate: t=l 2 / 4 then: Path difference = 2 t = l 2 /2 (destructive interference) v 1=c/n 1 so: fl 1 = c/n 1 l 2 = c/ (f n 2) = l 1 (n 1/n 2) v 2=c/n 2 so: fl 2 = c/n 2 If n 1 = 1 (air) then: l 2 = l 1/n 2 therefore: 2 t= l 2/2 = l 1/(2 n 2) o The optical path-length between two interfering waves is: 2 t n 2 = l 1/2 physical path-length P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 4

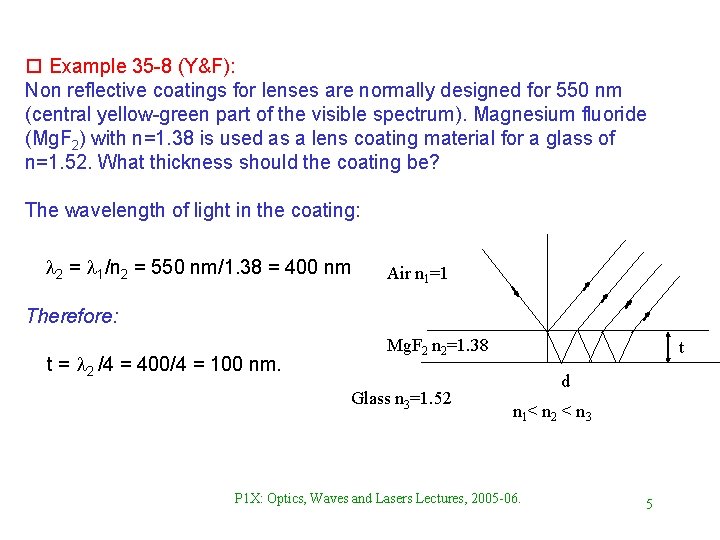
o Example 35 -8 (Y&F): Non reflective coatings for lenses are normally designed for 550 nm (central yellow-green part of the visible spectrum). Magnesium fluoride (Mg. F 2) with n=1. 38 is used as a lens coating material for a glass of n=1. 52. What thickness should the coating be? The wavelength of light in the coating: l 2 = l 1/n 2 = 550 nm/1. 38 = 400 nm Air n 1=1 Therefore: t = l 2 /4 = 400/4 = 100 nm. Mg. F 2 n 2=1. 38 Glass n 3=1. 52 t d n 1< n 2 < n 3 P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 5

o Interference in an air wedge between two glass plates: • Ray 1: reflected at A (no phase change) • Ray 2: travels path ABC (phase change of p at B) Difference is ABC = 2 t - l/2 (it q is small). 1 2 o Constructive interference: 2 t - l/2 = ml n 1 n 2 n 3 A q xm C t h o Destructive interference: 2 t + l/2 = (m+1/2)l B 2 t = (m+1/2)l 2 t =ml L o Distance xm from line of contact to mth dark fringe: Since 2 tm =ml and xm = tm(L/h) then: xm = (ml/2)(L/h) P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 6

o Newton’s rings: interference between a curved lens (radius R) and a flat glass plate inside a medium of refractive index n (e. g. n=1 for air and n= 1. 33 for water). Observation of concentric dark and light fringes with centre in the centre of the lens. P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 7

o Phase change of p (equivalent to l/2) at the bottom surface reflection: r 1 -r 2= 2 t therefore: Optical path length = n(r 1 -r 2) = 2 tn + l/2 R n t xm • Dark rings (destructive interference): dark centre ring 2 tn + l /2 = (m+1/2)l Therefore: • Bright rings (constructive interference): 2 tn + l /2 = ml Therefore: xm 2 = R 2 - (R-t)2 = R 2 - (R 2 -2 Rt+t 2) = 2 Rt -t 2 When R>>t then xm 2 ~ 2 Rt P 1 X: Optics, Waves and Lasers Lectures, 2005 -06. 8