Lecture 5 From Transition Amplitudes to Cross sections

Lecture 5: From Transition Amplitudes to Cross sections 0 Introduction to current particle physics 1 The Yukawa potential and transition amplitudes 2 Scattering processes and phase space 3 Feynman diagrams and QED 4 The weak interaction and the CKM matrix 5 CP violation and the B-factories 6 Neutrino masses and oscillations 7 Quantum chromodynamics (QCD) 8 Deep inelastic scattering, structure functions and scaling violations 9 Electroweak unification: the Standard Model and the W and Z boson 10 Electroweak symmetry breaking in the SM, Higgs boson 11 LHC experiments 1

Recap Lecture 3 We have seen how to calculate a “transition amplitude” or “matrix element”, which describes the probability of a single particle scattering from a potential, which we are modelling in terms of an exchange particle. It consists of a propagator corresponding to the exchange boson times the two coupling strengths of the scattering particles to the exchange bosons (“charges”). Neglecting spin: Today, we will relate this to the quantities we measure in particle physics: cross-sections, angular distributions, decay rates etc. 2

From Scattering Amplitudes to Transition Rates: Fermi’s Golden Rule Transition rate from initial to final states Tfi gives the probability of transition per unit time per target particle - See handout for derivation (beyond scope of course) - Dimensions = per unit time - - Scattering amplitude appears squared - = density of final states n – i. e. dn/d. E (aka “phase space”) … … number of available quantum mechanical final states in the energy interval between Ef and Ef+d. Ef is (Ef)d. Ef , where Ef is final state particle energy in the centre of mass frame. 3

From Transition Rates to Cross sections - Cross-sections express the strength of interaction: - Thinking in ‘fixed target’ mode, they express the effective area presented by the target to the projectile perpendicular to the beam direction (actually an integral of the reaction probability over all impact parameters with eg 1/r potential). - Since it is an area transverse to the beam, it is invariant under Lorentz boosts along the beam axis (i. e. same theory applies to collider mode) Units: 1 barn (1 b) = 10 -28 m 2 ~ physical size of a nucleus … more usefully in particle physics, mb, nb, pb, fb … 4

Cross Sections and Flux Factors e. g. Cross section s for the process AB CD (with B as fixed target) can be determined from experimentally measurable transition rate Gfi (AB CD) and flux of incoming particles of type A, f. A … with the usual relation to speed v. A of particles A and number n. A of particles A per unit volume For one particle per unit volume, Generalising to any frame, Although this is not Lorentz invariant, (sometimes known as Lorentz Invariant Flux Factor is … 5

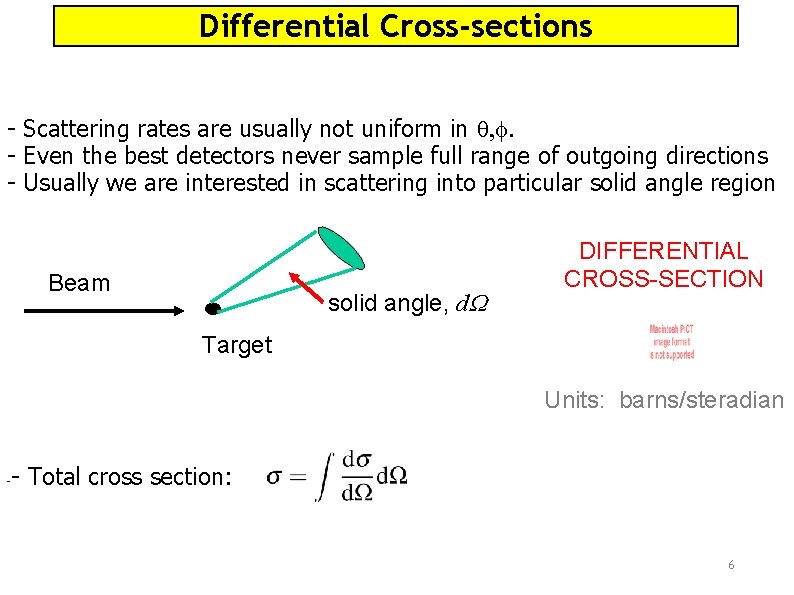
Differential Cross-sections - Scattering rates are usually not uniform in q, f. - Even the best detectors never sample full range of outgoing directions - Usually we are interested in scattering into particular solid angle region Beam solid angle, d. W DIFFERENTIAL CROSS-SECTION Target Units: barns/steradian - - Total cross section: 6

Phase space – A reminder Quantised particles in a cubic box … 2 a 2 a 2 a Number of final states in a unit volume with momenta in element d 3 p • Number of available final states for particles C, D scattered into momentum elements d 3 p. C d 3 p. D is … • … subject to the constraints that p. C+p. D=p. A+p. B and EC+ED=EA+EB 7

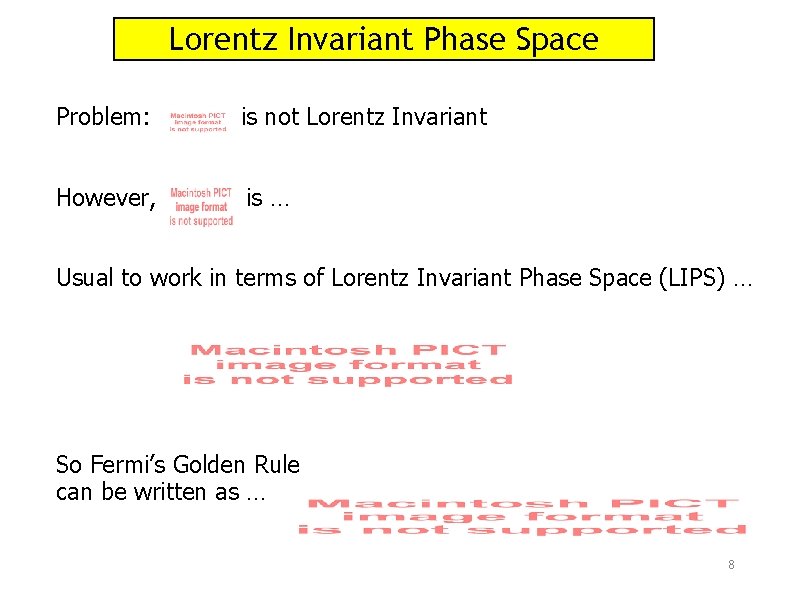
Lorentz Invariant Phase Space Problem: is not Lorentz Invariant However, is … Usual to work in terms of Lorentz Invariant Phase Space (LIPS) … So Fermi’s Golden Rule can be written as … 8

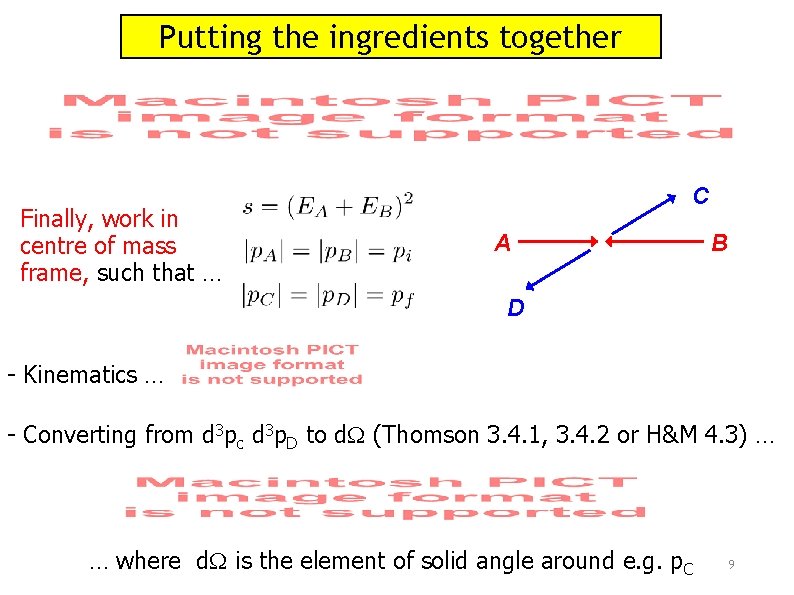
Putting the ingredients together Finally, work in centre of mass frame, such that … C A B D - Kinematics … - Converting from d 3 pc d 3 p. D to d (Thomson 3. 4. 1, 3. 4. 2 or H&M 4. 3) … … where d is the element of solid angle around e. g. p. C 9

Putting ingredients together 1/s dependence from kinematics … (accelerators need to increase luminosity to compensate for cross sections falling) Mfi contains all the physics dynamics … couplings and propagators Note that in the case of elastic scattering (AB=CD) or in the ultra-relativistic case where all particle masses are negligible, pf=pi Then … 10

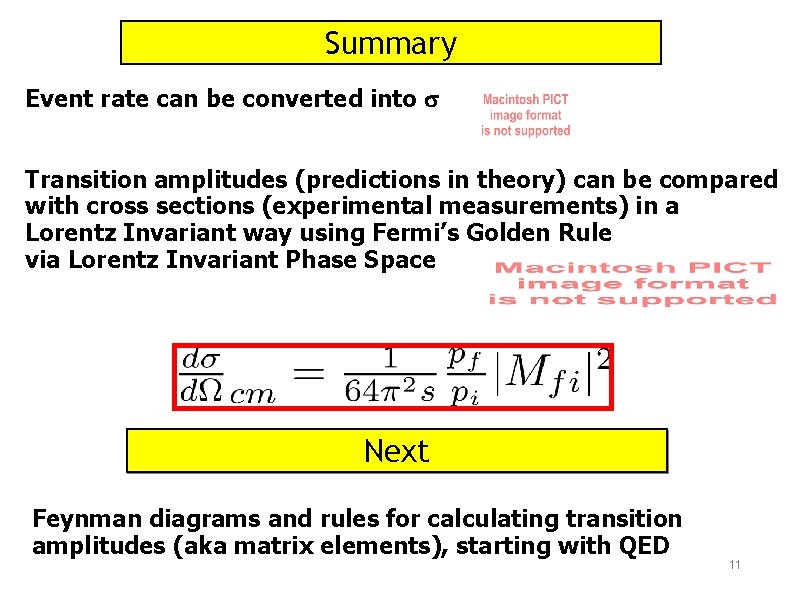
Summary Event rate can be converted into Transition amplitudes (predictions in theory) can be compared with cross sections (experimental measurements) in a Lorentz Invariant way using Fermi’s Golden Rule via Lorentz Invariant Phase Space Next Feynman diagrams and rules for calculating transition amplitudes (aka matrix elements), starting with QED 11