Lecture 5 Electromagnetic and Magnetic Circuit 1 Magnetic

Lecture 5 Electromagnetic and Magnetic Circuit 1

Magnetic & Magnetic Flux What is Magnet? ØAn object made of certain materials which create a magnetic field contains a north pole and south pole. ØMagnet flux leaves the magnet as the north pole and the place where the flux returns to the magnet as the south pole. Two types of magnet: • Permanent magnet • Electromagnet 2

Magnetic Field • Consists of the line of force, or flux lines that radiate from the north pole (N) to the south pole (S) and back to the north pole through the magnet material. • The strength of a magnetic field in a particular region is directly related to the density of flux lines in that region 3

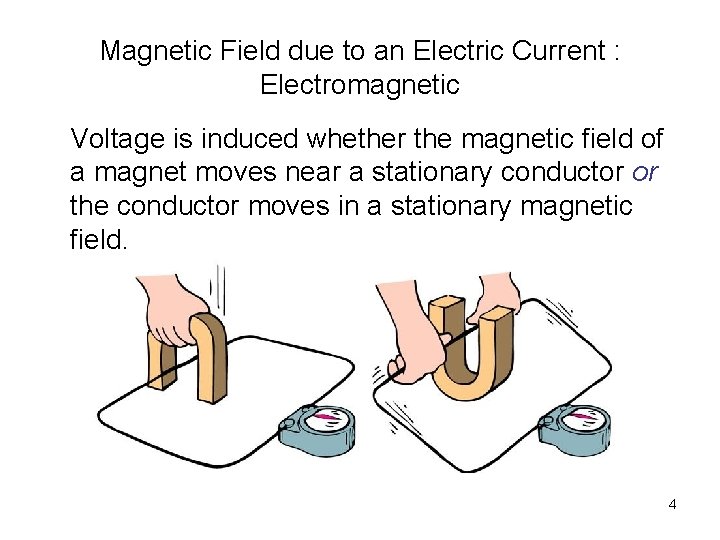
Magnetic Field due to an Electric Current : Electromagnetic Voltage is induced whether the magnetic field of a magnet moves near a stationary conductor or the conductor moves in a stationary magnetic field. 4

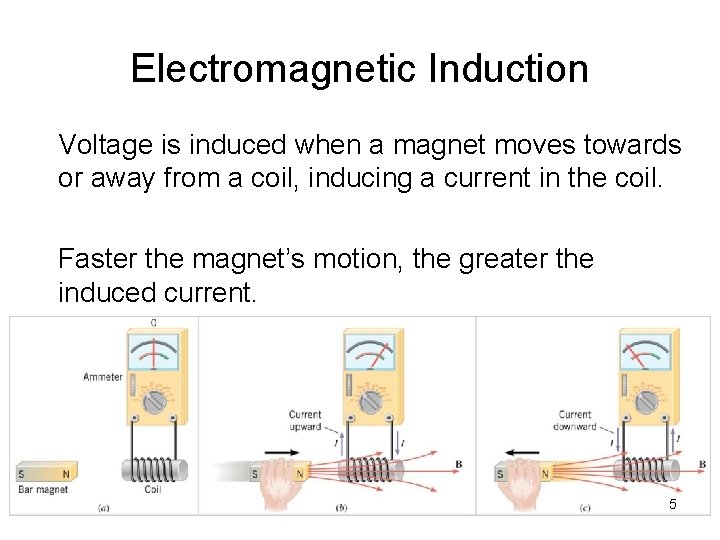
Electromagnetic Induction Voltage is induced when a magnet moves towards or away from a coil, inducing a current in the coil. Faster the magnet’s motion, the greater the induced current. 5

Application of Electromagnetic Induction : Magnetic Recording Write data by magnetizing recording media (e. g. , video tape, hard disk) using electromagnets. Data is read back using the induced current produced when magnetized media moves past receiver coils (reverse of writing data). Hard disk 6

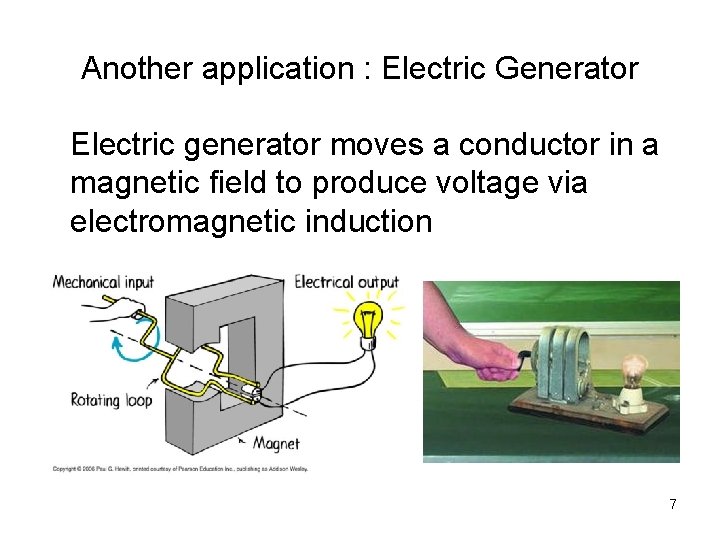
Another application : Electric Generator Electric generator moves a conductor in a magnetic field to produce voltage via electromagnetic induction 7

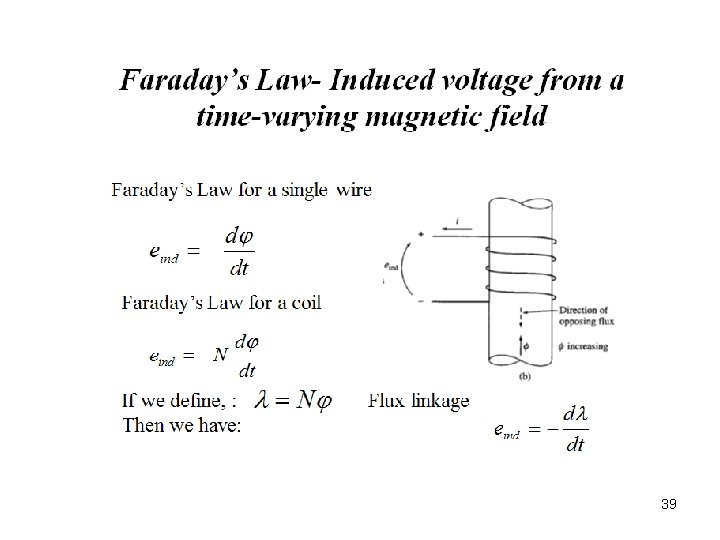
Faraday’s Law & Electromotive Force Faraday’s Law First Law It states that whenever the magnetic flux linked with a circuit changes, or whenever a conductor cuts magnetic flux, it induces an electromotive force (e. m. f). Second Law It states that the magnitude of induced e. m. f is equal to the rate of change of flux linkage. Electromotive Force Electromotive force is the electric potential (voltage) generated by either an electrochemical cell (battery) or a changing magnetic field. The SI unit for electromotive force is the volt. 8

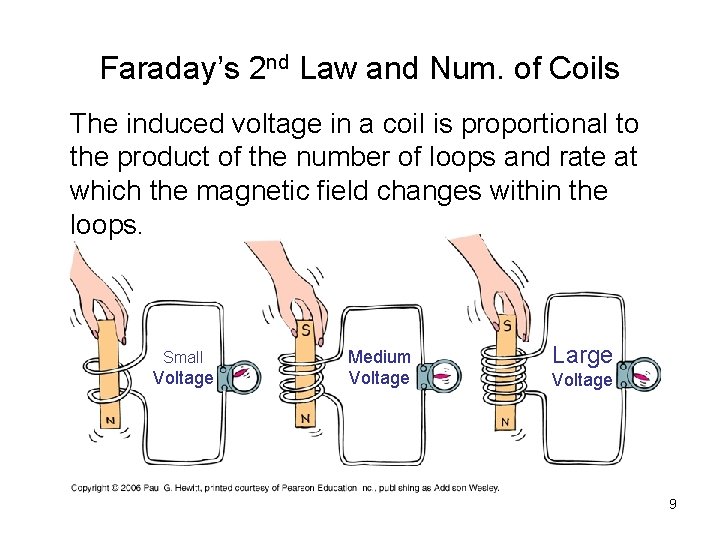
Faraday’s 2 nd Law and Num. of Coils The induced voltage in a coil is proportional to the product of the number of loops and rate at which the magnetic field changes within the loops. Small Voltage Medium Voltage Large Voltage 9

Example 1 Suppose a coil has 500 turns and flux through it, and changes from initial value of 0. 12 Wb (webers, unit of magnetic flux) to the final value of 0. 012 Wb in time 0. 02 second. Find the electromagnetic force induced in it. 10

Exercise 2 Apply Faraday's law to find the induced voltage across a coil with 500 turns that is located in a magnetic field that is changing at a rate of 8000 µWb/s. • Answer : 4. 0 V 11

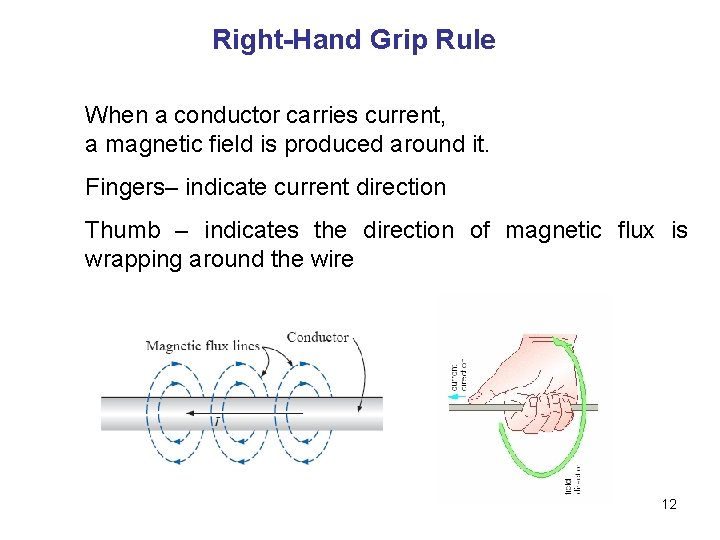
Right-Hand Grip Rule When a conductor carries current, a magnetic field is produced around it. Fingers– indicate current direction Thumb – indicates the direction of magnetic flux is wrapping around the wire 12

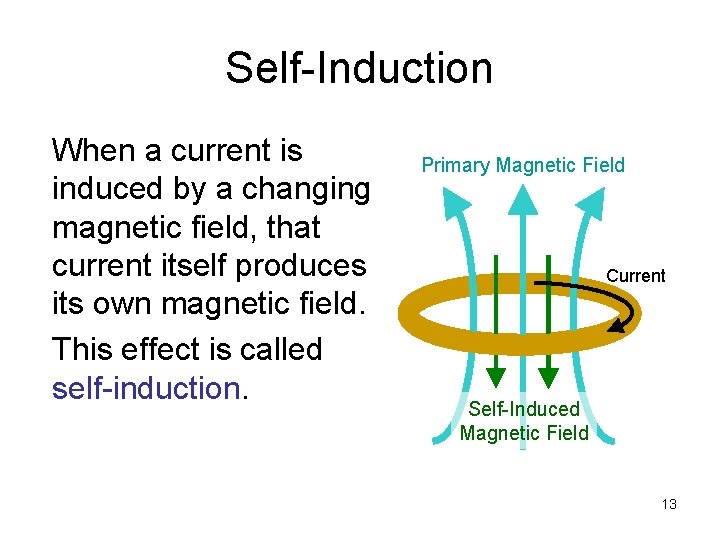
Self-Induction When a current is induced by a changing magnetic field, that current itself produces its own magnetic field. This effect is called self-induction. Primary Magnetic Field Current Self-Induced Magnetic Field 13

Application of Self-induction effect : Magnetic Brakes Strong magnet dropped into a copper pipe falls slowly due to secondary magnetic field induced by its motion. Great America’s Drop Zone has a 22 story freefall, lasting four seconds, decelerated by magnetic braking. 14

Lenz’s Law Ø Lenz’s Law states that the direction of any magnetic induction effect is such as to oppose the cause of the effect. Ø The “cause” may be changing flux q through a stationary circuit due to a changing Magnetic flux density, B of the field q due to motion of the conductors that make up the circuit Ø When the current through a coil changes, an induced voltage is created (induced e. m. f) as a result of the changing electromagnetic field and the polarity of the induced voltage is such that it always opposes the change in current (back e. m. f). 15

Magnetic Flux Density, B Ø Magnetic flux density is the amount of flux per unit area perpendicular to the magnetic field. Ø Symbol denoted by B, unit tesla (T). ØThe closer together the lines of flux, the stronger the field. That is, the strength of the field is represented by the density of the lines of flux. 16

Magnetomotive Force, Fm Ø Magnetomotive force (m. m. f) is a force that produces the magnetic field. Ø Unit as ampere-turn (At) Ø The magnetomotive force (m. m. f), Fm is proportional to the product of the number of turns around the core (in which the flux is to be established) and the current through the turns of wire 17

Magnetic Field Intensity, H Ø Magnetic Field Intensity, also knowns as Magnetizing force, H in a material is a Magnetomotive force per unit length of the material. Ø Unit : ampere–turns per meter (At/m) Ø H is depends on the number of turns of the coil of wire (N), current through coil (I) and length of material (l). 18

Reluctance, R Ø Magnetic reluctance, or magnetic resistance, R is a concept used in the analysis of magnetic circuits. R Ø It is analogous to resistance in an electrical circuit, but rather than dissipating electric energy, it stores magnetic energy. Ø Unit : ampere–turns per Weber (At/ Wb) R In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, permeability is the degree of magnetization that a material obtains in response to an applied magnetic field. Kebolehtelapan (permeability) adalah tahap kemagnetan yang dipunyai oleh sesuatu material sebagai tindak- balas terhadap medan magnet yang diberikan kepadanya. 19

Relationship between B-H Ø Flux density (B) and magnetizing force (H) are related by the equation However, relative permeability is So, μ 0 , permeability of free space 20 is given as 4π x 10 -7 Wb/At. m

Example 3 / Magnetizing Force 21

Example 4 • Determine the reluctance of a piece of mu-metal of length 150 mm and cross-sectional area 1800 mm 2 when the relative permeability is 4000. Find also the absolute permeability of the mu-metal. R Mu-metal is a nickel-iron alloy, composed of approximately 77% nickel, 16% iron, 5% copper and 2% chromium or molybdenum, that is notable for its high magnetic permeability. 22

Exercise 5 • Find the relative permeability of a material if the absolute permeability is 4. 084 x 10 -4 Wb/At. m (Answer : 325) Given, relative permeability of a medium μr is a ratio of absolute permeability relatively to the permeability of free space, μ 0 23

Magnetic Hysteresis Ø The phenomenon in which the value of a physical property lags behind changes in the effect causing it, as for instance when magnetic induction lags behind the magnetizing force. "This tendency to ‘remember their magnetic history’ is called hysteresis. “ Ø In other word, hysteresis is the lagging effect between the flux density, B of a material and the applied magnetizing force, H. “Hysteresis” adalah kesan ketinggalan (kelewatan yang berlaku) antara ketumpatan fluks pada sesuatu bahan (magnet) berbanding daya magnetizing yang diberikan kepadanya. 24

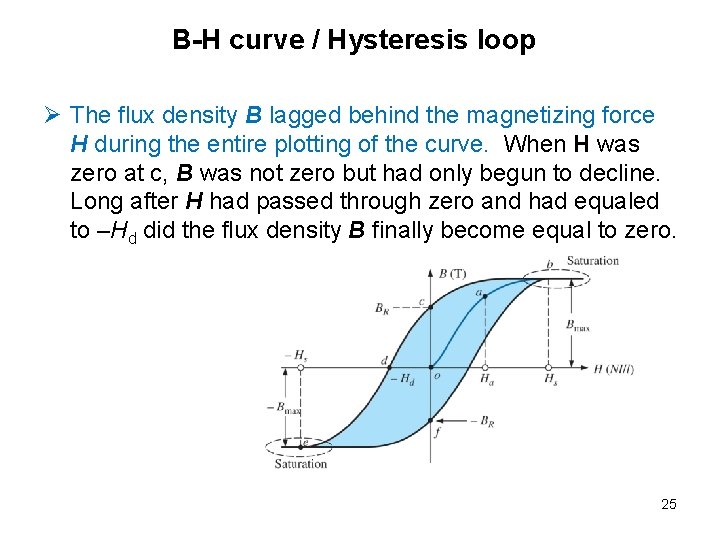
B-H curve / Hysteresis loop Ø The flux density B lagged behind the magnetizing force H during the entire plotting of the curve. When H was zero at c, B was not zero but had only begun to decline. Long after H had passed through zero and had equaled to –Hd did the flux density B finally become equal to zero. 25

MAGNETIC CIRCUIT A simple magnetic circuit having a ring shaped magnetic core (toroid) and a coil that extends around the entire circumference. When current i flows through the coil of N turns, a magnetic flux is produced. 26

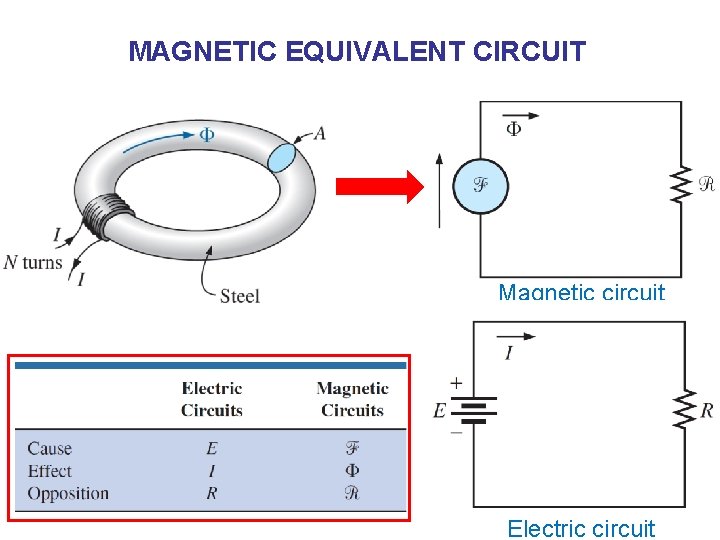
MAGNETIC EQUIVALENT CIRCUIT Magnetic circuit 27 Electric circuit

ANALOGY BETWEEN MAGNETIC CIRCUIT AND ELECTRIC CIRCUIT a) Magnetic equivalent circuit b) Electric equivalent circuit To solve magnetic equivalent circuit – Kirchhoff Voltage and Current Laws (KVL & KCL) Electric circuit Magnetic circuit Driving force e. m. f (E) m. m. f (F) Produces Current (i) Flux (Ф) Limited by Resistance (R) Reluctance (R) 28

Ampere’s Circuital Law Ø The algebraic sum of the rises and drops of the Magnetomotive force (m. m. f) around a closed loop of a magnetic circuit is equal to zero. or; Ø The sum of the rises in Magnemotive force (m. m. f) equals the sum of the drops in m. m. f around a closed loop. Similar to KVL in electric circuit R 29

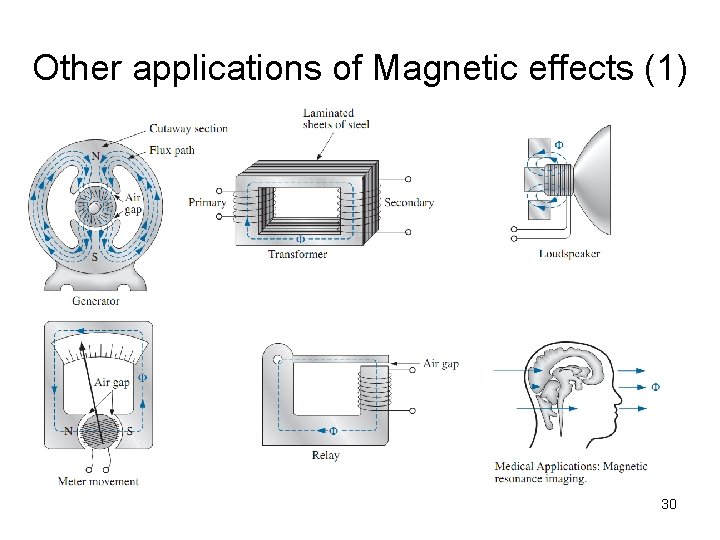
Other applications of Magnetic effects (1) 30

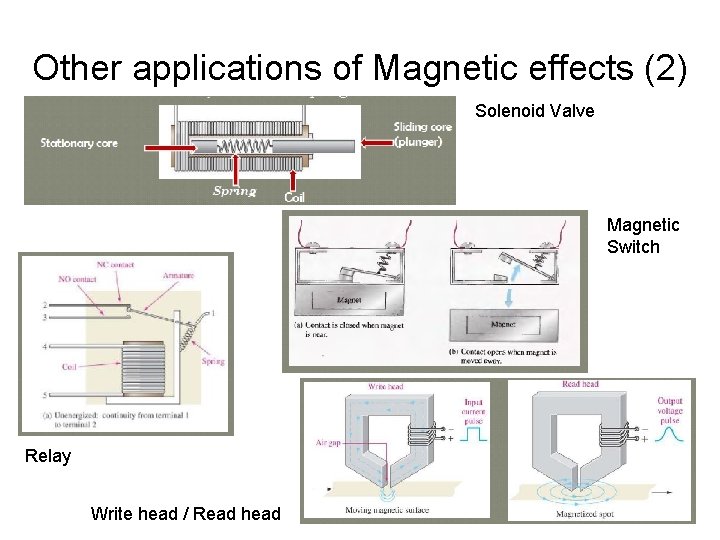
Other applications of Magnetic effects (2) Solenoid Valve Magnetic Switch Relay Write head / Read head 31

QUIZ 2 A coil of 400 turns is wound uniformly on a ring of nonmagnetic material. The ring has a mean circumference of 30 cm and a uniform cross-section area of 5 cm 2. If the current in the coil is 4 A. Given, for non-magnetic material, μr = 1. Calculate: 1. the magnetic field strength, H. 2. the flux density, B. 3. the total magnetic flux in the ring, Φ. 32

FRINGING EFFECT Fringing Effect: Bulging of the flux lines in the air gap. Effect: The effective cross section area of air gap increase so the reluctance of the air gap decrease. The flux density Bg < Bc, Bc is the flux density in the core. If the air gaps is small, the fringing effect can be neglected. So In practical, large air gap will be divided into several small air gaps to reduce the fringing effect. 33

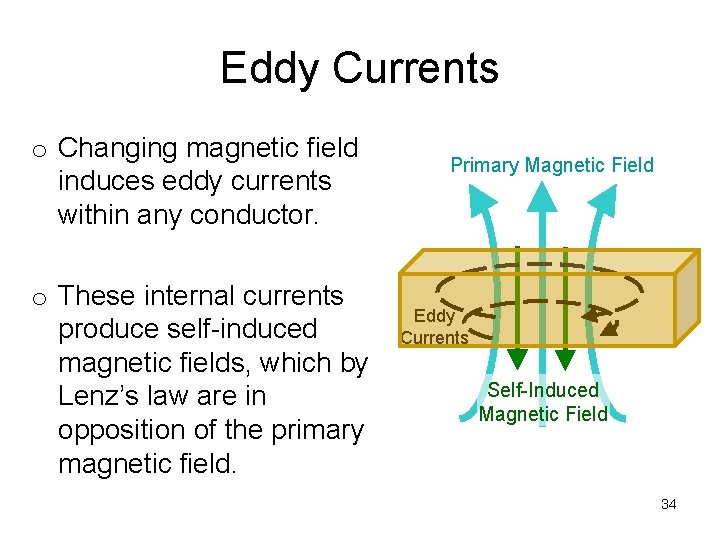
Eddy Currents o Changing magnetic field induces eddy currents within any conductor. o These internal currents produce self-induced magnetic fields, which by Lenz’s law are in opposition of the primary magnetic field. Primary Magnetic Field Eddy Currents Self-Induced Magnetic Field 34

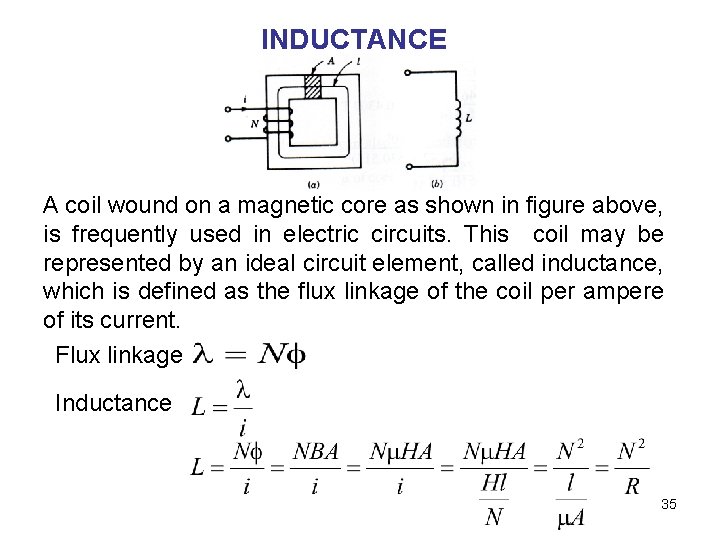
INDUCTANCE A coil wound on a magnetic core as shown in figure above, is frequently used in electric circuits. This coil may be represented by an ideal circuit element, called inductance, which is defined as the flux linkage of the coil per ampere of its current. Flux linkage Inductance 35

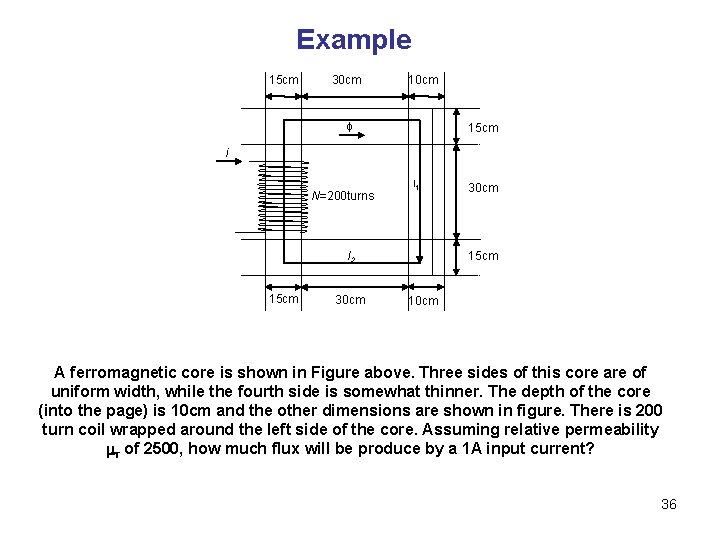
Example 15 cm 30 cm 15 cm i N=200 turns l 1 l 2 15 cm 30 cm 15 cm 10 cm A ferromagnetic core is shown in Figure above. Three sides of this core are of uniform width, while the fourth side is somewhat thinner. The depth of the core (into the page) is 10 cm and the other dimensions are shown in figure. There is 200 turn coil wrapped around the left side of the core. Assuming relative permeability mr of 2500, how much flux will be produce by a 1 A input current? 36

Solution Example The mean path length of region 1 is 45 cm and the cross-sectional area is 10 x 10 cm = 100 cm 2. Therefore, the reluctance in the first region is: The mean path length of region 2 is 130 cm and the cross-sectional area is 15 x 10 cm = 150 cm 2. Therefore, the reluctance in the second region is: 37

Solution Example Therefore, the total reluctance in the core is: The total magnetomotive force (MMF) is: The total flux in the core is given by: 38

39

40

41

42

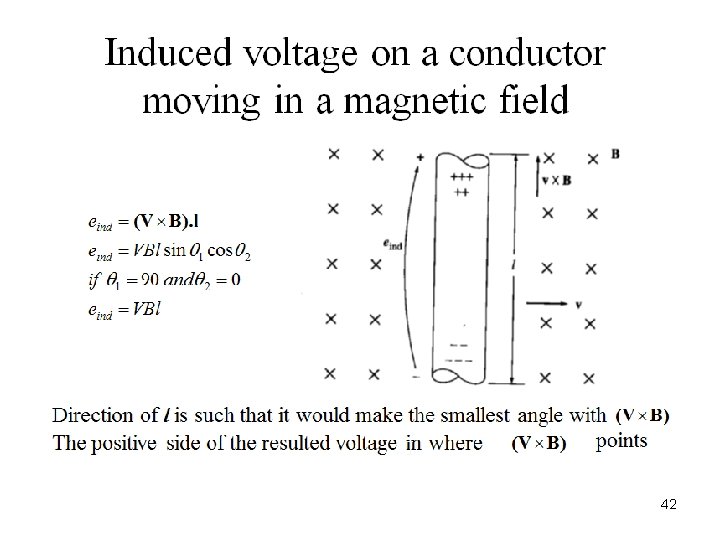
Induced Voltage on a Conductor moving in a magnetic field Example The wire is shown in figure 1 below is moving in the presence of a magnetic field. With the information given in the figure, determine the magnitude and direction of the induced voltage in the wire. 43

44