Lecture 5 Bayesian Posterior Uncertainty is different from

Lecture 5 Bayesian Posterior Uncertainty is different from randomness The future is completely uncertain… …I am completely certain of this

Outline • Historical note about Bayes’ rule • Manty Hall problem • Bayesian updating for failure strength • Bayesian updating for model parameter – Salary offer estimate • Coin trials example • Reading material: – Gelman, Andrew, et al. Bayesian data analysis. CRC press, 2003, Chapter 1. 2 Structural & Multidisciplinary Optimization Group

Historical Note • Birth of Bayesian – Rev. Thomas Bayes proposed Bayes’ theory (1763): q of Binomial dist. is estimated using observed data. Laplace discovered, put his name (1812), generalized to many prob’s. – For more than 100 years, Bayesian “degree of belief” was rejected as vague and subjective. Objective “frequency” was accepted in statistics. – Jeffreys (1939) rediscovered, made modern theory (1961). Until 80 s, still limited due to requirement for computation. • Flourishing of Bayesian – From 1990, rapid advance of HW & SW, made it practical. – Bayesian technique applied to areas of science (economics, medical) & engineering. 3 Structural & Multidisciplinary Optimization Group

Bayesian Probability • What is Bayesian probability ? – Classical: relative frequency of an event, given many repeated trials (e. g. , probability of throwing 10 with pair of dice) – Bayesian: degree of belief that it is true based on evidence at hand • Saturn mass estimation – Classical: mass is fixed but unknown – Bayesian: mass described probabilistically based on observations (e. g, uniformly in interval (a, b) 4 Structural & Multidisciplinary Optimization Group

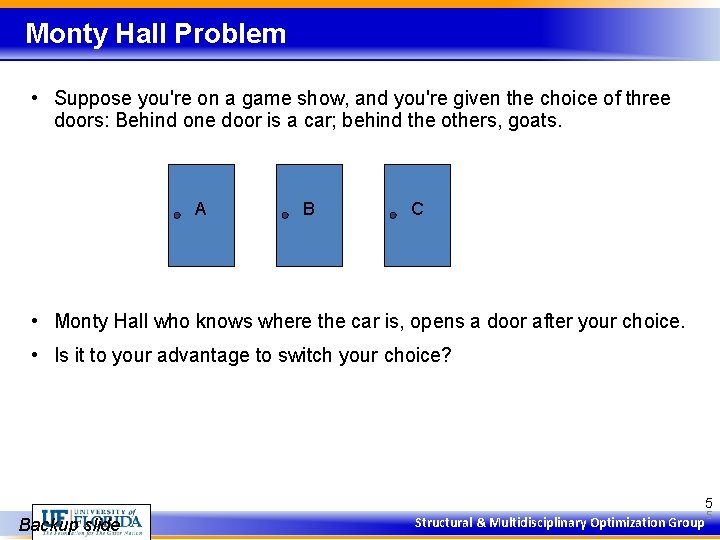
Monty Hall Problem • Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. A B C • Monty Hall who knows where the car is, opens a door after your choice. • Is it to your advantage to switch your choice? 5 Backup slide Structural & Multidisciplinary Optimization Group 5

Solution • Three possible scenarios • The player picked Goat A. The host shows the other goat. • The player picked Goat B. The host shows the other goat. • The player picked the car. The host picks one goat. • By Bayes’ theorem • The player picked A, host shows B Switching wins ! 6 Structural & Multidisciplinary Optimization Group 6

Likelihood • If the player picked A, then the host must reveal goat B. He cannot reveal car at C. • From the known information (host opened B), the likelihood of the car being at A is defined by • If the car is at A, then it is equally probable that the host shows B or C, so the likelihood is ½ • In the same way, the likelihood of the car being at C is defined by • Here the host do not have any option, he must open B, so the likelihood is 1. • Note that the sum of likelihood is not 1. In this case, it is 1 ½. Structural & Multidisciplinary Optimization Group 7 7

Bayes’ Rule (Review) • Probability Form • PDF Form • Since f. Y(y) can be considered as a normalizing constant • Often f. Y(y | x) is called likelihood function, L(y | x) • Use the property that the area under PDF = 1 Therefore, all questions boil down to the prior and likelihood Structural & Multidisciplinary Optimization Group 8

Bayesian Updating of Failure Strength • We want to estimate the uncertainty of normalized failure strength given 3 test data • Prior distribution of failure strength is uniformly distributed ~ U(0. 9, 1. 1) • 3 tensile tests yield measured failure strength of 1. 05, 1. 10, and 1. 15 • Test variability is uniformly distributed ~U(-0. 15, 0. 15) 7 prior 6 Since the prior is within the likelihood, the posterior = the prior 5 Likelihood 4 3 2 1 0 0. 95 1 1. 05 1. 15 1. 2 (a) Initial distribution and first test result 9 Structural & Multidisciplinary Optimization Group

Likelihood of Failure Strength • Representing test variability – Assume uniform distribution ~ U(test-0. 15, test+0. 15) • Likelihood L(test | x): – When true failure strength is x, the probability to get failure strength test a a x=0. 8: 0. 001: 1. 3; n=size(x, 2); f. Y(x) likelihood=zeros(1, n); prior=pdf('unif', x, 0. 9, 1. 1); x 1 a=0. 15; test 1=1. 05; for i=1: n likelihood(i)=pdf('unif', test 1, x(i)-a, x(i)+a); end posterior=prior. *likelihood; area=sum(posterior)*0. 001; posterior=posterior/area; plot(x, prior, x, likelihood, x, posterior); y x x 2 y 10 Structural & Multidisciplinary Optimization Group

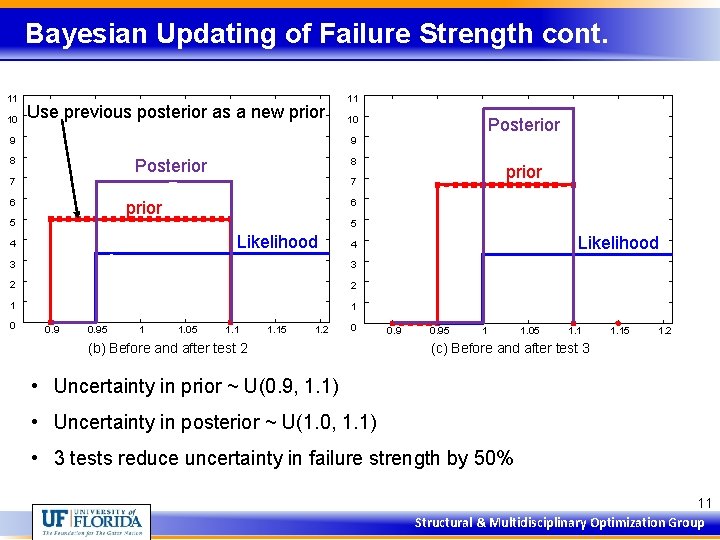
Bayesian Updating of Failure Strength cont. 11 10 Use previous posterior as a new prior 9 11 10 9 8 Posterior 8 7 prior 7 6 6 prior 5 5 Likelihood 4 3 2 2 1 1 0. 95 1 1. 05 1. 15 1. 2 Likelihood 4 3 0 Posterior 0 (b) Before and after test 2 0. 95 1 1. 05 1. 15 1. 2 (c) Before and after test 3 • Uncertainty in prior ~ U(0. 9, 1. 1) • Uncertainty in posterior ~ U(1. 0, 1. 1) • 3 tests reduce uncertainty in failure strength by 50% 11 Structural & Multidisciplinary Optimization Group

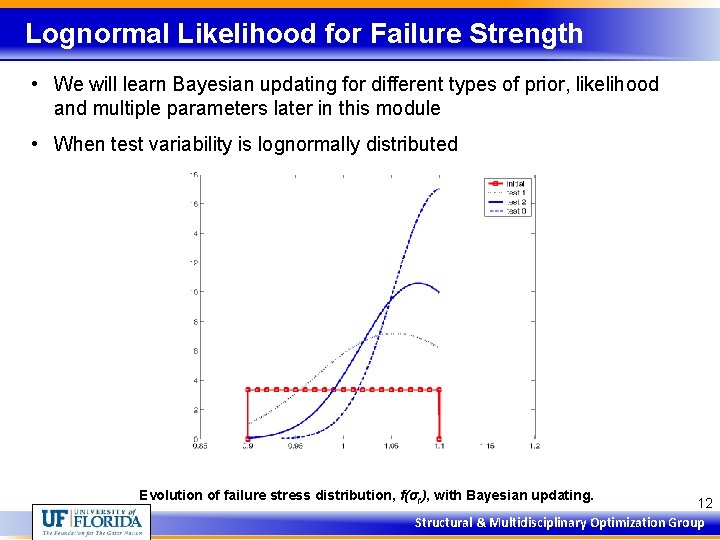
Lognormal Likelihood for Failure Strength • We will learn Bayesian updating for different types of prior, likelihood and multiple parameters later in this module • When test variability is lognormally distributed Evolution of failure stress distribution, f(σf), with Bayesian updating. 12 Structural & Multidisciplinary Optimization Group

Normal Likelihood • If the error is assumed to have a fixed standard deviation, the likelihood for this error will be calculated from pdf of normal distribution • In the same way as uniform, normal likelihood is constructed as follows 7 for i=1: n likelihood(i)=. . . pdf(‘norm', test 1, mean, std); end Posterior 6 prior 5 4 Likelihood 3 2 1 0 0. 85 0. 95 1 1. 05 1. 15 1. 25 1. 3 13 Structural & Multidisciplinary Optimization Group

Exercise • Possible Scenarios – Prior uncertainty is increased from 10% to 15% – Test variability is increased from 15% to 20% 14 Structural & Multidisciplinary Optimization Group

Bayesian Updating for Model Parameters • Previous example is Bayesian updating of a distribution when the same data are observed • Most engineering applications have a mathematical model, but the model parameters q are unknown (uncertain) • We want to identify (update) model parameters q using test data y • Different from least squares because parameters are given as a distribution Prior distribution Likelihood function Posterior distribution Updated prior PDF Observed data added 15 Structural & Multidisciplinary Optimization Group

Salary Estimate Example • You are considering an engineering position for which salary offers θ (in thousand dollars) have recently followed the triangular distribution • Your friend received a $93 K offer for a similar position, and you know that their range of offers for such positions is no more than $5 K. • Before your friend’s data, what was your chance of an offer <$93 K? • Estimate the distribution of the expected offer and the likeliest value. 16 Structural & Multidisciplinary Optimization Group

Self Evaluation Question • What value of salary offer to your friend would leave you with the least uncertainty about your own expected offer? 17 Structural & Multidisciplinary Optimization Group

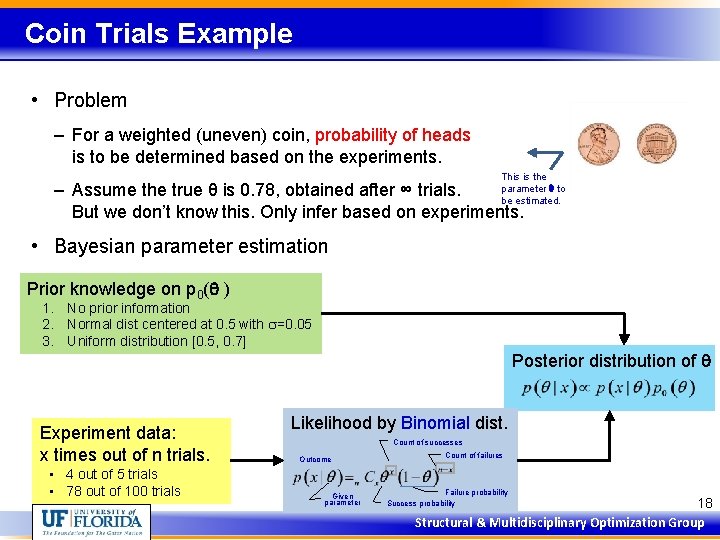
Coin Trials Example • Problem – For a weighted (uneven) coin, probability of heads is to be determined based on the experiments. This is the parameter q to be estimated. – Assume the true θ is 0. 78, obtained after ∞ trials. But we don’t know this. Only infer based on experiments. • Bayesian parameter estimation Prior knowledge on p 0(q ) 1. No prior information 2. Normal dist centered at 0. 5 with s=0. 05 3. Uniform distribution [0. 5, 0. 7] Experiment data: x times out of n trials. • 4 out of 5 trials • 78 out of 100 trials Posterior distribution of q Likelihood by Binomial dist. Count of successes Outcome Given parameter Count of failures Failure probability Success probability 18 Structural & Multidisciplinary Optimization Group

Coin Trial Example • MATLAB code dx=0. 01; x=0. 0: dx: 1. 0; n=size(x, 2); likelihood=zeros(1, n); prior=pdf('unif', x, 0. 0, 1. 0); for i=1: n theta=(i-1)*dx; likelihood(i)=pdf('bino', 78, 100, theta); end posterior=prior. *likelihood; area=sum(posterior)*dx; posterior=posterior/area; plot(x, prior, x, likelihood, x, posterior); 19 Structural & Multidisciplinary Optimization Group

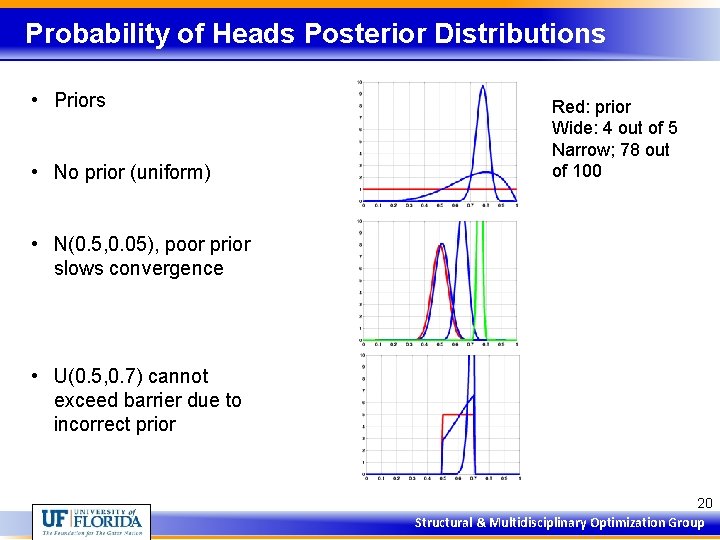
Probability of Heads Posterior Distributions • Priors • No prior (uniform) Red: prior Wide: 4 out of 5 Narrow; 78 out of 100 • N(0. 5, 0. 05), poor prior slows convergence • U(0. 5, 0. 7) cannot exceed barrier due to incorrect prior 20 Structural & Multidisciplinary Optimization Group

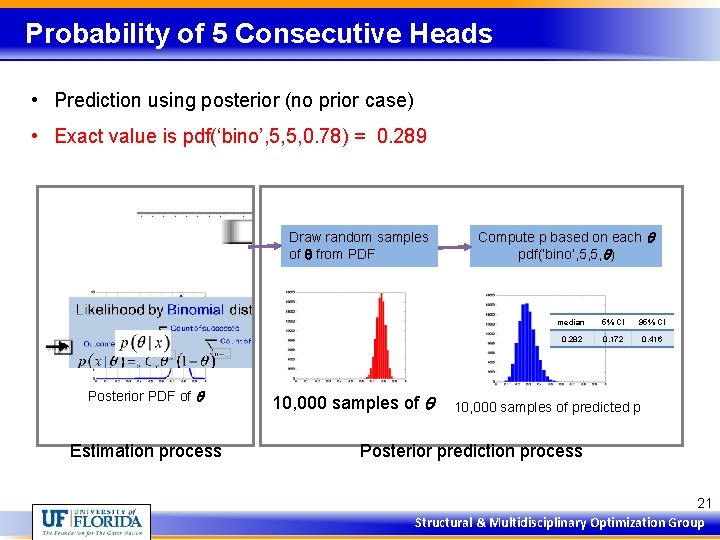
Probability of 5 Consecutive Heads • Prediction using posterior (no prior case) • Exact value is pdf(‘bino’, 5, 5, 0. 78) = 0. 289 Draw random samples of q from PDF Posterior PDF of q Estimation process 10, 000 samples of q Compute p based on each q pdf(‘bino’, 5, 5, q) median 5% CI 95% CI 0. 282 0. 172 0. 416 10, 000 samples of predicted p Posterior prediction process 21 Structural & Multidisciplinary Optimization Group

Practice Problems • For the salary estimate problem, what is the probability of getting a better offer than your friend? • For the salary problem, calculate the 95% confidence bounds on your salary around the mean and median of your expected salary distribution. • Slide 20 shows the risks associated with using a prior. When is it important to use a prior? 22 Structural & Multidisciplinary Optimization Group