Lecture 5 Barometric formula and the Boltzmann equation

Lecture 5 Barometric formula and the Boltzmann equation (continued) Notions on Entropy and Free Energy Intermolecular interactions: Electrostatics

Barometric formula because pressure is proportional to the number of particles p~n n = number of particles per unit volume normalizing to the volume c = n/V c = concentration (which is probability) Boltzmann: in our case U is constant because T is constant

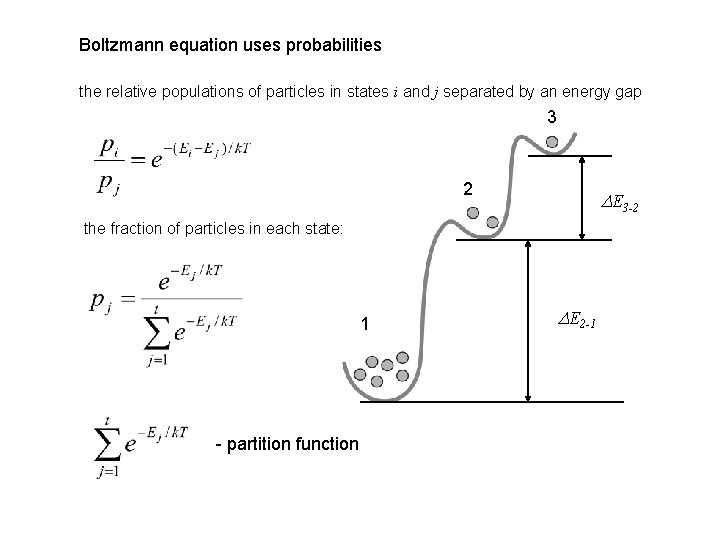
Boltzmann equation uses probabilities the relative populations of particles in states i and j separated by an energy gap 3 2 DE 3 -2 the fraction of particles in each state: 1 - partition function DE 2 -1

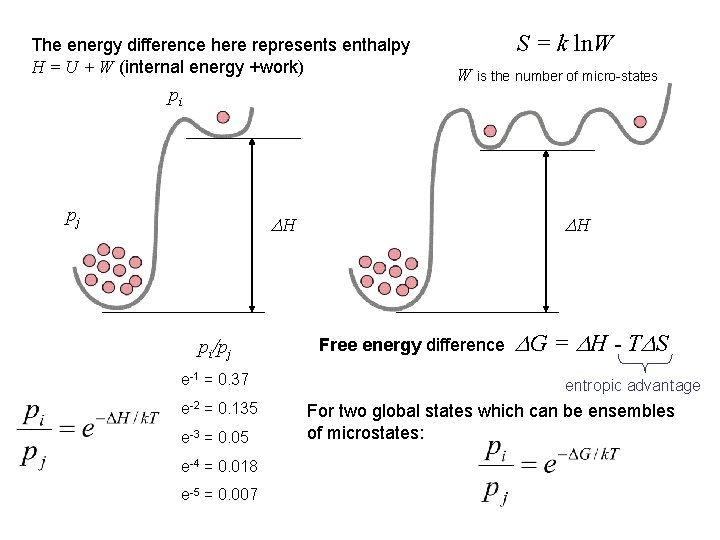
The energy difference here represents enthalpy H = U + W (internal energy +work) pi pj S = k ln. W W is the number of micro-states DH pi/pj e-1 = 0. 37 e-2 = 0. 135 e-3 = 0. 05 e-4 = 0. 018 e-5 = 0. 007 DH Free energy difference D G = D H - TD S entropic advantage For two global states which can be ensembles of microstates:

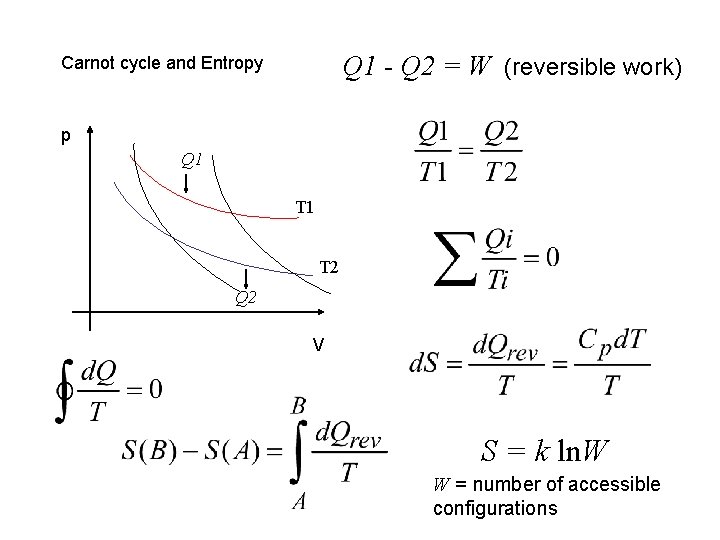
Q 1 - Q 2 = W (reversible work) Carnot cycle and Entropy p Q 1 T 2 Q 2 V S = k ln. W W = number of accessible configurations

At constant T Helmholtz Free Energy

Helmholtz Free Energy Gibbs Free Energy

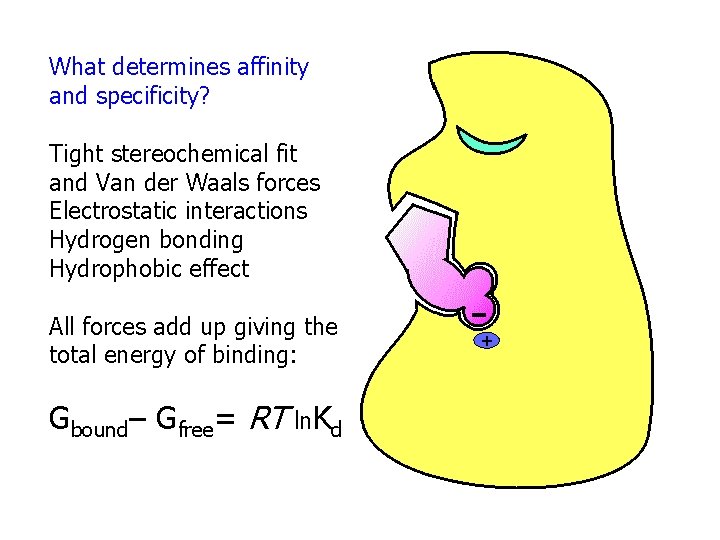
What determines affinity and specificity? Tight stereochemical fit and Van der Waals forces Electrostatic interactions Hydrogen bonding Hydrophobic effect All forces add up giving the total energy of binding: Gbound– Gfree= RT ln. Kd

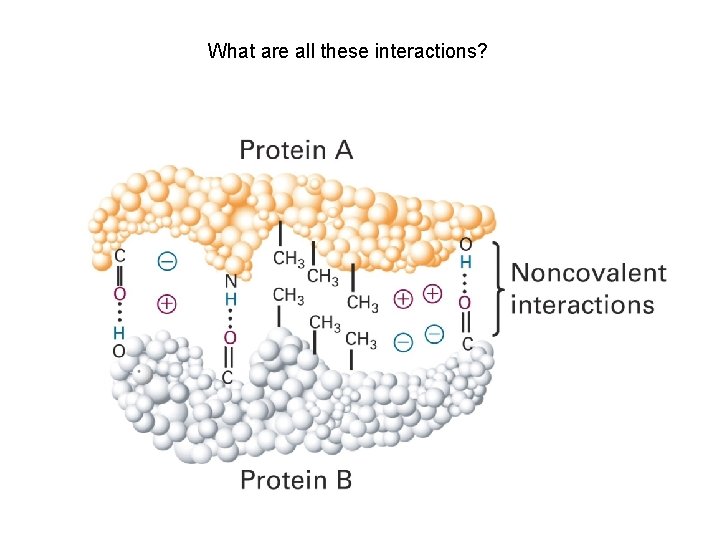
What are all these interactions?

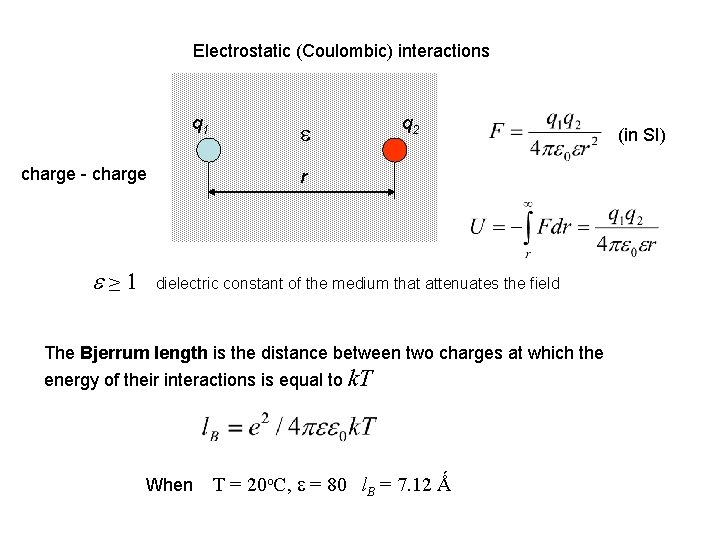
Electrostatic (Coulombic) interactions q 1 charge - charge e≥ 1 e q 2 r dielectric constant of the medium that attenuates the field The Bjerrum length is the distance between two charges at which the energy of their interactions is equal to k. T When T = 20 o. C, e = 80 l. B = 7. 12 Ǻ (in SI)

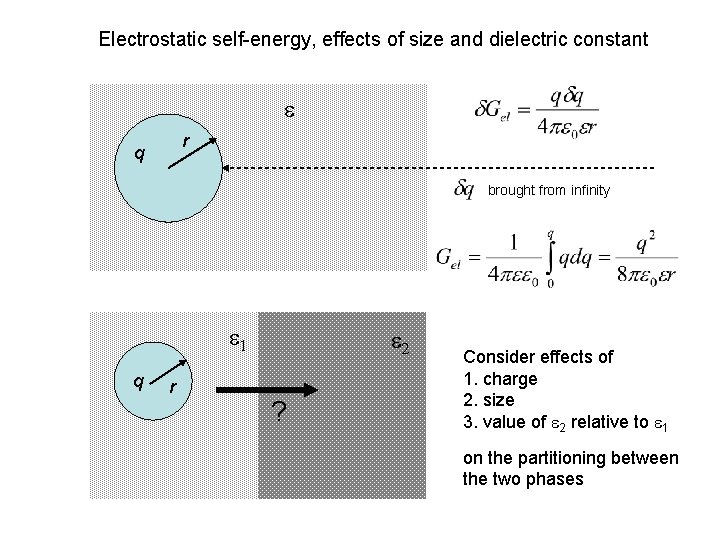
Electrostatic self-energy, effects of size and dielectric constant e r q brought from infinity e 1 q r e 2 ? Consider effects of 1. charge 2. size 3. value of e 2 relative to e 1 on the partitioning between the two phases

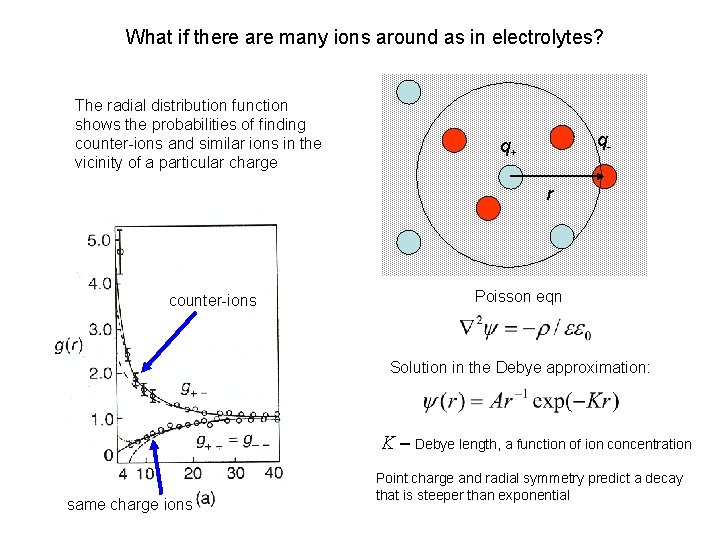
What if there are many ions around as in electrolytes? The radial distribution function shows the probabilities of finding counter-ions and similar ions in the vicinity of a particular charge q- q+ r counter-ions Poisson eqn Solution in the Debye approximation: K – Debye length, a function of ion concentration same charge ions Point charge and radial symmetry predict a decay that is steeper than exponential

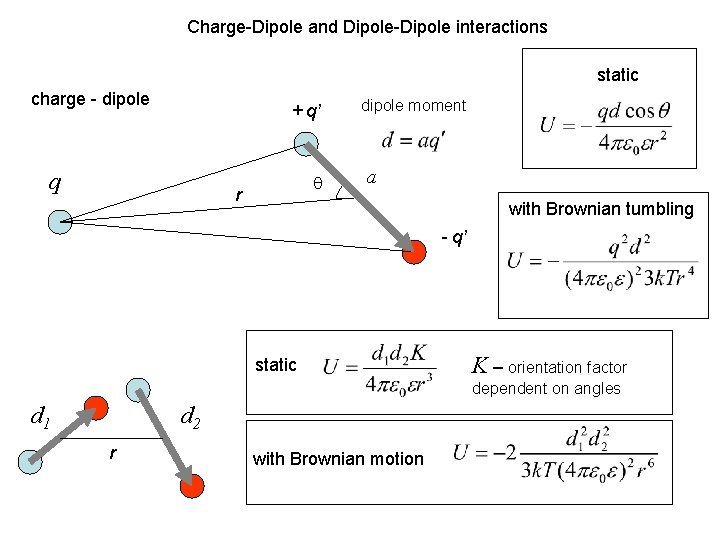
Charge-Dipole and Dipole-Dipole interactions static charge - dipole + q’ q q r dipole moment a with Brownian tumbling - q’ static K – orientation factor dependent on angles d 1 d 2 r with Brownian motion

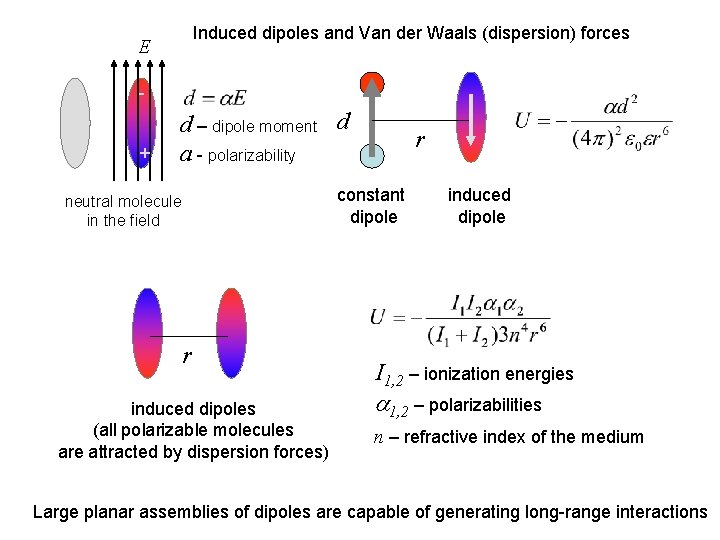
Induced dipoles and Van der Waals (dispersion) forces E + d – dipole moment d a - polarizability neutral molecule in the field r induced dipoles (all polarizable molecules are attracted by dispersion forces) r constant dipole induced dipole I 1, 2 – ionization energies a 1, 2 – polarizabilities n – refractive index of the medium Large planar assemblies of dipoles are capable of generating long-range interactions

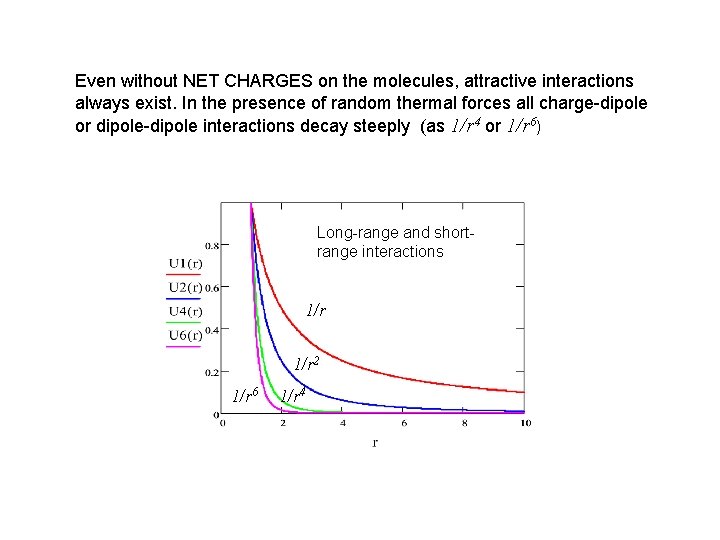
Even without NET CHARGES on the molecules, attractive interactions always exist. In the presence of random thermal forces all charge-dipole or dipole-dipole interactions decay steeply (as 1/r 4 or 1/r 6) Long-range and shortrange interactions 1/r 2 1/r 6 1/r 4

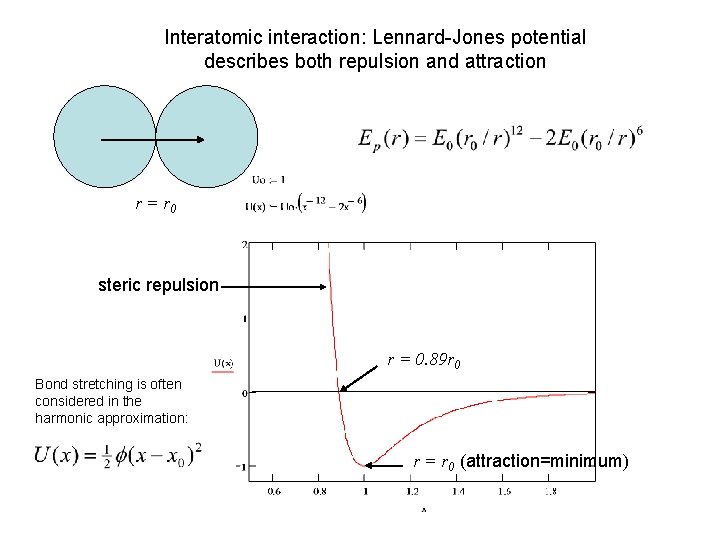
Interatomic interaction: Lennard-Jones potential describes both repulsion and attraction r = r 0 steric repulsion r = 0. 89 r 0 Bond stretching is often considered in the harmonic approximation: r = r 0 (attraction=minimum)

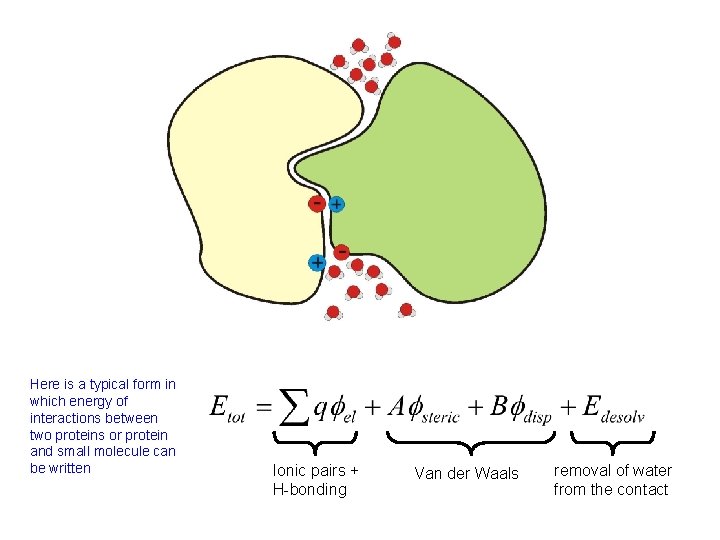
Here is a typical form in which energy of interactions between two proteins or protein and small molecule can be written Ionic pairs + H-bonding Van der Waals removal of water from the contact