Lecture 40 WHAT IS IT THAT WEVE LEARNED

Lecture 40 WHAT IS IT THAT WE’VE LEARNED?

1. Linear systems

Linear systems Any linear algebra problem boils down to solving a linear system. For nonlinear problems, there is a way to approximate them via linear systems (linear approximation in Calc I is the first step in this direction) and extract some valuable information about the system (for instance, is the system stable? Lyapunov’s theory, Control theory, etc. , need more math courses). The point is: there abundant in science and are fundamental. Questions. 1 How to solve one? It’s not difficult to produce an algorithm, but one needs to employ specifics of the problem and techniques from numerical analysis if one needs an effective algorithm (need to take more courses). Basic algorithm: Gaussian elimination The idea from the very beginning: it’s easy to solve a system if it has a “staircase pattern” (back substitution). For a general system, we aim at transforming it to a system that does follow the pattern, and the procedure is called row reduction.

Linear systems 2 How to analyze one? 2. 1 What’s the minimum number of equations that still have the same solutions? Answer: Rank = the minimum number of equations that still have the same solutions. Example. Recall a problem from the last exam:

Now compute the eigenspaces. For instance, Wait… Understanding of rank and nullity helps reducing the complexity of a problem and tells something about the structure of solutions (next slides)

Linear systems 2. 2 Ok, but how to determine which equations form that minimum set? Possible answers: 1. Use row reduction. The rows that are left form the minimum independent set of equations. (we’ve had a terminology for this: the corresponding rows form a basis of the row space of the matrix) 2. (not covered) There’s a way to determine the equations via studying minors of the matrix. 3. Use the specifics of a given problem.

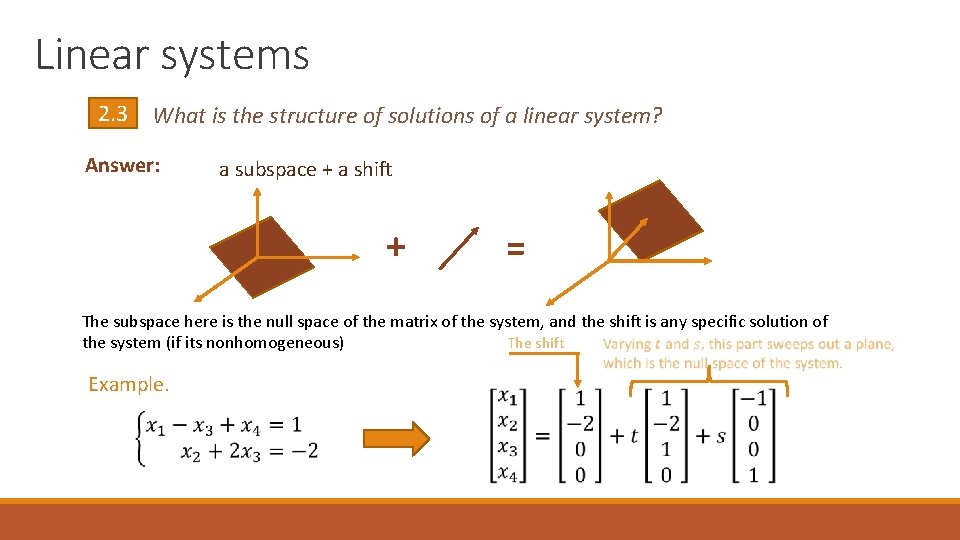
Linear systems 2. 3 What is the structure of solutions of a linear system? Answer: a subspace + a shift + = The subspace here is the null space of the matrix of the system, and the shift is any specific solution of The shift the system (if its nonhomogeneous) Example.

Linear systems 2. 3. 1 How big is that subspace? And how to determine its size? Answer-Question. What’s the proper way of measuring a subspace? Answer. The dimension is the size, and for linear systems it’s the nullity of the system. 2. 3. 2 Why is it useful to know? The better you know your enemy, the better you can fight it! Answer. For instance, since we know what the structure is, we can split the problem of finding solutions into two simpler ones: (that’ll be that shift)

2. Inconsistent systems

Inconsistent systems 1 How? (the best possible approximation) (We’ve seen that these systems naturally arise when one wants to find a geometric object that best fits some data; one can see the sequel of the story in statistics-related courses) (the same system after a series of manipulations; it’s easier to handle)

3. Vectors and linear transformations

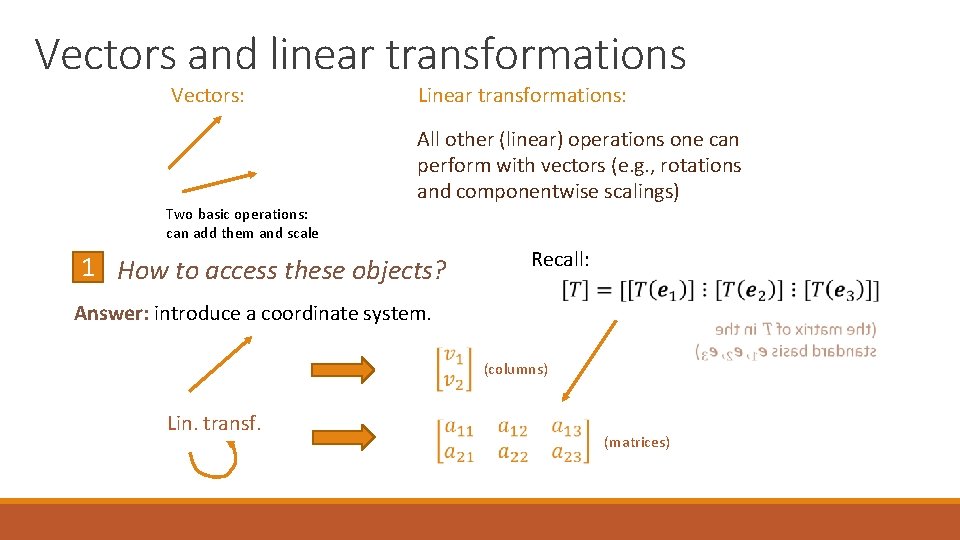
Vectors and linear transformations Vectors: Two basic operations: can add them and scale Linear transformations: All other (linear) operations one can perform with vectors (e. g. , rotations and componentwise scalings) 1 How to access these objects? Recall: Answer: introduce a coordinate system. (columns) Lin. transf. (matrices)

Vectors and linear transformations What’s important: the correspondence is set up so that all operations are preserved: (and the same with the addition of linear operators and scaling)

Vectors and linear transformations 2 How to switch to a different coordinate system? Answer: use change-of-basis matrices. For instance, 2. 1 How to find these matrices? Way 1: Way 2: Apply Gauss-Jordan: (row reduction)

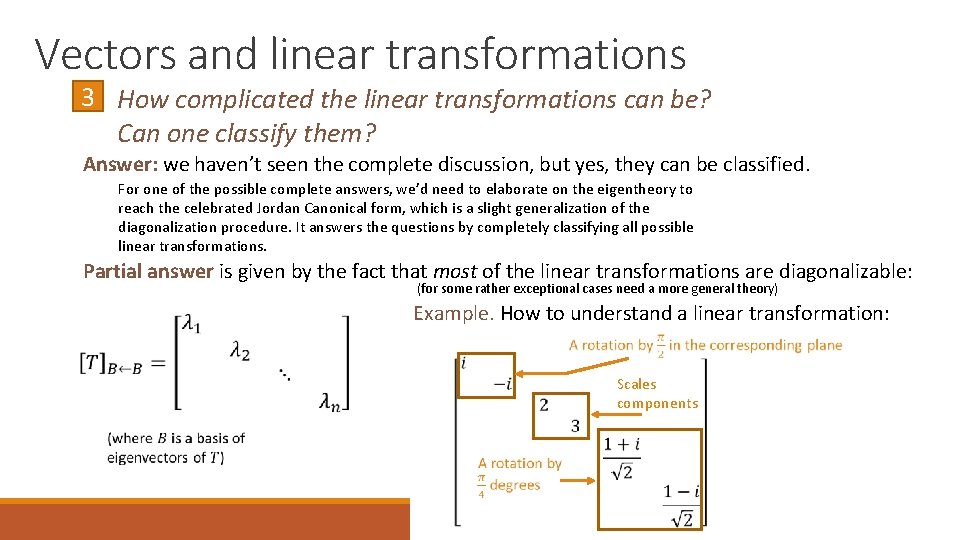
Vectors and linear transformations 3 How complicated the linear transformations can be? Can one classify them? Answer: we haven’t seen the complete discussion, but yes, they can be classified. For one of the possible complete answers, we’d need to elaborate on the eigentheory to reach the celebrated Jordan Canonical form, which is a slight generalization of the diagonalization procedure. It answers the questions by completely classifying all possible linear transformations. Partial answer is given by the fact that most of the linear transformations are diagonalizable: (for some rather exceptional cases need a more general theory) Example. How to understand a linear transformation: Scales components

Vectors and linear transformations 3. 1 How to find the diagonalization? Answer. 1. Compute all eigenvalues; 2. Compute all eigenspaces; 3. Form a basis of the space from the eigenvectors; 4. Find the matrix of the linear transformation in the basis of the eigenvectors. 3. 1. 1 How to compute the eigendata? Answer. First, need theory of determinants, which yields an equation for eigenvalues.

Vectors and linear transformations Digression into determinants For larger dimensions, use cofactor expansion or a row reduction. The crucial property: And the inverse exists if and only if the null space is trivial.

Vectors and linear transformations 3. 1. 1 How to compute the eigendata? To diagonalize, use the formula

Vectors and linear transformations 3. 2 How do we know if a linear transformation is diagonalizable? Answer. The criteria is: In general, An example of a non-diagonalizable matrix to keep it mind: (recall one of the previous exam questions)

4. Vector spaces

Vector spaces 1 Why care? Because linear algebra is applicable not only to vectors & columns but also to functions, operators, polynomials, etc. For instance, the modern treatment of quantum mechanics relies on this generalization. A vector space consists of objects that one can add and scale. We only need these two operations to be properly defined in order to apply linear algebra methods. Example. Functions and operators form vector spaces. Vectors Lin. transf. (what we might have in vector spaces in place of the usual vectors and linear transformations)

Vector spaces 2 How does it help? 1 We used linear algebra to understand linear differential equations: Linear algebra tells us that (exactly as for linear systems!) The linear differential operator on the LHS of the equation: 2 (not covered) With linear algebra, we can also understand systems like