Lecture 4 Regular Expressions 2004 SDU Regular expressions

Lecture 4 Regular Expressions 2004 SDU

Regular expressions A third way to view regular languages. Say that R is a regular expression if R is 1. 2. 3. 4. 5. 6. a, for some a in the alphabet , , (R 1 R 2) where R 1 and R 2 are regular expressions (R 1*) where R 1 is a regular expression The value of a regular expression is a language. § § § The value of ((0 1)*) is { s | s is any string of 0 and 1} Operation order: parenthesis, star, concatenation, union Note that this is an inductive definition! 2004 SDU 2

Language described by a regular expression Notation: L(r), or r, denotes the language described by regular expression r, define L( ) = L(a) = {a} L( ) = { } L( ) = L( ) L( *) = (L( ))* 2004 SDU 3

Examples of regular expressions Note: We drop parentheses when not required. § Example: (a b) is written a b Let = {a, b} The following are regular expressions: § § , a, b *, a*, b*, ab, a b, a* // is dropped (a b)*, a*b*, (ab)* (a b)*ab, etc. Are the following regular expressions? § a= , *a, a*b See page 65 example 1. 27 2004 SDU 4

Regular expression vs. Regular language A language is regular if and only if some regular expression describes it. Theorem: § (a) If a language is described by a regular expression, then it is regular. § (b) If a language is regular, then it is described by a regular expression. 2004 SDU 5

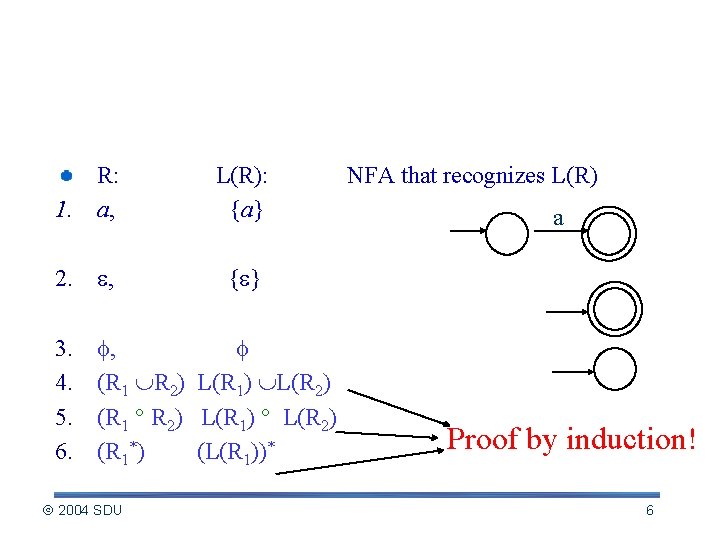
Regular expression NFA --proof of a R: 1. a, L(R): {a} 2. , { } 3. 4. 5. 6. , (R 1 R 2) L(R 1) L(R 2) (R 1 R 2) L(R 1) L(R 2) (R 1*) (L(R 1))* 2004 SDU NFA that recognizes L(R) a Proof by induction! 6

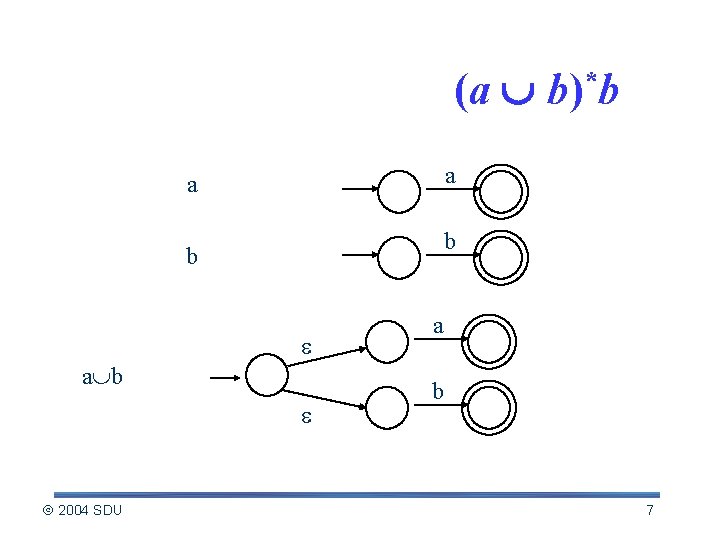
Example: NFA for (a b)*b a a b b a b 2004 SDU a b 7

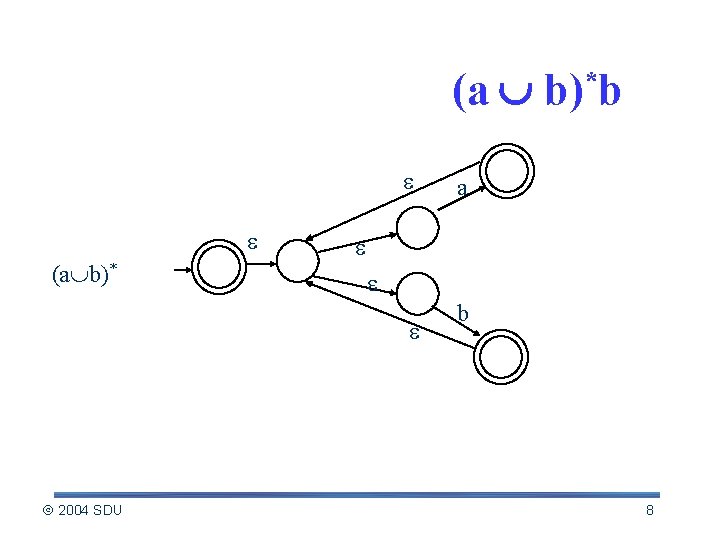
Example: NFA for (a b)*b (a b)* 2004 SDU a b 8

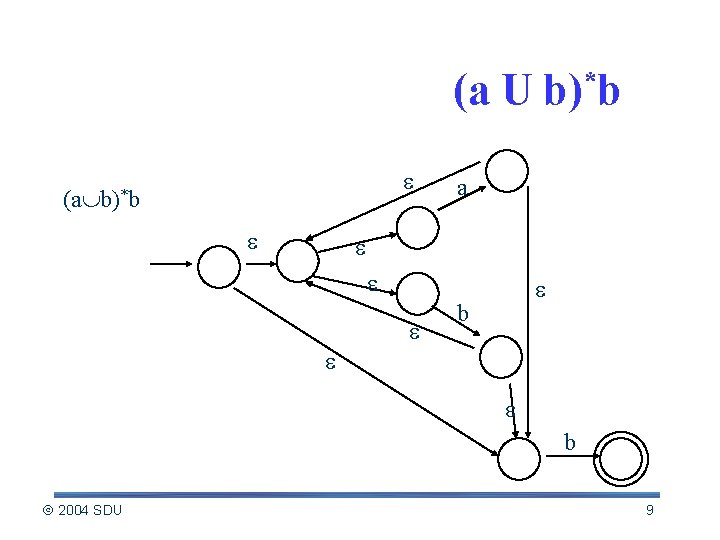
Example: NFA for (a U b)*b (a b)*b a b b 2004 SDU 9

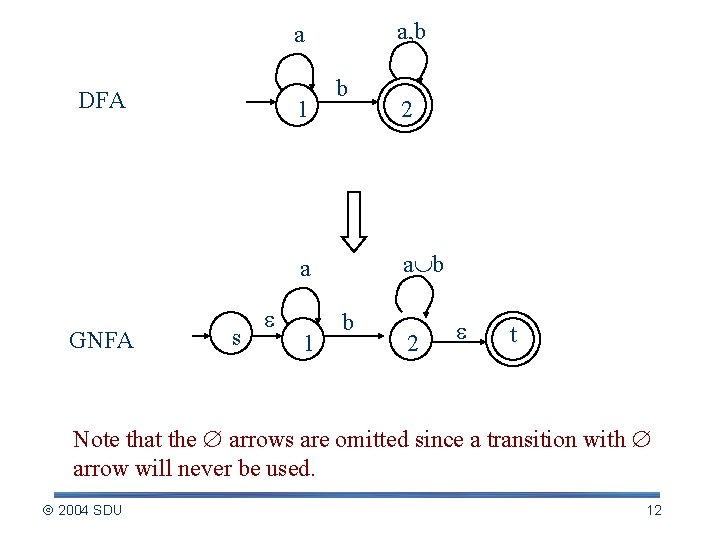
DFA regular expression --proof of b Easier to do: § DFA GNFA regular expression. GNFA (Generalized NFA) § A GNFA G = (Q, , , qstart, qaccept): 1. 2. 3. 4. 5. Q is the finite set of states, is the input alphabet, : (Q-{qaccept}) (Q-{qstart}) R is the transition function, qstart is the start state, and qaccept is the accept state, which is different from qstart. where R is the collection of regular expressions over . 2004 SDU 10

DFA regular expression --proof of b A GNFA accepts a string w in * if w = w 1 w 2…wk, where each wi is in * and a sequence of states q 0, q 1, …, qk exists such that 1. q 0=qstart is the start state 2. qk=qaccept is the accept state 3. For each i, we have wi L(Ri), where Ri= (qi-1, qi), i. e. , Ri is the expression on the arrow from qi-1 to qi. § From a DFA D to a GNFA M: § § § Add an extra start state s and an extra accept state t From s to the old start state add an arrow From the old accept states to t add arrows Multiple labels or arrows are replaced by single arrow labeled by the union of the labels Add arrows labeled between states with no arrows D and M recognize the same language. 2004 SDU 11

a, b a DFA 1 b a GNFA s 1 2 b 2 t Note that the arrows are omitted since a transition with arrow will never be used. 2004 SDU 12

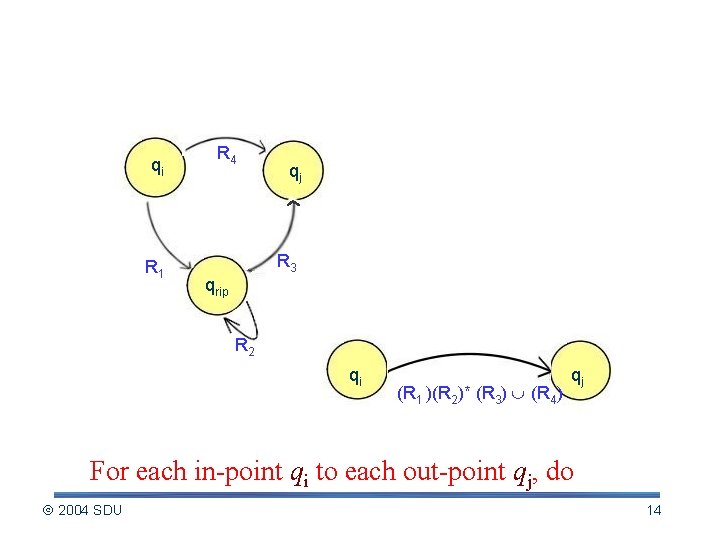
DFA regular expression (contd. ) Idea: § Convert DFA special GNFA. § Convert GNFA regular expression: – Eliminate all states, except start and accept state, one state at a time. – Output the label on the single transition left at the end. 2004 SDU 13

Eliminating state q{rip} qi R 1 R 4 qj R 3 qrip R 2 qi (R 1 )(R 2)* (R 3) (R 4) qj For each in-point qi to each out-point qj, do 2004 SDU 14

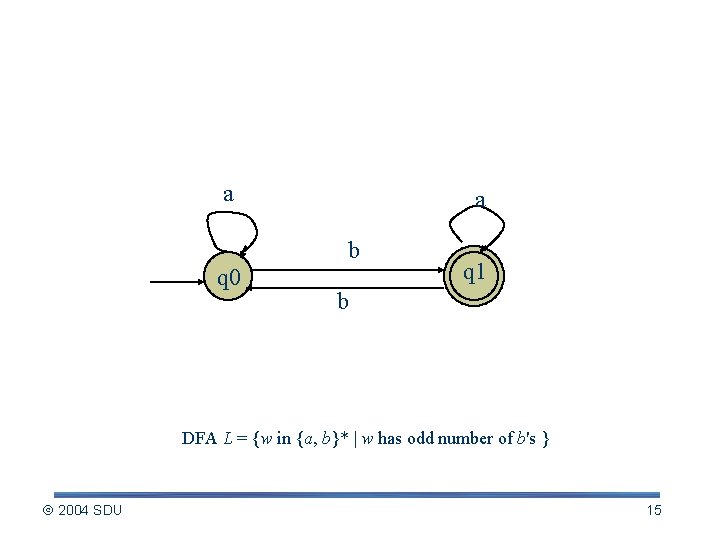
Constructing regular expression. a a b q 0 q 1 b DFA L = {w in {a, b}* | w has odd number of b's } 2004 SDU 15

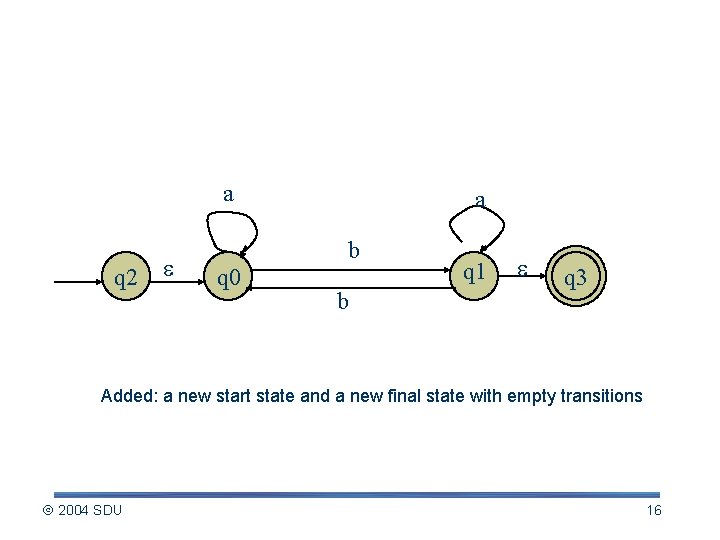
Constructing regular expression (contd. ) a q 2 a b q 0 b q 1 q 3 Added: a new start state and a new final state with empty transitions 2004 SDU 16

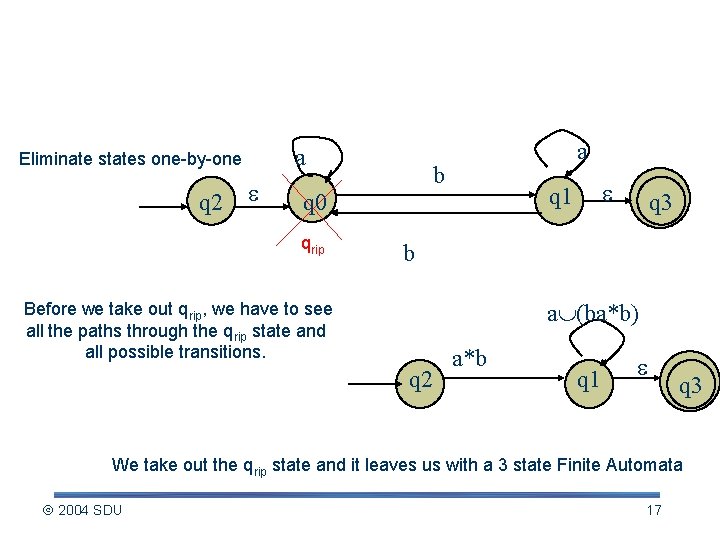
Constructing regular expression (contd. ) a Eliminate states one-by-one q 2 a b qrip q 1 q 0 q 3 b Before we take out qrip, we have to see all the paths through the qrip state and all possible transitions. a (ba*b) q 2 a*b q 1 q 3 We take out the qrip state and it leaves us with a 3 state Finite Automata 2004 SDU 17

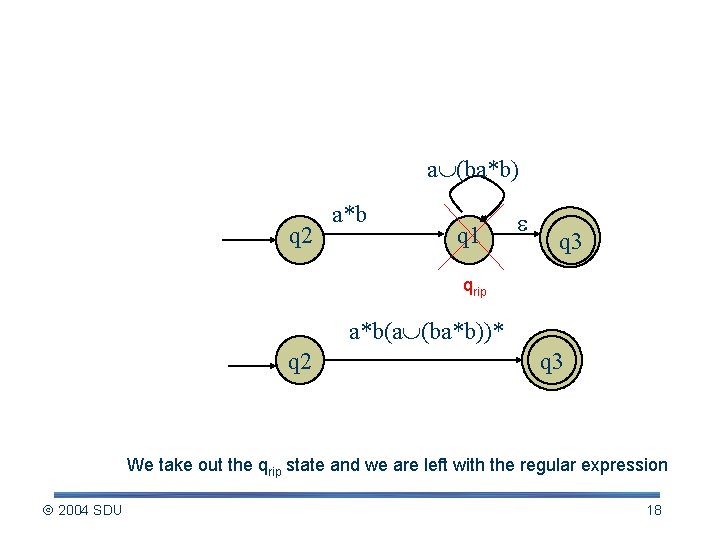
Constructing regular expression (contd. ) a (ba*b) q 2 a*b q 1 q 3 qrip a*b(a (ba*b))* q 2 q 3 We take out the qrip state and we are left with the regular expression 2004 SDU 18

Regular language vs regular expression Conclusion: Regular expressions exactly describe the class of regular languages. § E. g. , – – – 2004 SDU (0 1)*1 strings ending with 1 (00)* (000)* strings of multiple of 2 or 3 0’s ((0 1)1)* strings in which every even position is 1 (0 1)*111 ((0 1)* strings that contain 111 as substring … 19

More Exercises: 1. 18, 1. 19 2004 SDU 20