Lecture 4 Recursive Definitions CS 200 Computer Science

Lecture 4: Recursive Definitions CS 200: Computer Science David Evans University of Virginia 24 January 2003 CS 200 Spring 2003 http: //www. cs. virginia. edu/evans Computer Science

Menu • Defining Recursive Procedures • Problem Set 1 • Problem Set 2 24 January 2003 CS 200 Spring 2003 2

Defining Recursive Procedures 1. Be optimistic. – Assume you can solve it. – If you could, how would you solve a bigger problem. 2. Think of the simplest version of the problem, something you can already solve. (This is the base case. ) 3. Combine them to solve the problem. 24 January 2003 CS 200 Spring 2003 3

Example Define (find-closest goal numbers) that evaluates to the number in the list numbers list that is closest to goal: > (find-closest 200 (list 101 110 120 201 340 588)) 201 > (find-closest 12 (list 1 11 21)) 11 > (find-closest 12 (list 95)) 95 24 January 2003 CS 200 Spring 2003 4

Find Closest Number Be optimistic! Assume you can define: (find-closest-number goal numbers) that finds the closest number to goal from the list of numbers. What if there is one more number? Can you write a function that finds the closest number to match from new-number and numbers? 24 January 2003 CS 200 Spring 2003 5

Find Best Match Strategy: If the new number is better, than the best match with the other number, use the new number. Otherwise, use the best match of the other numbers. 24 January 2003 CS 200 Spring 2003 6

Optimistic Function (define (find-closest goal numbers) (if (< (abs (- goal (first numbers))) (abs (- goal (find-closest goal (rest numbers))))) (first numbers) (find-closest goal (rest numbers)))) 24 January 2003 CS 200 Spring 2003 7

Defining Recursive Procedures 2. Think of the simplest version of the problem, something you can already solve. If there is only one number, that is the best match. 24 January 2003 CS 200 Spring 2003 8

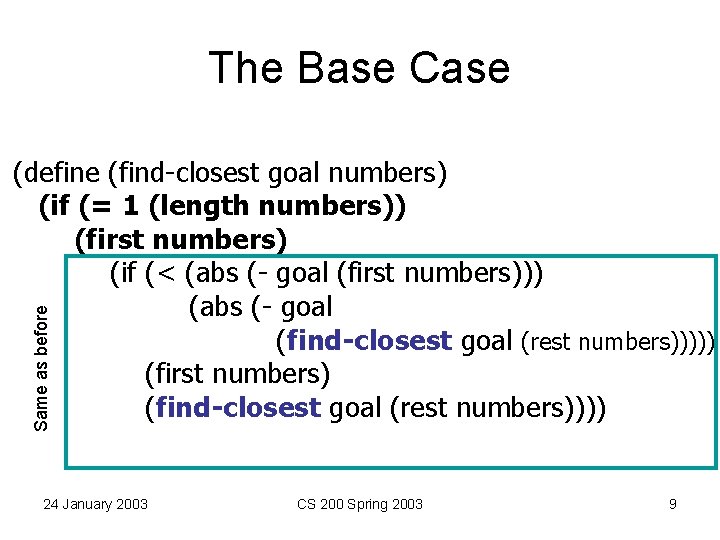
The Base Case Same as before (define (find-closest goal numbers) (if (= 1 (length numbers)) (first numbers) (if (< (abs (- goal (first numbers))) (abs (- goal (find-closest goal (rest numbers))))) (first numbers) (find-closest goal (rest numbers)))) 24 January 2003 CS 200 Spring 2003 9

Testing (define (find-closest goal numbers) (if (= 1 (length numbers)) (first numbers) (if (< (abs (- goal (first numbers))) (abs (- goal (find-closest goal (rest numbers))))) (first numbers) (find-closest goal (rest numbers)))) > (find-closest-number 200 (list 101 110 120 201 340 588)) 201 > (find-closest-number 0 (list 1)) 1 > (find-closest-number 0 (list )) first: expects argument of type <non-empty list>; given () 24 January 2003 CS 200 Spring 2003 10

Seen Anything Like This? (define (find-best-match sample tiles color-comparator) (if (null? tiles) ; ; ; If there are no tiles, (error "No tiles to match!") ; ; ; we must lose. (if (= (length tiles) 1) ; ; ; If there is just one tile, (first tiles) ; ; ; that tile is the best match. (pick-better-match ; ; ; Otherwise, the best match is sample ; ; ; either the first tile in tiles, (first tiles) ; ; ; or the best match we would find (find-best-match ; ; ; from looking at the rest of the sample ; ; ; tiles. Use pick-better-match (rest tiles) ; ; ; to determine which one is better. color-comparator)))) 24 January 2003 CS 200 Spring 2003 11

Fibonacci’s Problem Filius Bonacci, 1202 in Pisa: Suppose a newly-born pair of rabbits, one male, one female, are put in a field. Rabbits mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits. Suppose that our rabbits never die and that the female always produces one new pair (one male, one female) every month from the second month on. How many pairs will there be in one year? 24 January 2003 CS 200 Spring 2003 12

Rabbits From http: //www. mcs. surrey. ac. uk/Personal/R. Knott/Fibonacci/fibnat. html 24 January 2003 CS 200 Spring 2003 13

Fibonacci Numbers GEB p. 136: These numbers are best defined recursively by the pair of formulas FIBO (n) = FIBO (n – 1) + FIBO (n – 2) for n > 2 FIBO (1) = FIBO (2) = 1 Can we turn this into a Scheme function? Note: SICP defines Fib with Fib(0)= 0 and Fib(1) = 1 for base case. Same function except for Fib(0) is undefined in GEB version. 24 January 2003 CS 200 Spring 2003 14

Defining Recursive Procedures Slide 3 Returns… 1. Be optimistic. – Assume you can solve it. – If you could, how would you solve a bigger problem. 2. Think of the simplest version of the problem, something you can already solve. (This is the base case. ) 3. Combine them to solve the problem. 24 January 2003 CS 200 Spring 2003 15

Defining FIBO 1. Be optimistic - assume you can solve it, if you could, how would you solve a bigger problem. 2. Think of the simplest version of the problem, something you can already solve. 3. Combine them to solve the problem. 24 January 2003 These numbers are best defined recursively by the pair of formulas FIBO (n) = FIBO (n – 1) + FIBO (n – 2) for n > 2 FIBO (1) = FIBO (2) = 1 CS 200 Spring 2003 16

Defining fibo ; ; ; (fibo n) evaluates to the nth Fibonacci ; ; ; number (define (fibo n) FIBO (1) = FIBO (2) = 1 (if (or (= n 1) (= n 2)) 1 ; ; ; base case FIBO (n) = FIBO (n – 1) (+ (fibo (- n 1)) + FIBO (n – 2) (fibo (- n 2))))) for n > 2 24 January 2003 CS 200 Spring 2003 17

Fibo Results > (fibo 2) 1 Why can’t our > (fibo 3) 100, 000 x Apollo 2 Guidance > (fibo 4) 3 Computer calculate > (fibo 10) (fibo 100)? 55 > (fibo 100) Still working after 4 hours… To be continued Monday (answer is in SICP, 1. 2) 24 January 2003 CS 200 Spring 2003 18

Problem Set 1 24 January 2003 CS 200 Spring 2003 19

Question 2 • Without Evaluation Rules, Question 2 was “guesswork” • Now you know the Evaluation Rules, you can answer Question 2 without any guessing! 24 January 2003 CS 200 Spring 2003 20

2 d (100 + 100) Evaluation Rule 3. Application. a. Evaluate all the subexpressions 100 <primitive: +> 100 b. Apply the value of the first subexpression to the values of all the other subexpressions Error: 100 is not a procedure, we only have apply rules for procedures! 24 January 2003 CS 200 Spring 2003 21

2 h (if (not "cookies") "eat" "starve") Evaluation Rule 4 -if. Evaluate Expression 0. If it evaluates to #f, the value of the if expression is the value of Expression 2. Otherwise, the value of the if expression is the value of Expression 1. Evaluate (not "cookies") 24 January 2003 CS 200 Spring 2003 22

Evaluate (not "cookies") Evaluation Rule 3. Application. a. Evaluate all the subexpressions <primitive: not> “cookies” The quotes really matter here! Without them what would cookies evaluate to? b. Apply the value of the first subexpression to the values of all the other subexpressions (not v) evaluates to #t if v is #f, otherwise it evaluates to #f. (SICP, p. 19) So, (not “cookies”) evaluates to #f 24 January 2003 CS 200 Spring 2003 23

Defining not (not v) evaluates to #t if v is #f, otherwise it evaluates to #f. (SICP, p. 19) (define (not v) (if v #f #t) 24 January 2003 CS 200 Spring 2003 24

2 h (if (not "cookies") "eat" "starve") Evaluation Rule 4 -if. Evaluate Expression 0. If it evaluates to #f, the value of the if expression is the value of Expression 1. Otherwise, the value of the if expression is the value of Expression 2. Evaluate (not "cookies") => #f So, value of if is value of Expression 2 => “starve” 24 January 2003 CS 200 Spring 2003 25

Making Orange Ed Mitchell’s Answer (slightly adapted) (define (mix-one f a b) (/ (+ (f a) (f b)) 2)) (define (mix-color 1 color 2) (make-color (mix-one get-red color 1 color 2) (mix-one get-green color 1 color 2) (mix-one get-blue color 1 color 2))) 24 January 2003 CS 200 Spring 2003 26

Making Orange (define orange (mix-color red yellow)) (show-color orange) (define reddish-orange (mix-color red orange)) (show-color reddish-orange) 24 January 2003 CS 200 Spring 2003 27

brighter? Chalermpong Worawannotai’s answer (define (brightness color) (+ (get-red color) (get-green color) (get-blue color))) (define (brighter? color 1 color 2) (> (brightness color 1) (brightness color 2))) 24 January 2003 CS 200 Spring 2003 28

closer-color? (define (closer-color? sample color 1 color 2) (< (+ (abs (- (get-red color 1) (get-red sample))) (abs (- (get-blue color 1) (get-blue sample))) (abs (- (get-green color 1) (get-green sample)))) (+ (abs (- (get-red color 2) (get-red sample))) (abs (- (get-blue color 2) (get-blue sample))) (abs (- (get-green color 2) (get-green sample)))) )) 24 January 2003 CS 200 Spring 2003 29

(+ (abs (- (get-red color 1) (get-red sample))) (abs (- (get-blue color 1) (get-blue sample))) (abs (- (get-green color 1) (get-green sample)))) (define (closer-color? sample color 1 color 2) (< (+ (abs (- (get-red color 2) (get-red sample))) (abs (- (get-blue color 2) (get-blue sample))) (abs (- (get-green color 2) (get-green sample)))) )) 24 January 2003 CS 200 Spring 2003 30

(lambda ( ) (+ (abs (- (get-red color 1 ) (get-red sample ))) (abs (- (get-blue color 1) (get-blue sample ))) (abs (- (get-green color 1) (get-green sample)))) (define (closer-color? sample color 1 color 2) (< (+ (abs (- (get-red color 2) (get-red sample))) (abs (- (get-blue color 2) (get-blue sample))) (abs (- (get-green color 2) (get-green sample)))) )) 24 January 2003 CS 200 Spring 2003 31

(define color-difference (lambda (colora colorb) (+ (abs (- (get-red colora ) (get-red colorb ))) (abs (- (get-blue colora) (get-blue colorb ))) (abs (- (get-green colora) (get-green colorb )))) )) (define (closer-color? sample color 1 color 2) (< (color-difference color 1 sample) (+ (color-difference (abs (- (get-redcolor 2) (get-red sample))) sample) (abs (- (get-blue color 2) (get-blue sample))) (abs (- (get-green color 2) (get-green sample)))) )) 24 January 2003 CS 200 Spring 2003 32

(define color-difference (lambda (colora colorb) (+ (abs (- (get-red colora) (get-red colorb))) (abs (- (get-green colora) (get-green colorb))) (abs (- (get-blue colora) (get-blue colorb)))))) (define (closer-color? sample color 1 color 2) (< (color-difference color 1 sample) (color-difference color 2 sample))) What if you want to use square instead of abs? 24 January 2003 CS 200 Spring 2003 33

(define color-difference (lambda (cf) (lambda (colora colorb) (+ (cf (- (get-red colora) (get-red colorb))) (cf (- (get-green colora) (get-green colorb))) (cf (- (get-blue colora) (get-blue colorb))))))) (define (closer-color? sample color 1 color 2) (< (color-difference color 1 sample) (color-difference color 2 sample))) 24 January 2003 CS 200 Spring 2003 34

(define color-difference (lambda (cf) (lambda (colora colorb) (+ (cf (- (get-red colora) (get-red colorb)) (cf (- (get-green colora) (get-green colorb)) (cf (- (get-blue colora) (get-blue colorb)))) (define (closer-color? sample color 1 color 2) (< ((color-difference square) color 1 sample) ((color-difference square) color 2 sample))) 24 January 2003 CS 200 Spring 2003 35

The Patented RGB RMS Method /* /* /* This is a variation of RGB RMS error. The final square-root has been eliminated to */ speed up the process. We can do this because we only care about relative error. */ HSV RMS error or other matching systems could be used here, as long as the goal of */ finding source images that are visually similar to the portion of the target image */ under consideration is met. */ for(i = 0; i > size; i++) { rt = (int) ((unsigned char)rmas[i] - (unsigned char)image->r[i]); gt = (int) ((unsigned char)gmas[i] - (unsigned char) image->g[i]; bt = (int) ((unsigned char)bmas[i] - (unsigned char)image->b[i]; result += (rt*rt+gt*gt+bt*bt); } 24 January 2003 Your code should never look like this! Use new lines and indenting to make it easy to understand the structure of your code! (Note: unless CS 200 Spring you 2003 are writing a patent. Then the 36 goal is to make it as hard to understand as possible. )

The Patented RGB RMS Method rt = rmas[i] - image->r[i]; gt = gmas[i] - image->g[i]; bt = bmas[i] - image->b[i]; result += (rt*rt + gt*gt + bt*bt); Patent requirements: 1. new – must not be previously available (ancient Babylonians made mosaics) 2. useful 3. nonobvious about ¼ of the class came up with this method! (most of rest used abs instead, which works as well) 24 January 2003 CS 200 Spring 2003 37

PS 1 Grading Scale Gold Star – Excellent Work. You got everything I wanted on this PS. Green Star – Good Work. You got most things on this PS, but some answers could be better. Silver Star – Some problems. Make sure you understand the solutions on today’s slides. PS 1 Average: 24 January 2003 CS 200 Spring 2003 38

No upper limit - Double Gold Star: exceptional work! Better than I expected anyone would do. - Triple Gold Star: Better than I thought possible (deserving of a patent!) - Quadruple Gold Star: You have broken important new ground in CS which should be published in a major journal - Quintuple Gold Star: You deserve to win a Turing Award! (e. g. , a fast, general way to make the best nonrepeating photomosaic) 24 January 2003 CS 200 Spring 2003 39

Problem Set 2 • Unlike PS 1, you should be able to understand all the provided code (except, don’t worry about the trigonometry) • Main ideas: recursion, procedures – We have covered everything you need after today • As we progress, problem sets will expect you to write more code on your own. • PS 8 is “Do something worthwhile using things you have learned from this class. ” (But will be a little bit more specific about what is expected. ) 24 January 2003 CS 200 Spring 2003 40

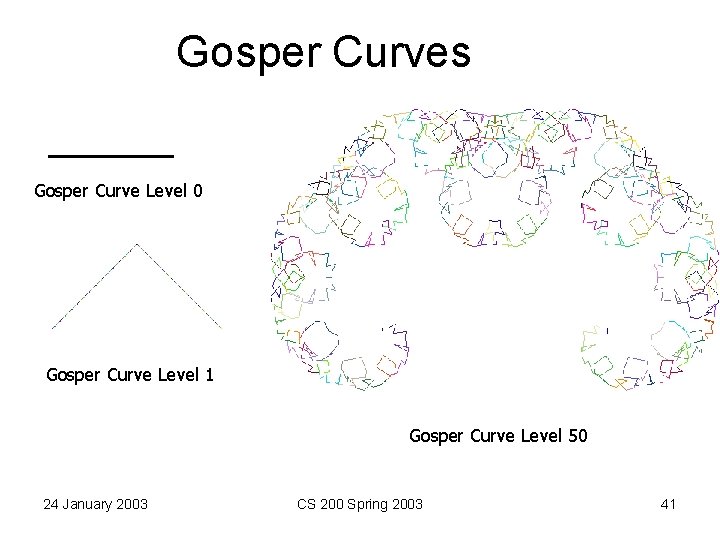
Gosper Curves Gosper Curve Level 0 Gosper Curve Level 1 Gosper Curve Level 50 24 January 2003 CS 200 Spring 2003 41

> (show-gosper smiley 0) > (show-gosper smiley 7) Curves are functions. We can transform them to make new curves. 24 January 2003 CS 200 Spring 2003 42

Charge • Many, many important problems can be solved by recursive definitions • Read GEB Chapter 5 before Monday’s class: lots of great stuff in there! 24 January 2003 CS 200 Spring 2003 43