Lecture 4 RAM Model Space and Time Complexity

Lecture 4. RAM Model, Space and Time Complexity 1

Recap l l l 2 Time and space tradeoff factors should be focus during designing of algorithms, Performance of algorithm should be measure rather than performance of its implemented program. Switching between CPU and IO circuit should be in mind before writing the instructions of an algorithm.

The RAM Model Random Access Machine (not R. A. Memory) l An idealized notion of how the computer works l – – – l 3 Each "simple" operation (+, -, =, if) takes exactly 1 step. Each memory access takes exactly 1 step Loops and method calls are not simple operations, but depend upon the size of the data and the contents of the method. Measure the run time of an algorithm by counting the number of steps.

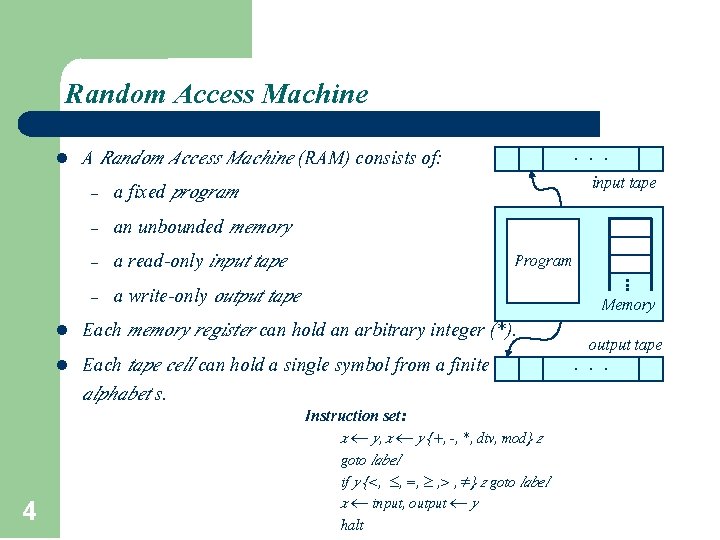
Random Access Machine. . . A Random Access Machine (RAM) consists of: input tape – a fixed program – an unbounded memory Program – a read-only input tape – a write-only output tape Memory Each memory register can hold an arbitrary integer (*). output tape. . . Each tape cell can hold a single symbol from a finite alphabet s. . l l l 4 Instruction set: x y, x y {+, -, *, div, mod} z goto label if y {<, , =, , > , } z goto label x input, output y halt

Space Complexity l 5 The amount of memory required by an algorithm to run to completion – The term memory leaks refer to the amount of memory required is larger than the memory available on a given system

Space Complexity (Cont !!!) l Fixed part: The size required to store certain data/variables, that is independent of the size of the problem: – l Variable part: Space needed by variables, whose size is dependent on the size of the problem: – 6 Such as int a (2 bytes, float b (4 bytes) etc Dynamic array a[]

Space Complexity (cont’d) l S(P) = c + S(instance characteristics) – c = constant l Example: void float sum (float* a, int n) { float s = 0; for(int i = 0; i<n; i++) { s+ = a[i]; } return s; } Constant Space: one for n, one for a [passed by reference!], one for s, one for I , constant space=c=4 7

Running Time of Algorithms l Running time – – l 8 depends on input size n l size of an array l polynomial degree l # of elements in a matrix l # of bits in the binary representation of the input l vertices and edges in a graph number of primitive operations performed Primitive operation – unit of operation that can be identified in the pseudo-code

Steps To determine Time Complexity Step-1. Determine how you will measure input size. Ex: – N items in a list – N x M table (with N rows and M columns) – Two numbers of length N Step-2. Choose the type of operation (or perhaps two operations) – Comparisons – Swaps – Copies – Additions 9 Note: Normally we don't count operations in input/output.

Steps To determine Time Complexity (Cont !!!) Step-3. Decide whether you wish to count operations in the – – – Best case? - the fewest possible operations Worst case? - the most possible operations Average case? This is harder as it is not always clear what is meant by an "average case". Normally calculating this case requires some higher mathematics such as probability theory. Step-4. For the algorithm and the chosen case (best, worst, average), express the count as a function of the input size of the problem. 10

Steps To determine Time Complexity (Cont !!!) 5. Given the formula that you have determined, decide the complexity class of the algorithm. Q. What is the complexity class of an algorithm? A. a complexity class is a set of problems of related resource-based complexity, such as P, NP classes Q. Is there really much difference between 3 n 5 n + 20 and 6 n -3 11 A. Yes but when n is large?

Primitive Operations in an algorithm l l l l 12 Assign a value to a variable (i. e. a=5) Call a method (i. e. method()) Arithmetic operation (i. e. a*b, a-b*c) Comparing two numbers ( i. e. a<=b, a>b &&a>c) Indexing into an array (i. e. a[0]=5) Following an object reference (i. e. Test obj) Returning from a method (i. e. return I )

Assignment Statement l l The running time of a an assignment is considered as constant Examples: – – – 13 A=5; A[5]=7 C=a+b; Note: - Running time of assignments can be considered as 1 or C (Refer to constant values)

for Loops The running time of a for loop is at most the running time of the statements inside the for loop (including tests) times the number of iterations. Example Let 1. running time of basic operations For(i=0; i<=n-1; i++) is constant C A[i]=0; l 14 Note: (number of basic steps in loop body) * (number of iterations) 2. and loop is iterated n times then Total Running time will be n*c

Nested for Loops l l 15 The total running time of a statement inside a group of nested for loops is the running time of the statement multiplied by the product of the sizes of all the for loops. Example Let 1. running time of basic operations for(i=0; i<=n-1; i++) is constant C for(j=0; j<=m-1; j++) 2. Running time of outer loop (i. e. K++; i) is n 3. And running time of Inner loop (i. e. j) is m 4. Total Running time will be m*n*c

Consecutives for Loops l l 16 The total running time of consecutive loops is the sum of running of all consecutives loops Example for(i=0; i<=n-1; i++) Let 1. running time of basic operations K++; is constant C for(j=0; j<=m-1; j++) 2. Running time of loop (i. e. i) is n 3. And running time of loop (i. e. j) K++; is m 4. Total Running time will be n*c + m * c

Conditional Statements l l The running time of an if-else statement is never more than the running time of the test plus the larger of the running times of S 1 and S 2. Let 1. Condition is true and path have Example one basic operation (i. e. S 1) then if(Condition) Ruining time will be constant C 1 S 1; 2. Similarly, if condition is false and path have one basic else operation (i. e. S 2) then Ruining S 2; time will be constant C 2 Note: Number of basic steps on branch 17 that is executed

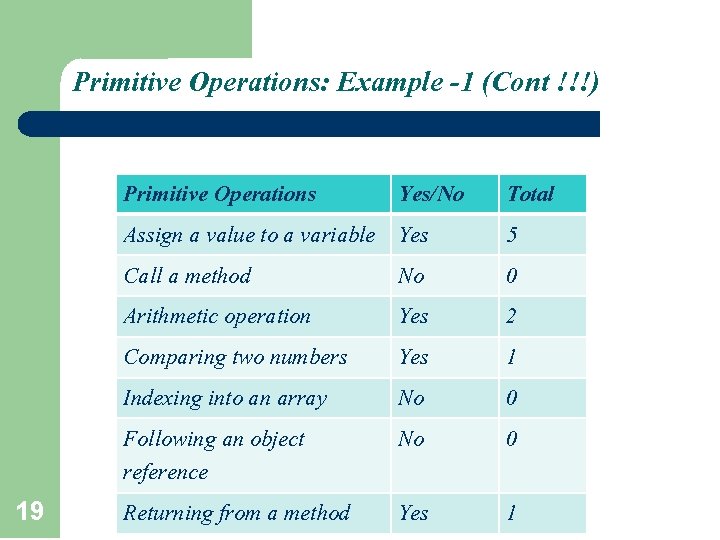
Primitive Operations: Example -1 l Count the number of primitive operations in this program : Int method() { i = 0; a = 0; for (i=1; i<=n; i++) { printf(“%d”, i); a=a+i; } return I } 18 Primitive Operations Assign a value to a variable Call a method Arithmetic operation Comparing two numbers Indexing into an array Following an object reference Returning from a method Yes/No Total

Primitive Operations: Example -1 (Cont !!!) 19 Primitive Operations Assign a value to a variable Call a method Arithmetic operation Comparing two numbers Indexing into an array Following an object reference Returning from a method Yes/No Yes Yes No No Total 5 0 2 1 0 0 Yes 1

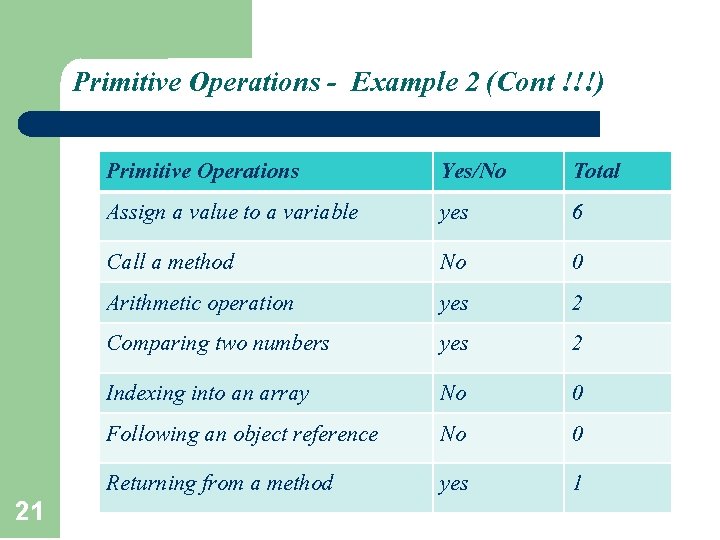
Primitive Operations - Example 2 l Count the number of primitive operations in this program : Int method() { i = 0; a = 0; for (i=1; i<=n; i++) { printf(“%d”, i); for (a=1; a<=n; a++) printf(“%d”, a); } return I } 20 Primitive Operations Assign a value to a variable Call a method Arithmetic operation Comparing two numbers Indexing into an array Following an object reference Returning from a method Yes/No Total

Primitive Operations - Example 2 (Cont !!!) 21 Primitive Operations Assign a value to a variable Yes/No yes Total 6 Call a method Arithmetic operation Comparing two numbers No yes 0 2 2 Indexing into an array Following an object reference No No 0 0 Returning from a method yes 1

Summary RAM model is used to measure the run time of an algorithm by counting the number of steps. l Space complexity of an algorithm refer to the amount of memory required to run. l Time complexity of an algorithm refer to its running time, which depends on input size. l Primitive operations refer to the unit of operation that can be identified in the pseudo-code l 22

In Next Lecturer l 23 In next lecture, we will talk about the types of algorithm complexity and how to find running time of different pseudo codes.