Lecture 4 part 1 Linear Regression Analysis Two

Lecture 4, part 1: Linear Regression Analysis: Two Advanced Topics Karen Bandeen-Roche, Ph. D Department of Biostatistics Johns Hopkins University July 14, 2011 Introduction to Statistical Measurement and Modeling

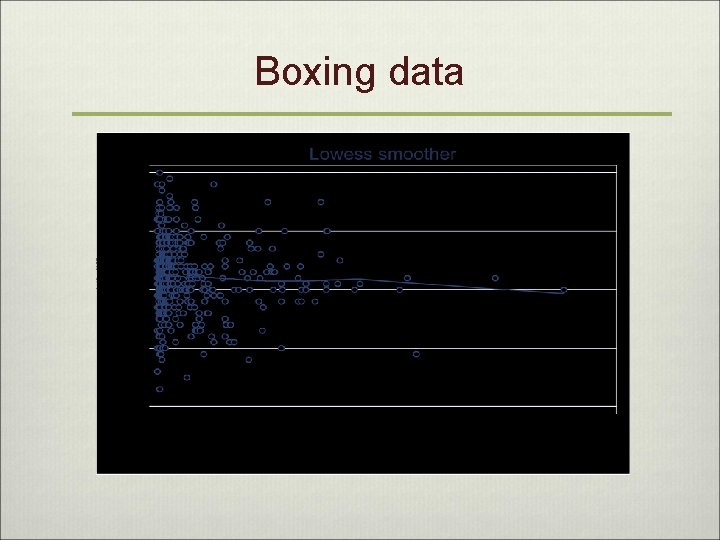
Data examples v Boxing and neurological injury v Scientific question: Does amateur boxing lead to decline in neurological performance? v Some related statistical questions: v Is there a dose-response increase in the rate of cognitive decline with increased boxing exposure? v Is boxing-associated decline independent of initial cognition and age? v Is there a threshold of boxing that initiates harm?

Boxing data

Outline v Topic #1: Confounding v Handling this is crucial if we are to draw correct conclusions about risk factors v Topic #2: Signal / noise decomposition v Signal: Regression model predictions v Noise: Residual variation v Another way of approaching inference, precision of prediction

Topic # 1: Confounding v Confound means to “confuse” v When the comparison is between groups that are otherwise not similar in ways that affect the outcome v Lurking variables, ….

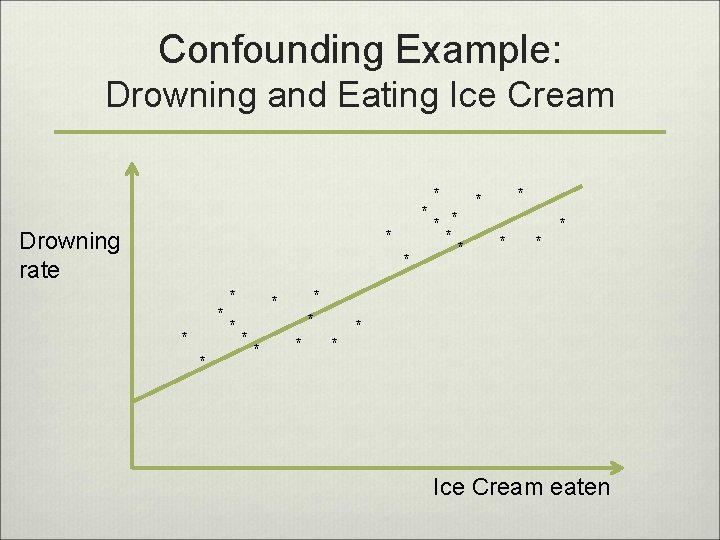
Confounding Example: Drowning and Eating Ice Cream * * Drowning rate * * * * * * Ice Cream eaten

Confounding Epidemiology definition: A characteristic “C” is a confounder if it is associated (related) with both the outcome (Y: drowning) and the risk factor (X: ice cream) and is not causally in between Ice Cream Consumption Drowning rate ? ? July 2010 JHU Intro to Clinical Research 7

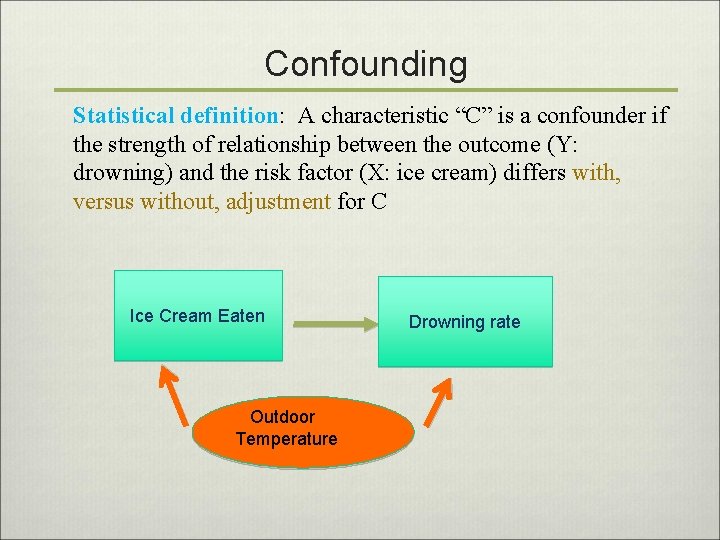
Confounding Statistical definition: A characteristic “C” is a confounder if the strength of relationship between the outcome (Y: drowning) and the risk factor (X: ice cream) differs with, versus without, adjustment for C Ice Cream Eaten Outdoor Temperature Drowning rate

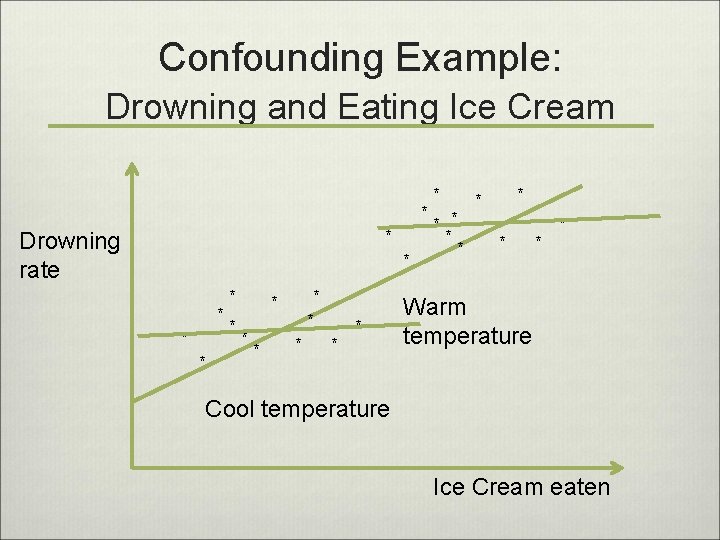
Confounding Example: Drowning and Eating Ice Cream * * Drowning rate * * * * * * Warm temperature Cool temperature Ice Cream eaten

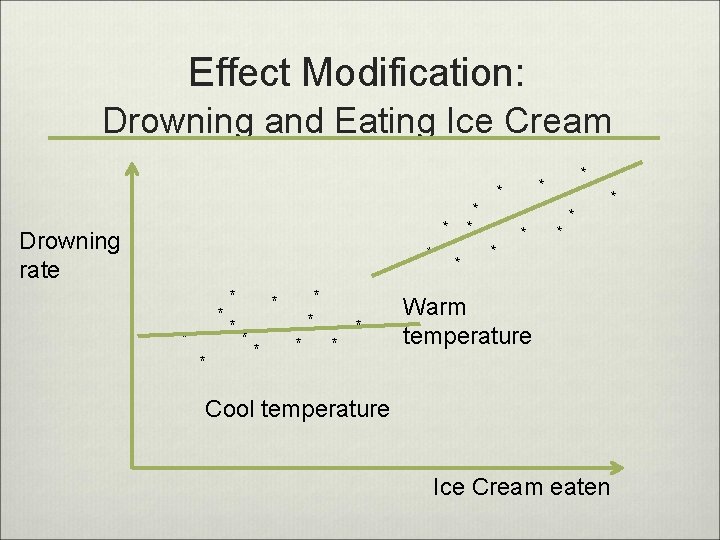
Effect modification A characteristic “E” is an effect modifier if the strength of relationship between the outcome (Y: drowning) and the risk factor (X: ice cream) differs within levels of E Ice Cream Consumption Drowning rate Outdoor temperature July 2010 JHU Intro to Clinical Research 10

Effect Modification: * * * Drowning rate * * * * Drowning and Eating Ice Cream * * * * Warm temperature Cool temperature Ice Cream eaten

Topic #2: Signal/Noise Decomposition v Lovely due to geometry of least squares v Facilitates testing involving multiple parameters at once v Provides insight into R-squared

Signal/Noise Decomposition v First step: decomposition of variance v “Regression” part: Variance of s v “Error” or “Residual” part: Variance of e v Together: These determine “total” variance of Ys v “Sums of Squares” (SS) rather than variance per se v Regression SS (SSR): v Error SS (SSE): v Total SS (SST):

Signal/Noise Decomposition v Properties v SST = SSR + SSE v SSR/SST = “proportion of variance explained” by regression = R-squared v Follows from geometry v SSR and SSE are independent (assuming A 1 -A 5) and have easily characterized probability distributions v Provides convenient testing methods v Follows from geometry plus assumptions

Signal/Noise Decomposition v SSR and SSE are independent v Define M = span(X) and take “Y” as centered at v It is possible to orthogonally rotate the coordinate axes so that first p axes ε M; remaining n-p-1 axes ε M⊥ v Gram-Schmidt orthogonalization v Doing this transforms Y into TY : =Z, for some orthonormal matrix T with columns: = {e 1, . . . , en-1} v Distribution of Z = N(TE[Y|X], σ2 I)

Signal/Noise Decomposition v SSR and SSE are independent - continued v TY=Z Y = T’Z v SSE = squared length of = v SSR = squared length of = v Claim now follows: SSR & SSE are independent because (Z 1, …, Zp) and (Zp+1, …, Zn-1) are independent

Signal/Noise Decomposition v Under A 1 -A 5 SSE, SSR and their scaled ratio have convenient distributions v Under A 1 -A 2: E[Y|X] ε M, E[Zj|X] =0, all j>p v Recall {Z 1, . . . , Zn-1} are mutually independent normal with variance=σ2 v Thus SSE = = ~ σ2 χ2 n-p-1 under A 1 -A 5 (a sum of k independent squared N(0, 1) is )

Signal/Noise Decomposition v Under A 1 -A 5 SSE, SSR and their scaled ratio have convenient distributions v For j ≤ p E[Zj|X] ≠ 0 in general v Exception: H 0: β 1=…=βp = 0 v Then SSR = ~ σ2 χ2 p under A 1 -A 5 and ~ F p, n-p-1 ~ with numerator and denominator independent.

Signal/Noise Decomposition v An organizational tool: The analysis of variance (ANOVA) table SOURCE Sum of Squares (SS) Degrees of freedom (df) Mean square (SS/df) Regression SSR p SSR/p Error SSE n-p-1 SSE/(n-p-1) = Total SST = SSR + SSE n-1 F= MSR/MSE

“Global” hypothesis tests v These involve sets of parameters v Hypotheses of the form H 0: βj = 0 for all j in a defined subset of {j=1, . . . , p} vs. H 1: βj ≠ 0 for at least one of the j Example 1: H 0: βLATITUDE = 0 and βLONGITUDE = 0 Example 2: H 0: all polynomial or spline coefficients involving a given variable = 0. Example 3: H 0: all coefficients involving a variable = 0.

“Global” hypothesis tests v Testing method: Sequential decomposition of sums of squares v Hypothesis to be tested is H 0: βj 1=. . . =βjk = 0 in full model v Fit model excluding xj 1, . . . , xjpj: Save SSE = SSEs v Fit “full” (or larger) model adding xj 1, . . . , xjpj to smaller model. Save SSE=SSEL, often=overall SSE v Test statistic S = [(SSES-SSEL)/pj]/[SSEL(n-p-1)] v Distribution under null: F(pj, n-p-1) v Define rejection region based on this distribution v Compute S v Reject or not as S is in rejection region or not

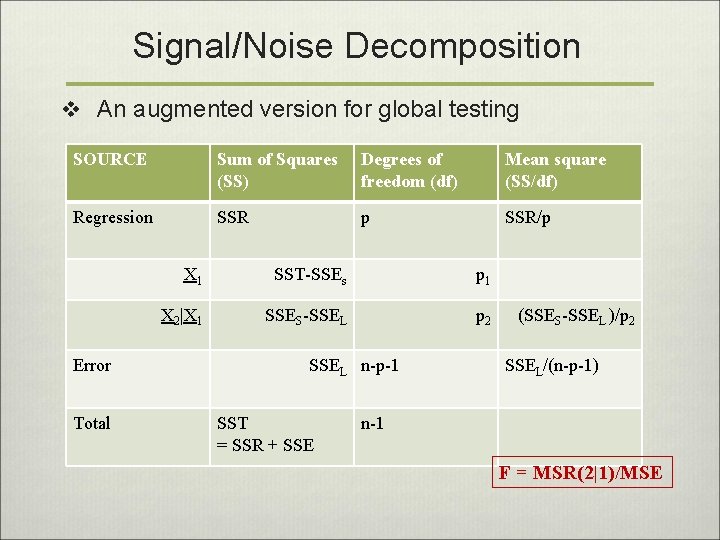
Signal/Noise Decomposition v An augmented version for global testing SOURCE Sum of Squares (SS) Degrees of freedom (df) Mean square (SS/df) Regression SSR p SSR/p Error Total X 1 SST-SSEs p 1 X 2|X 1 SSES-SSEL p 2 SSEL n-p-1 SST = SSR + SSE (SSES-SSEL )/p 2 SSEL/(n-p-1) n-1 F = MSR(2|1)/MSE

R-squared – Another view v From last lecture: ECDF Corr(Y, ) squared v More conventional: R 2 = SSR/SST v Geometry justifies why they are the same v Cov(Y, ) = Cov(Y- + , ) = Cov(e, ) + Var( ) v Covariance = inner product first term = 0 v A measure of precision with which regression model describes individual responses

Outline: A few more topics v Colinearity v Overfitting v Influence v Mediation v Multiple comparisons

Main points v Confounding occurs when an apparent association between a predictor and outcome reflects the association of each with a third variable v A primary goal of regression is to “adjust” for confounding v Least squares decomposition of Y into fit and residual provides an appealing statistical testing framework v An association of an outcome with predictors is evidenced if SS due to regression is large relative to SSE v Geometry: orthogonal decomposition provides convenient sampling distribution, view of R 2 v ANOVA